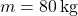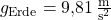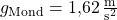Gewichtskraft
Was ist die Gewichtskraft, wie lautet ihre Formel und wo liegt der Unterschied zwischen Gewichtskraft und Masse? Das erfährst du im Video und in unserem Beitrag!
Was ist Gewichtskraft?
Die Gewichtskraft gibt an, wie stark ein Körper nach unten drückt oder gezogen wird. Sie kann mit der Formel Fg = m · g berechnet werden und hat eine bestimmte Stärke und eine Richtung.
Wie stark genau die Gewichtskraft ist, hängt dabei von der Masse m ab. Du kannst dir merken: je mehr Masse ein Körper hat, desto größer ist seine Gewichtskraft. Aber auch der Ortsfaktor g hat einen Einfluss. Je nachdem, wo du dich auf unserer Erde befindest, ist die Gewichtskraft nämlich unterschiedlich stark.
Die Richtung, in die die Gewichtskraft wirkt, ist dagegen immer dieselbe. Denn du und alles um dich herum werden Richtung Erdmittelpunkt gedrückt, beziehungsweise gezogen. Die Kraft gibt also an, wie stark du zum Beispiel auf dem Boden drückst und sie ist der Grund, warum du beim Trampolin springen wieder nach unten kommst.
Gewichtskraft Formel
Um die Gewichtskraft zu berechnen, nimmst du die Masse m eines Körpers mal den Ortsfaktor g:
![\[F_{\text{G}}=\textcolor{magenta}{m}\cdot\textcolor{blue}{g}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-473576fd3925654d73f48e362d11577b_l3.png "Rendered by QuickLaTeX.com")
- Fg = Gewichtskraft
- m = Masse
- g = Ortsfaktor
In der Formel kannst du sehen, dass die entscheidenden Größen zur Berechnung die Masse m und der Ortsfaktor g sind.
Die Masse m eines bestimmten Körpers ist überall gleich. Egal ob du sie am Äquator oder am Nordpol misst, ein Kilogramm bleibt ein Kilogramm. Außerdem kannst du aus der Formel ableiten, dass je mehr Masse ein Körper hat, desto mehr Kraft ist nötig, um ihn zu beschleunigen.
Wie dir der Name schon sagt, ist der Ortsfaktor g vom Ort abhängig. Für unsere Erde gehst du jedoch von durchschnittlich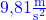 
aus und kannst zum Ortsfaktor auch Fallbeschleunigung sagen.
Gewichtskraft Einheit
Um die Gewichtskraft zu berechnen, multiplizierst du zwei Größen miteinander:
![\[F_{\text{G}}=m\cdot g\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-37dbd438b5e8eaabca002113c6191393_l3.png "Rendered by QuickLaTeX.com")
- Die Masse m in
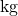. - Den Ortsfaktor g in
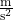oder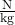 
. Beides sagt das Gleiche aus, welche Einheit du verwendest, bleibt also dir überlassen.
Dadurch ergibt sich die Einheit Newton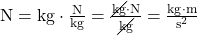 
Merke: Die Einheit der Gewichtskraft ist Newton N. Um einen Körper mit der Masse von einem kg um einen m/s2 zu beschleunigen, braucht man ein Newton N.
Ortsabhängigkeit der Gewichtskraft
Obwohl du von einem durchschnittlichen Ortsfaktor von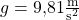 
ausgehst, ist er überall auf unserer Erde ein kleines bisschen unterschiedlich — je nachdem wo du dich genau befindest. Am Äquator beträgt er zum Beispiel 
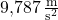. An den Polen ist der Ortsfaktor mit 
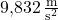etwas stärker.
Das liegt daran, dass unsere Erde ein bisschen ‚breiter‘ als ‚hoch‘ ist. Je weiter du vom Erdmittelpunkt entfernt bist, desto schwächer ist also der Ortsfaktor. Das gleiche gilt übrigens auch für sehr hohe Berge wie zum Beispiel den Mount Everest mit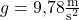 
.
Diese Unterschiede treten jedoch nicht nur auf unserem Planeten auf. Verschiedene Himmelskörper haben nämlich ganz unterschiedliche Ortsfaktoren.
Ortsfaktor Mond:
Zum Beispiel beträgt der Ortsfaktor auf dem Mond 1,62 m/s2. Damit ist er um einiges geringer als der Ortsfaktor der Erde. Ein Körper mit der Masse 6 kg ist deshalb auf dem Mond genauso schwer wie ein Körper mit 1 kg auf der Erde.
Gewichtskraft berechnen
Nun haben wir die nötigen Grundlagen, um die Gewichtskraft berechnen zu können. Betrachten wir dazu ein kleines Beispiel:
Neil Armstrong, der erste Mensch auf dem Mond, hatte eine Masse von 80 kg. Welche Gewichtskraft hatte der berühmte Astronaut auf der Erde und welche Kraft übte er aus, als er den Mond betrat? Das kannst du ganz einfach mit der Formel der Gewichtskraft berechnen.
1.) Für die Berechnung auf der Erde sind folgende Angaben gegeben:
Setzt du die gegebene Masse m und Erdbeschleunigung g in die Formel ein, kannst du die Gewichtskraft des Astronauten berechnen:
![\[ \Rightarrow F_{\text{g,}\text{Erde}}=m\cdot g_{\text{Erde}}=80\,\text{kg}\cdot9,81\,\frac {\text{m}}{\text{s}^{2}}=784,8\,\frac{\text{kg}\cdot\text{m}}{\text{s}^{2}}}=784,8\,\text{N}.\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-ed6b6b60667ffe3bb5743e254b8c6b9d_l3.png "Rendered by QuickLaTeX.com")
2.) Für die Berechnung auf dem Mond sind folgende Angaben gegeben:
![\[ \Rightarrow F_{\text{g,}\text{Mond}}=m\cdot g_{\text{Mond}}=80\text{kg}\cdot1,62\frac{\text{m}}{\text{s}^{2}}=129,6\frac{\text{kg}\cdot\text{m}}{\text{s}^{2}}=129,6\ \text{N}.\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-83247c83e0bb872b10ed9517e9d98cbb_l3.png "Rendered by QuickLaTeX.com")
Du siehst also, inwiefern die Gewichtskraft ortsabhängig ist. Obwohl die Masse des Astronauten auf beiden Planeten identisch war, übte er in Abhängigkeit der Fallbeschleunigung bzw. des Ortsfaktors verschiedene Kräfte aus. Dadurch konnte Neil Armstrong auf dem Mond nicht nur höher springen als auf der Erde, es dauerte auch länger, bis er wieder auf dem Boden angekommen ist.
Masse und Gewichtskraft
In der Alltagssprache verwenden wir oft die Ausdrücke Gewicht und Masse als Synonyme. Physikalisch gesehen handelt es sich aber um sehr unterschiedliche Begriffe.
- Die Masse ist eine Eigenschaft eines Körpers. Außerdem ist die Masse eines Körpers überall gleich groß.
- Das Gewicht beschreibt die Wechselwirkung zwischen zwei Körpern. Die Gewichtskraft kann deshalb als Ergebnis aus dem jeweiligen Ortsfaktor und der Masse eines Körpers betrachtet werden. So hat beispielsweise der Ortsfaktor von einem bestimmten Himmelskörper einen Einfluss auf die Gewichtskraft eines Menschen.
Gravitationsgesetz
Wie du nun gelernt hast, kommt die Gewichtskraft aufgrund der Massenanziehung zustande. Diese Anziehung kannst du übrigens auch als Gravitation bezeichnen.
Aber wie kannst du die Gravitation zwischen zwei Körpern, zum Beispiel zwischen Erde und Mond berechnen? Schau dir unser Video zum Gravitationsgesetz an und finde es heraus!
