Erwartungswert
In diesem Artikel erklären wir dir, was der Erwartungswert ist und wie du ihn berechnen kannst.
Mit unserem Video verstehst du das Thema noch schneller, schau doch mal rein!
Inhaltsübersicht
Erwartungswert einfach erklärt
Stell‘ dir vor, du wirfst einen Würfel unendlich oft und berechnest anschließend den Mittelwert all deiner Würfe. Das Ergebnis dieser Berechnung ist der sogenannte Erwartungswert (griechisch µ („mü“)).
Der Erwartungswert ist der Mittelwert, wenn du ein Zufallsexperiment unendlich oft wiederholst. Er gibt an, mit welchem Wert du auf lange Sicht bei deinem Zufallsexperiment rechnen kannst. Bei einem Würfelwurf sagt dir der Erwartungswert also zum Beispiel, welche Augenzahl du langfristig durchschnittlich erwarten kannst, wenn du unendlich oft würfelst.
Berechnen kannst du den Erwartungswert, indem du die Ausprägung der Zufallsvariable mit der entsprechenden Wahrscheinlichkeit multiplizierst. Anschließend summierst du alles auf.
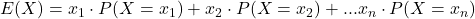
 – Erwartungswert von X
– Erwartungswert von X
 – erste Ausprägung der Zufallsvariable X (z.B. Augenzahl „1“)
– erste Ausprägung der Zufallsvariable X (z.B. Augenzahl „1“)
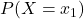 – Wahrscheinlichkeit der ersten Ausprägung (z.B.
– Wahrscheinlichkeit der ersten Ausprägung (z.B. 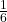 )
)
Mit dem Erwartungswert kannst du zum Beispiel prüfen, ob ein Spiel „fair“ ist. In einem fairen Spiel müssten sich Gewinn und Verlust auf lange Sicht ausgleichen. Folglich hat ein faires Spiel einen Erwartungswert von 0.
Erwartungswert berechnen
Bei der Berechnung solltest du den Erwartungswert nicht mit dem arithmetischen Mittel verwechseln. Das arithmetische Mittel bezieht sich auf eine konkret beobachtete Anzahl an Durchgängen deines Zufallsexperiments, von denen du den Mittelwert bestimmst. Der Erwartungswert bezieht sich hingegen auf eine unendliche Zahl an Durchgängen und gibt den theoretischen Wert an, den du langfristig erwarten kannst.
Das folgende Beispiel verdeutlicht den Unterschied zwischen der Berechnung des Erwartungswerts und des arithmetischen Mittels:
Ein Zufallsgenerator gibt mit jeweils gleicher Wahrscheinlichkeit den Wert 0 oder 1 aus.
Der Erwartungswert µ beträgt 0,5. Um diesen zu erhalten, multiplizierst du die Ausprägung der Zufallsgröße mit der entsprechenden Wahrscheinlichkeit und summierst alles.
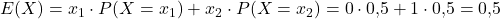
Das arithmetische Mittel wird bei einer kleinen Anzahl an Wiederholungen vom Erwartungswert abweichen. Wenn du bei 5 Wiederholungen beispielsweise die Ausprägung „0,1,0,0,1” erhältst, ergibt sich 0,4 als arithmetisches Mittel. Du summierst hier alle Werte und dividierst durch die Anzahl.
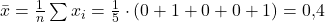
Bei 20 Wiederholungen erhältst du dann zum Beispiel 11 mal eine 0 und 9 mal eine 1, dies ergibt ein arithmetisches Mittel von 0,45.
Du siehst also, umso größer die Anzahl der Durchgänge des Zufallsexperiment wird, desto näher rückt der Mittelwert an den Erwartungswert. Diese Beobachtung wird auch als Gesetz der großen Zahlen bezeichnet.
Die Wahrscheinlichkeit des Zufallsgenerators war hier für alle möglichen Ergebnisse gleich. Ändert sich die Wahrscheinlichkeit jedoch, berechnet man den Erwartungswert als gewichtetes arithmetisches Mittel. Dazu setzt du einfach die entsprechenden Wahrscheinlichkeiten der Ausprägungen in die Formel ein.
Formel
Die Berechnung des Erwartungswertes erfolgt für diskrete Verteilungen und für stetige Verteilungen auf unterschiedliche Art und Weise. Eine diskreten Zufallsvariable nimmt eine abzählbare Menge an Ergebnissen an (Beispiel: Würfel), eine stetige Zufallsvariable nimmt hingegen unendlich viele, nicht abzählbare Werte an (Beispiel: Temperatur).
Der Erwartungswert ist die Zahl, die deine Zufallsgröße X (z.B. Augenzahl eines Würfels) im Durchschnitt annimmt (Mittelwert). Um den Erwartungswert zu berechnen, multiplizierst du jede Zahl xi von X (hier: 1 bis 6) mit ihrer Wahrscheinlichkeit P(X=xi) (hier: 1/6) und addierst all deine Ergebnisse.
Diskrete Zufallsvariable
Mit der folgenden Formel kannst du den Erwartungswert µ bei einer diskret verteilten Zufallsvariable X berechnen.
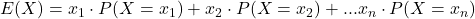
Beispiel Würfel: Du möchtest den Erwartungswert eines 6-seitigen Würfels bestimmen. Die Ausprägungen der Zufallsvariable X sind also die 6 Seiten eines Würfels.
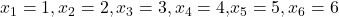
Alle Ausprägungen haben die gleiche Wahrscheinlichkeit. Es handelt sich also um ein Laplace Experiment :
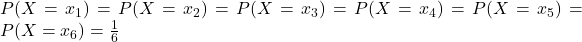
Jetzt müssen wir die Werte nur noch in die Formel bei diskreten Verteilungen einsetzen und erhalten für den Erwartungswert:
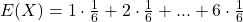
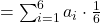
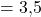
Auf lange Sicht kannst du also im Durchschnitt ein Ergebnis von 3,5 erwarten.
Stetige Zufallsvariable
Um den Erwartungswert einer stetigen Zufallsvariablen zu berechnen, musst du das Integral bilden. Die Grenzen des Integrals hängen davon ab, wie die stetig verteilte Zufallsvariable definiert ist.
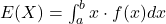
Beispiel Temperatur: Die Temperatur in einem Kühlhaus kann zwischen 0 und 4 Grad Celsius variieren. Diese Temperaturschwankungen sind durch folgende Dichtefunktion gegeben (x ist in Grad Celsius angegeben).
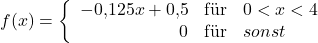
Setzt du die Werte in die Formel ein, kommst du auf folgendes Ergebnis:
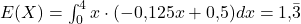
Das heißt, die zu erwartende Temperatur liegt im Schnitt bei ca. 1,3 Grad Celsius.
Wahrscheinlichkeitsverteilung
Für die meisten konkreten Berechnungen ist eine vollständige Beschreibung der Wahrscheinlichkeitsverteilung gar nicht nötig. Einen guten Überblick über die Verteilung liefern dir auch die charakteristische Maßzahlen wie die Varianz und Standardabweichung oder eben der Erwartungswert.
Im Folgenden siehst du eine Auflistung der wichtigsten Wahrscheinlichkeitsverteilungen wie zum Beispiel der Normalverteilung , oder der Binomialverteilung mit deren Erwartungswerten.
| Dichte | Erwartungswert | |
| Bernoulliverteilung | 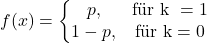 |
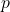 |
| Binomialverteilung | 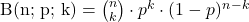 |
 |
| Normalverteilung | 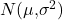 |
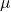 |
| Exponentialverteilung | 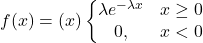 |
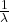 |
Rechenregeln
Außerdem solltest du die drei folgenden Rechenregeln auf jeden Fall im Kopf haben:
Regel 1) Der Erwartungswert von Summen zweier unterschiedlicher Zufallsvariablen lässt sich folgendermaßen umformen:
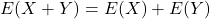
Regel 2) Wenn 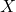 und
und 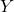 unabhängige Zufallsvariablen sind, kannst du das Produkt zweier Erwartungswerte zusammenfassen bzw. trennen:
unabhängige Zufallsvariablen sind, kannst du das Produkt zweier Erwartungswerte zusammenfassen bzw. trennen:
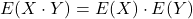
Regel 3) Die lineare Transformation zeigt die Umformung von Erwartungswerten, wenn diese Konstanten enthalten. 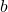 und
und  sind Konstanten und X ist eine unabhängige Zufallsvariable.
sind Konstanten und X ist eine unabhängige Zufallsvariable.
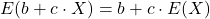
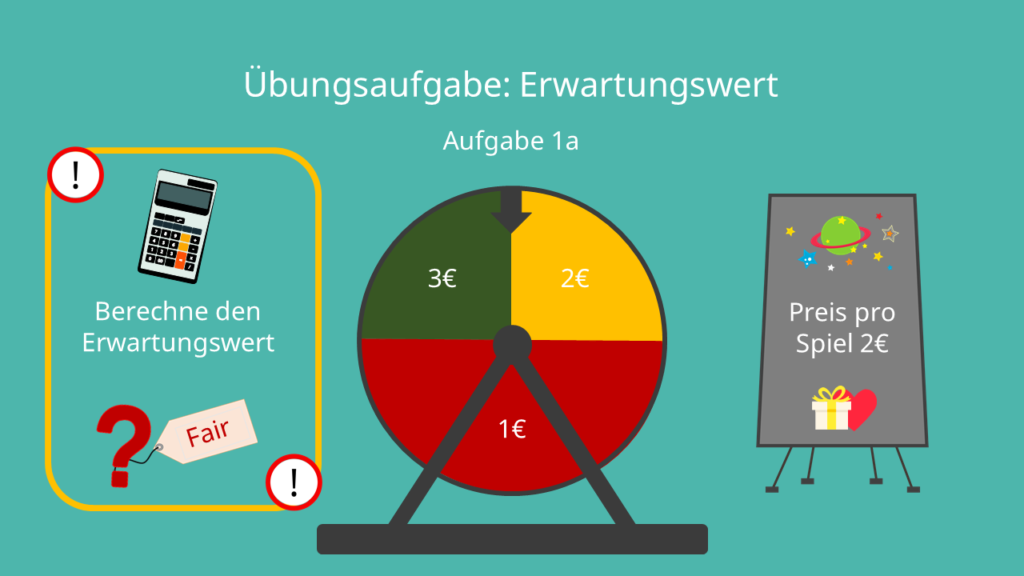
Aufgabe 1: faires Spiel
1a: Du hast folgendes Glücksrad mit 2€ Einsatz gegeben. Berechne den Erwartungswert. Ist das Spiel fair?
Zum Lösungsweg:
Zur Lösung:
1b: Du darfst die Auszahlung im grünen Feld ändern, alle anderen Werte müssen gleich bleiben. Wie hoch müsste die Auszahlung im grünen Feld sein, damit das Spiel fair ist?
Zum Lösungsweg:
Zur Lösung:
Aufgabe 2: Urnenmodell
In einer Urne befinden sich 3 blaue und 6 rote Kugeln, also insgesamt 9 Kugeln. Du ziehst 4 Kugeln ohne diese danach zurückzulegen. Die Reihenfolge ist dir nicht wichtig. Wie viele rote Kugeln wirst du erwartungsgemäß ziehen?
Zum Lösungsweg:
Zur Lösung: