Arithmetisches Mittel
In diesem Beitrag geht es um das arithmetische Mittel. Anhand mehrerer Beispiele werden wir den Mittelwert berechnen. Außerdem zeigen wir die wie man das gewichtete arithmetische Mittel bestimmen kann.
Noch schneller verstehst du das Thema mit unserem Video , schau doch mal rein!
Inhaltsübersicht
Arithmetisches Mittel einfach erklärt
Das arithmetische Mittel (auch „Mittelwert“) ist eine Kennzahl, die dir angibt, wie hoch oder niedrig deine Messwerte im Durchschnitt sind. Für die Berechnung des arithmetischen Mittels musst du einfach alle Messwerte aufaddieren und das Ergebnis durch die Anzahl der Messwerte teilen.
Die Formel zur Berechnung des arithmetischen Mittels sieht so aus:
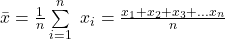
Wenn zum Beispiel Peter, Max und Sophia 80 kg, 75 kg und 55 kg wiegen, dann beträgt das arithmetische Mittel der Gruppe 70 kg. Du hast es erhalten, indem du die Körpergewichte der drei Personen zusammengezählt und das Ergebnis durch die Anzahl der Personen, also durch 3, geteilt hast.
Da das arithmetische Mittel gehört neben dem Modus und dem Median zu den Lagemaßen. Diese drei Kennzahlen geben dir Auskunft darüber, welche Messwerte besonders herausstechen und sie besonders gut beschreiben.
Arithmetisches Mittel berechnen
Sehen wir uns nun die Berechnung des arithmetischen Mittels direkt an einem anschaulichen Beispiel an.
Fünf befreundete Studierende erhalten die folgenden Noten in einer Statistik Klausur:
| Note xi | 2 | 2 | 5 | 3 | 4 |
Mithilfe der oben angeführten Formel lässt sich der arithmetische Mittelwert nun wie folgt bestimmen. Du summierst die Noten der einzelnen Studierenden zunächst auf. Das Ergebnis teilst du durch die Anzahl der Messwerte, in unserem Beispiel also durch 5:
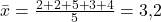
Das Ergebnis ist das arithmetische Mittel. Die Studierenden haben also im Durschnitt eine Note von 3,2 erreicht.
Gewichtetes arithmetisches Mittel
Mit dem Ausdruck gewichtetes arithmetisches Mittel wird eine Variante zur Berechnung des arithmetischen Mittels bezeichnet. Bei dieser auch als gewogenes arithmetisches Mittel bezeichneten Abwandlung werden bestimmte Beobachtungen stärker gewichtet als andere.
Meistens werden die Beobachtungen dabei mit ihrer (relativen) Häufigkeit gewichtet. Das bedeutet, Messwerte, die häufiger vorkommen, werden stärker gewichtet als seltene Messwerte.
In anderen Worten ist das gewichtete arithmetische Mittel einfach nur eine Berechnungsweise des arithmetischen Mittelwerts, wenn bestimmte Messwerte nicht nur einmal, sondern mehrfach vorkommen.
Gewichtetes arithmetisches Mittel: Formel
Das gewichtete arithmetische Mittel lässt sich sowohl mithilfe der absoluten Häufigkeit als auch mit der relativen Häufigkeit berechnen. Daraus ergeben sich die folgenden Formeln zum Berechnen des gewogenen arithmetischen Mittel:
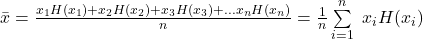
Zur Berechnung des gewogenen Mittels mit Gewichtung durch die absolute Häufigkeit multipliziert man die Beobachtungen mit der absoluten Häufigkeit der Beobachtungen 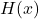 . Du multiplizierst also jeden Messwert mit der Anzahl, wie häufig er vorgekommen ist. Teile anschließend die Summe wieder durch die Anzahl der Beobachtungen. Häufig auftretende Merkmale fallen so im Durchschnitt stärker ins Gewicht.
. Du multiplizierst also jeden Messwert mit der Anzahl, wie häufig er vorgekommen ist. Teile anschließend die Summe wieder durch die Anzahl der Beobachtungen. Häufig auftretende Merkmale fallen so im Durchschnitt stärker ins Gewicht.
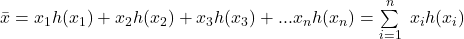
Äquivalent zur Berechnung des gewichteten arithmetischen Mittels mithilfe der absoluten Häufigkeit erfolgt die Berechnung mit der relativen Häufigkeit.
Wieder multiplizierst du die Beobachtungen mit ihrer Häufigkeit, diesmal jedoch mit der relativen Häufigkeit 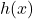 . Da bei den relativen Häufigkeiten bereits durch die Anzahl der Beobachtungen geteilt wurde, musst du das diesmal nicht mehr machen. Nach dem multiplizieren der Beobachtungen mit den relativen Häufigkeiten erhältst du also direkt das arithmetische Mittel.
. Da bei den relativen Häufigkeiten bereits durch die Anzahl der Beobachtungen geteilt wurde, musst du das diesmal nicht mehr machen. Nach dem multiplizieren der Beobachtungen mit den relativen Häufigkeiten erhältst du also direkt das arithmetische Mittel.
Es ist wichtig zu verstehen, dass die absolute und relative Häufigkeit zwar üblicherweise als Mittel zur Gewichtung herangezogen werden, jedoch eine Gewichtung auch nach anderen frei wählbaren Kriterien/Maßstäben erfolgen kann. Das gewichtete arithmetische Mittel kann außerdem verwendet werden, um Problemstellungen zu lösen, die sonst nur mit dem harmonischen Mittel zu lösen sind.
Beispiel (absolute Häufigkeit)
Eine Gruppe von 50 Studierenden schreibt eine Statistik Klausur. Es ergeben sich die in der Häufigkeitstabelle abgetragenen Notengruppen.
| xi | 1 | 2 | 3 | 4 | 5 |
| Hi | 2 | 9 | 11 | 16 | 12 |
Wobei 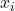 der Note entspricht und
der Note entspricht und 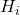 die absolute Häufigkeit der Beobachtung wiedergibt.
die absolute Häufigkeit der Beobachtung wiedergibt.
Der Notenspiegel lässt sich nun wie folgt bestimmen:
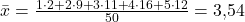
Folglich beträgt das arithmetische Mittel für die Klausuren der 50 Studierenden also 3,54.
Beispiel (relative Häufigkeit)
Die Studierenden eines Studiengangs schreiben eine Statistikklausur. Aus Datenschutzgründen werden die Ergebnisse nur in anonymisierter Form als Notenverteilungen veröffentlicht. Uns liegt folgende Häufigkeitstabelle vor.
| xi | 1 | 2 | 3 | 4 | 5 |
| hi | 0,1 | 0,3 | 0,2 | 0,25 | 0,15 |
Wobei 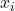 wieder der Note entspricht und
wieder der Note entspricht und 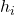 die relative Häufigkeit der Beobachtung wiedergibt.
die relative Häufigkeit der Beobachtung wiedergibt.
Die Studierenden möchten nun bestimmen wie gut oder schlecht die Klausur in diesem Jahr ausgefallen ist. Dazu benutzen sie die Formel zum gewichteten arithmetischen Mittel bei relativen Häufigkeiten:
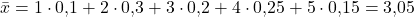
Damit weißt du, dass der Notendurchschnitt für die Klausuren der Studierenden also 3,05 beträgt.
Fehlende Messwerte bestimmen
Es kann vorkommen, dass bereits der Mittelwert bestimmt ist, jedoch die Daten zu einzelnen Beobachtungen fehlen. In solch einem Fall kannst du die fehlenden Messwerte durch eine kleine Umformung der Formel ermitteln.
Stell dir etwa vor, dass du 5 Messwerte hast, von denen einer unbekannt ist. Allerdings kennst du bereits das arithmetische Mittel aller Messwerte, nämlich 3.
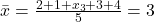
Um den fehlenden Messwert zu ermitteln multiplizierst du beide Seiten der Gleichung mit der Anzahl der Messwerte, also mit 5. Damit erhältst du:
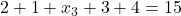
Diese Gleichung musst du jetzt nur noch nach 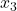 umstellen und ausrechnen:
umstellen und ausrechnen:
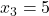
Wie du siehst ist die Note des dritten Studierenden also 5.
Das arithmetische Mittel ist der Durchschnitt von statistischen Daten. Du nennst es deshalb auch Durchschnittswert oder Mittelwert. Um ihn zu berechnen, addierst du alle Daten und teilst das Ergebnis durch die Anzahl der Daten.


