absolute und relative Häufigkeit
Du willst alles über die absolute und relative Häufigkeit wissen? Dann bist du hier genau richtig! Wenn du dich beim Lernen lieber zurücklehnen willst, dann schau dir doch einfach unser Video
zu dem Thema absolute und relative Häufigkeit an.
Inhaltsübersicht
Absolute und relative Häufigkeit einfach erklärt
Die absolute Häufigkeit ist identisch zum Begriff Anzahl. Ein Beispiel: Du spielst Basketball und triffst von 10 Würfen genau 2 Stück. Die absolute Häufigkeit einen Treffer zu landen ist damit 2.
Die relative Häufigkeit kannst du bestimmen, indem du die absolute Häufigkeit durch die Anzahl aller Versuche teilst. Diese kannst du hier also wie folgt berechnen: 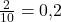 . Die relative Häufigkeit, dass du einen Treffer landest, liegt also bei 20%.
. Die relative Häufigkeit, dass du einen Treffer landest, liegt also bei 20%.
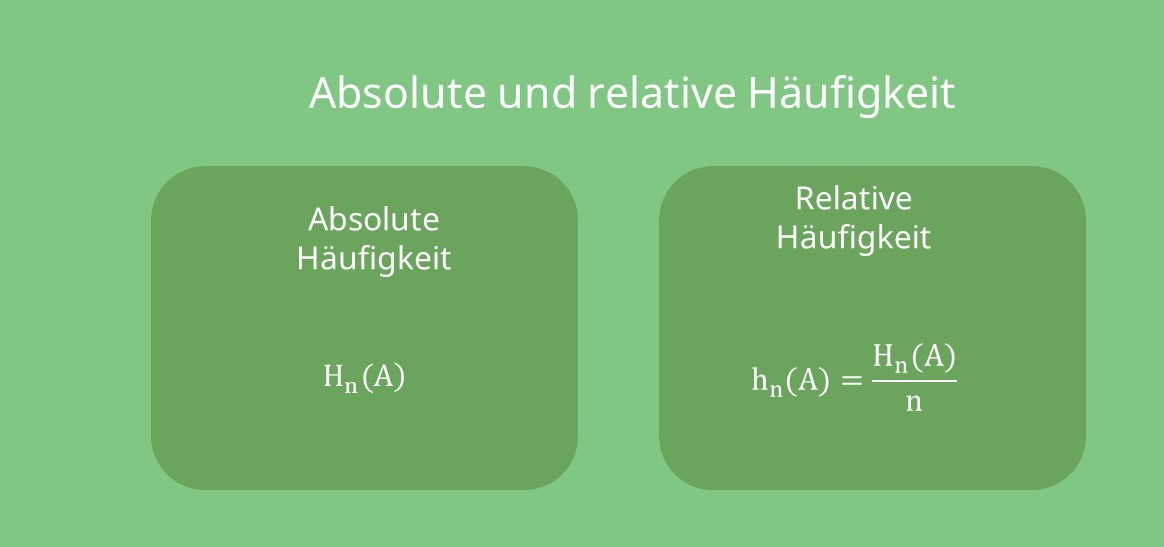
Mit der absoluten Häufigkeit gibst du an, wie oft ein bestimmtes Ereignis eintritt. Mit der relativen Häufigkeit beschreibst du dagegen den Anteil der absoluten Häufigkeit an der Gesamtzahl der Versuche. Deshalb kannst du sie berechnen, indem du die absolute Häufigkeit durch die Versuchsanzahl teilst.
Diese Definitionen kannst du auch in ihren Formeln erkennen:
A steht dabei für das zu untersuchende Ereignis, und n bezeichnet die Versuchsanzahl.
Absolute Häufigkeit Definition
Die absolute Häufigkeit misst die Häufigkeit des Auftretens eines bestimmten Elementarereignisses in einer Grundgesamtheit. Daher kann die absolute Häufigkeit auch umgangssprachlich als Ergebnis einer Zählung interpretiert werden. Die absolute Häufigkeit kann per Definition nur Ausprägungen annehmen, die im Bereich der natürlichen Zahlen sind (einschließlich der 0). Dies liegt augenscheinlich in der Natur einer Zählung. Generell unterscheidet man innerhalb der deskriptiven Statistik zwischen der absoluten Häufigkeit und der relativen Häufigkeit.
Absolute Häufigkeit berechnen
Nun stellt sich die Frage: Wie berechnet man die absolute Häufigkeit? Am besten versteht man die absolute Häufigkeit anhand eines Beispiels.
Absolute Häufigkeit Beispiel:
Ein klassisches Beispiel, um absolute Häufigkeit zu erklären ist das mehrmalige Werfen eines Würfels. Wenn der Würfel beispielsweise 100-mal geworfen wird und 22-mal das Ergebnis 6 herauskommt, folgt daraus, dass die absolute Wahrscheinlichkeit für das Merkmal 6 die 22 ist.
Absolute Häufigkeit Formel
Um die absolute Häufigkeit zu bestimmen, kann folgende Formel verwendet werden. Bei einem Versuch mit n Versuchen ist die Anzahl H (oft wird die absolute Häufigkeit mit H beschrieben) mit der ein Merkmal A in einer Stichprobe erscheint, als absolute Häufigkeit von Merkmal A definiert.
Häufige Schreibweise: 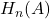
Relative Häufigkeit Definition
Die relative Häufigkeit ist definiert als der Anteil des Merkmals an der zugrundeliegenden Menge. Daher kann sie nur Werte zwischen 0 und 1 annehmen. Relative Häufigkeiten fungieren als wichtiger Baustein in der deskriptiven Statistik, um Verteilungen von Häufigkeiten unabhängig von n also der Größe der Stichprobe (Grundgesamtheit) darzustellen. Damit leistet sie einen wichtigen Beitrag zum Vergleich zweier verschieden großer Grundgesamtheiten.
Relative Häufigkeit berechnen
Am besten siehst du das direkt an einem Beispiel:
Beispiel:
Bei 100 Würfen mit einem Würfel ergibt sich wieder 22-mal das Ergebnis 6. Die absolute Häufigkeit beträgt also wieder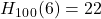 . Um jetzt die relative Häufigkeit zu erhalten wird die absolute Häufigkeit durch die Anzahl der Male, die der Würfel geworfen wurde, geteilt. In diesem Beispiel ergibt sich also:
. Um jetzt die relative Häufigkeit zu erhalten wird die absolute Häufigkeit durch die Anzahl der Male, die der Würfel geworfen wurde, geteilt. In diesem Beispiel ergibt sich also: 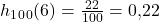 .
.
Relative Häufigkeit Formel
Die Relative Häufigkeit berechnet sich folglich mit folgender Formel:
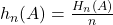
Du teilst also die absolute Häufigkeit H der Ausprägung A im Zufallsexperiment durch die der Stichprobe zugrundeliegende Menge n (Anzahl der Versuche).
Absolute und relative Häufigkeit: Häufigkeitstabelle
Eine beliebte Variante, um die absolute und relative Häufigkeit übersichtlich darzustellen ist eine Häufigkeitstabelle . In unserem Beispiel mit dem Würfel könnte eine diese so aussehen:
| Ausprägung des Würfels A | 1 | 2 | 3 | 4 | 5 | 6 |
| H100 | 12 | 15 | 14 | 18 | 19 | 22 |
| h100 | 0,12 | 0,15 | 0,14 | 0,18 | 0,19 | 0,22 |
| K100 | 0,12 | 0,27 | 0,41 | 0,59 | 0,78 | 1 |
Dabei steht H für die absolute Häufigkeitsverteilung, h für die relative Häufigkeitsverteilung und die Größe der Grundgesamtheit n beträgt 100. Die kumulierte Häufigkeit K kannst du durch das aufaddieren der relativen Wahrscheinlichkeiten berechnen und muss, sobald alle Merkmale verrechnet sind, immer 1 ergeben.
Wichtig ist das eine Häufigkeitstabelle nicht strikt normiert ist so können zum Beispiel je nach Bedarf die kumulierten Häufigkeiten, oft auch als Summenhäufigkeiten bezeichnet, weggelassen werden.
Variante Häufigkeitstabelle: Kontingenztabelle
Eine besondere Variante von Häufigkeitstabellen sind Kontingenztabellen (auch Kreuztabellen genannt). Die Besonderheit von Kontingenztabellen ist, dass man mit ihrer Hilfe in der Lage ist das gemeinsame Auftreten mehrerer Merkmale zu erfassen.
Variante Häufigkeitstabelle: Vierfeldertafel
Oft ist auch von der Vierfeldertafel als Spezialfall von Häufigkeitstabellen und Kontingenztabellen die Rede. Vielleicht kennst du diese Variante noch aus der Schule. Grundsätzlich gilt, die Vierfeldertafel ist eine auf 2×2 normierte Kontingenztabelle.
Verhältnis zur Wahrscheinlichkeit
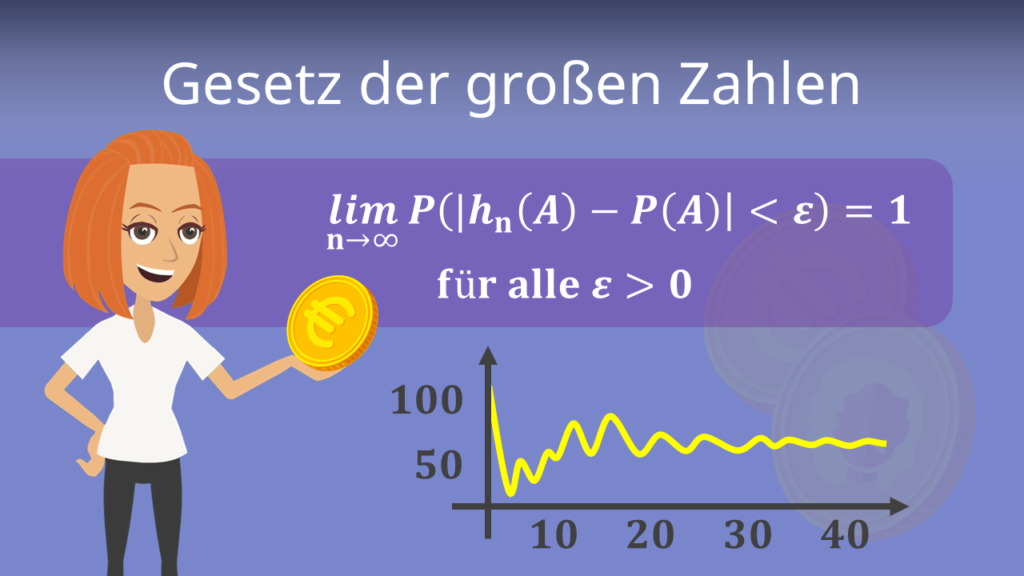
Laut dem Gesetz der großen Zahlen nähern sich relative Häufigkeit und die echte Wahrscheinlichkeit für ein Ereignis bei ausreichend vielen Versuchen immer weiter an, bis sie schlussendlich deckungsgleich sind.
Bei einem klassischem, sechsseitigem Würfel ist die Wahrscheinlichkeit für jede Zahl 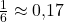 . Beim Vergleich mit der oben stehenden Häufigkeitstabelle mit 100 Versuchen wird ersichtlich das diese Wahrscheinlichkeiten bei keiner Ziffer erreicht wird. Bei der Durchführung von weiteren Versuchen werden sich die relativen Häufigkeiten immer weiter der Wahrscheinlichkeit
. Beim Vergleich mit der oben stehenden Häufigkeitstabelle mit 100 Versuchen wird ersichtlich das diese Wahrscheinlichkeiten bei keiner Ziffer erreicht wird. Bei der Durchführung von weiteren Versuchen werden sich die relativen Häufigkeiten immer weiter der Wahrscheinlichkeit 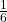 annähern.
annähern.
Mehr dazu erfährst du in unserem Video: