Baumdiagramm
Dieser Artikel liefert dir eine Antwort auf die Frage: Was ist ein Baumdiagramm? Wir zeigen, wie man ein Baumdiagramm erstellen und die Wahrscheinlichkeit berechnen kann.
Unser Video erklärt dir alles genau so verständlich wie der Artikel, aber in einem Bruchteil der Zeit die du zum Lesen brauchen würdest!
Inhaltsübersicht
Wahrscheinlichkeitsrechnung Baumdiagramm
Ein Baumdiagramm ist ein Hilfsmittel zur graphischen Darstellung von zueinander in Beziehung stehenden Ergebnissen innerhalb der Wahrscheinlichkeitsrechnung. Es ermöglicht mit Hilfe der Pfadregeln Zufallsexperimente übersichtlich abzubilden und die dazugehörigen Wahrscheinlichkeiten zu berechnen.
Baumdiagramm Erklärung
Mit Hilfe eines Baumdiagramms lassen sich folglich mehrstufige Zufallsexperimente übersichtlich darstellen. Die Wahrscheinlichkeiten für verschiedene Ergebnisse lassen sich so einfach berechnen. Durch Ergänzung der Zweigwahrscheinlichkeiten an den einzelnen Ästen werden diese zu sogenannten Wahrscheinlichkeitsbäumen. Die einzelnen Wahrscheinlichkeiten werden dabei für gewöhnlich als Dezimalbrüche angegeben. Anschließend kann man die Wahrscheinlichkeiten für verschiedene Ergebnisausgänge ganz einfach berechnen. Am besten kann man dies anhand eines Beispiels erklären.
Baumdiagramm Beispiele
Da das Baumdiagramm ein so einfaches und flexibles Hilfsmittel der Wahrscheilichkeitsrechnug in der Stochastik ist, lassen sich unzählige Anwendungsbeispiele finden. Klassische Beispiele sind das Werfen einer Münze oder eines Würfels. aber auch komplexere Zufallsexperimente wie Urnenmodelle oder das so genannte Ziegenproblem lassen sich durch ein Baumdiagramm graphisch abbilden. Durch das Ziegenproblem Baumdiagramm kann man beispielsweise rationale Entscheidungen bei Quizshows begründen. Der Kanditat muss eine von drei Türen auswählen, hinter welchen sich entweder Nieten ( eine Ziege) oder der Hauptgewinn (ein Auto ) befindet. Zusätzlich muss er sich nachdem eine Ziegentür geöffnet wurde entscheiden, ob er bei seiner ausgewählten Tür bleiben möchte oder nicht. Die dazugehörigen Wahrscheinlichkeiten können dabei im dem Baumdiagramm abgetragen werden und beantworten so die Frage, ob es für den Kandidaten vorteilhaft ist bei seiner Entscheidung zu bleiben.
Baumdiagramm erstellen
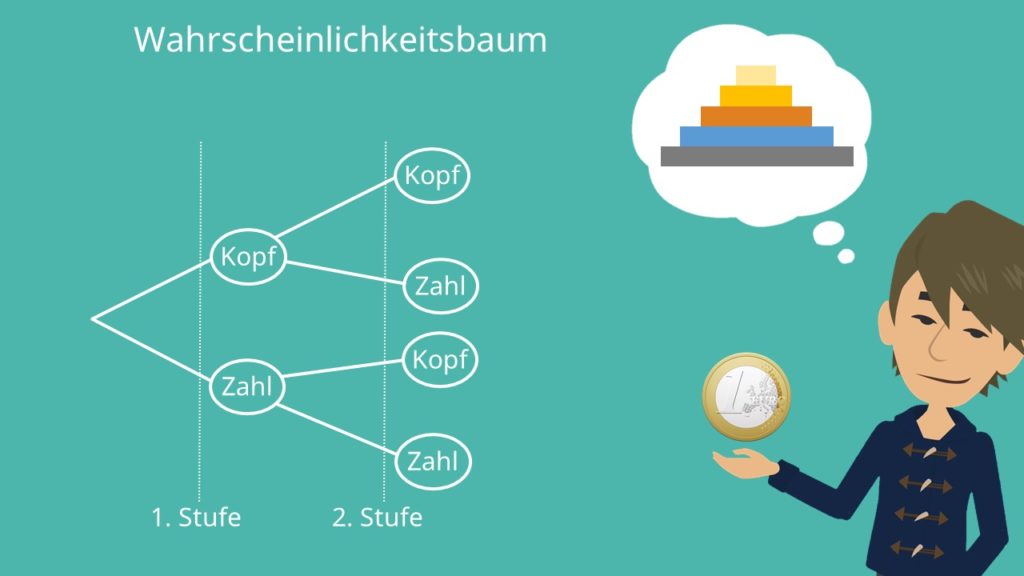
Um das ganze möglichst einfach zu halten, gehen wir im Folgenden zur Erstellung eines einfachen Baumdiagramms vom zweimaligen Werfen einer Münze aus. Um dieses Zufallsexperiment graphisch darzustellen, musst du dir überlegen wie viele „Stufen“ es hat. Da wir die Münze ja zweimal werfen, hat das Baumdiagramm in unserem Fall zwei Stufen. Dann musst du dir überlegen, was die Ereignisse sind, die eintreten können. In unserem Fall sind das Kopf und Zahl. Die Ereignisse werden in einem Baumdiagramm meist als Kreise dargestellt.
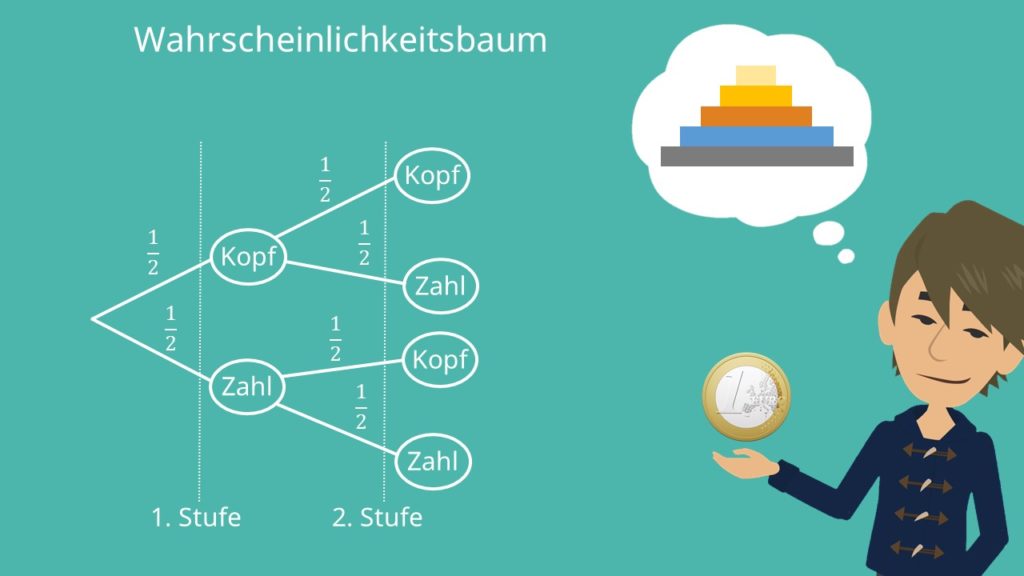
Die Linien, die die Ereignisse verbinden werden Pfade genannt, diese bestehen aus den einzelnen Zweigen des Wahrscheinlichkeitsbaums. An diese Pfade müssen wir im nächsten Schritt noch die jeweilige Zweigwahrscheinlichkeit abtragen. Bei unserem Beispiel ist das ganz einfach. Egal ob man die Münze einmal, zweimal oder auch fünfmal wirft, die Wahrscheinlichkeit für Kopf oder Zahl bleibt für jeden Wurf 50%. Wir können also jeden Zweig mit dem Wert 0,5 beschriften.Die Wahrscheinlichkeiten sind immer jeweils sind in diesem einfachen Beispiel also immer 0,5.
Mit dessen Hilfe können wir nun die Wahrscheinlichkeit für verschiedene Ergebnisse berechnen. Zum Beispiel, dass wir zweimal hintereinander Zahl werfen. Dazu musst du die erste Pfadregel, auch Produktregel genannt, anwenden.
Produktregel
Die Produktregel wird auch erste Pfadregel genannt. Sie besagt dass man, um die Wahrscheinlichkeit eines bestimmten Versuchsausgangs zu erhalten, die einzelnen Zweigwahrscheinlichkeiten multiplizieren muss.
Um die Wahrscheinlichkeit für das Ergebnis „Zweimal hintereinander Zahl“ zu berechnen, müssen wir also den entsprechenden Zweigen des Baumdiagramms folgen und diese multiplizieren. Wir rechnen also 0,5 mal 0,5 gleich 0,25. Die Pfadwahrscheinlichkeit beträgt also 25%.
Allgemein kann man sich merken, dass man die Produktregel anwenden muss, wenn der Versuchsausgang und die dazugehörigen Wahrscheinlichkeiten mit UND verknüpft sind. In unserem Fall soll also die Wahrscheinlichkeit berechnet werden Zahl UND dann nochmal Zahl zu erhalten.
Summenregel
Die Summenregel ist auch als Additionsregel oder zweite Pfadregel bekannt. Sie dient dazu, um die Wahrscheinlichkeit mehrerer Versuchsausgänge zu berechnen. Die Pfadwahrscheinlichkeiten der einzelnen Ergebnisse müssen laut dieser Regel addiert werden.
Als nächstes möchten wir berechnen, mit welcher Wahrscheinlichkeit einmal Kopf und einmal Zahl geworfen wird. Die Reihenfolge ist dabei egal. Dazu brauchen wir zusätzlich zur Produktregel auch die zweite Pfadregel.
Allgemein kann man sich merken, dass die Summenregel benötigt wird, wenn die Wahrscheinlichkeiten zusätzlich mit ODER verknüpft werden.
In unserem Fall müssen wir also die Wahrscheinlichkeit für die Ergebnisse „Erst Kopf dann Zahl“ ODER „Erst Zahl dann Kopf“ berechnen und diese dann addieren. Wir rechnen also:
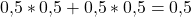
Die Zweigwahrscheinlichkeit einmal Zahl und einmal Kopf zu werfen beträgt also 50%.
Baumdiagramm Aufgaben
So, das waren auch schon die wichtigsten Grundlagen zum Baumdiagramm! Zum Abschluss schauen wir uns noch ein etwas komplizierteres Beispiel an. Mit dem Baumdiagramm lassen sich zum Beispiel auch Zufallsexperimente basierend auf dem Urnenmodell abbilden und deren Wahrscheinlichkeit berechnen. Stellen wir uns vor, in einer Urne befinden sich 2 blaue und 8 rote Kugeln. Nun ziehst du nacheinander dreimal jeweils eine Kugel aus der Urne, ohne diese wieder zurückzulegen.
Baumdiagramm ohne Zurücklegen
Dieses mehrstufige Zufallsexperiment wird auch „Ziehen ohne Zurücklegen“ genannt, und wird von uns in einem separaten Video zum Urnenmodell noch einmal genauer betrachtet. Hier zeigen wir dir aber, wie du Aufgaben zu diesem Experiment auch mit dem Baumdiagramm lösen kannst.
Baumdiagramm zeichnen
Grundsätzlich können wir das Baumdiagramm genau wie beim vorherigen Beispiel zeichnen. Jede Ziehung aus der Urne steht für eine Stufe. Die Ereignisse sind entweder eine blaue oder eine rote gezogene Kugel. Nur bei den Wahrscheinlichkeiten wird es diesmal etwas komplizierter. Beim ersten Zug ist es noch relativ eindeutig. Berechnen wir nun die Wahrscheinlichkeiten welche du neben den Zweigen des gezeichneten Baumdiagramms notieren musst.
Da 8 von 10 Kugeln rot sind, beträgt die Zweigwahrscheinlichkeit eine rote Kugel zu ziehen 80%, eine blaue entsprechend 20%. Beim zweiten Zug musst du allerdings aufpassen: da wir nach dem ersten Zug die Kugel nicht mehr zurücklegen, befinden sich nur noch 9 Kugeln in der Urne. DieWahrscheinlichkeit, eine rote Kugel zu ziehen, nachdem schon einmal eine rote Kugel gezogen wurde, beträgt jetzt also 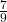 , da von den insgesamt 9 Kugeln noch 7 rot sind.
, da von den insgesamt 9 Kugeln noch 7 rot sind.
Nach dieser Logik kannst du nun alle Pfadwahrscheinlichkeiten bestimmen. Um dich zu kontrollieren, kannst du die Wahrscheinlichkeiten, die von einem Ereignis ausgehen, addieren – dabei muss immer 1 herauskommen.
Wahrscheinlichket berechnen
So, nun sollst du mit dem fertig erstellten Baumdiagramm die Wahrscheinlichkeit dafür berechnen, erst zwei blaue und dann eine rote Kugel zu ziehen. Dazu musst du einfach mit der Produktregel wieder die Pfade entsprechend entlang gehen und die Wahrscheinlichkeiten der Zweige multiplizieren. Da nur zwei blaue Kugeln in der Urne sind, beträgt die Wahrscheinlichkeit nach zweimal blau eine rote Kugel zu ziehen 100%. Wir rechnen also
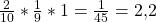
Die Wahrscheinlichkeit, erst zwei blaue und dann eine rote Kugel zu ziehen, beträgt also circa 2,2%. Analog kannst du auch die Pfadwahrscheinlichkeit für viele andere Ergebnisse bestimmen.
Baumdiagramm Pfadregeln
Das war auch schon alles Wichtige zum Baumdiagramm! Zur Wiederholung hier noch einmal die beiden Pfadregeln:
- Erste Pfadregel (Produktregel): Die Wahrscheinlichkeit eines einzelnen Ergebnisses ergibt sich aus dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu diesem Ergebnis führt.
- Zweite Pfadregel (Summenregel): Die Wahrscheinlichkeit eines Ereignisses, dass mehrere Ergebnisse umfasst, müssen die Wahrscheinlichkeiten der einzelnen Ergebnisse summiert werden.