Betriebsoptimum Betriebsminimum
In diesem Artikel erklären wir dir den Unterschied zwischen Betriebsoptimum und Betriebsminimum. Außerdem gehen wir auf die Themen Betriebsoptimum berechnen und Betriebsminimum berechnen ausführlich ein.
Du bist zu beschäftigt, um dir das alles selbst durchzulesen? Dann schau dir doch einfach unser Video zu Betriebsoptimum Betriebsminimum an.
Inhaltsübersicht
Betriebsoptimum Definition
Beginnen wir zuallererst mit der Definition des Begriffes Betriebsoptimum. Dieses liegt beim Minimum der durchschnittlichen Stückkosten. Das bedeutet, dass hier sowohl die variablen Stückkosten als auch die fixen Stückkosten mit in die Kalkulation einfließen. Am Betriebsoptimum macht das Unternehmen also weder Verlust noch Gewinn.
Wichtig! Es handelt sich um ein Synonym für die langfristige Preisuntergrenze und kann genauso berechnet werden. Kommen wir also zur Formel für das Betriebsoptimum.
Betriebsoptimum Formel
Um das Betriebsoptimum berechnen zu können, musst du zuerst wissen, ob es sich bei der gegebenen Kostenfunktion um eine lineare oder eine quadratische Funktion handelt.
- Zuerst betrachten wir den Fall einer linearen Kostenfunktion, also:
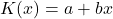
Hier sind  die fixen Kosten und
die fixen Kosten und 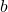 die linearen Kosten. Die Berechnung des Betriebsoptimums ist nun ganz einfach. Du teilst lediglich die Kostenfunktion durch die produzierte Menge, also:
die linearen Kosten. Die Berechnung des Betriebsoptimums ist nun ganz einfach. Du teilst lediglich die Kostenfunktion durch die produzierte Menge, also:
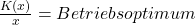
- Nun betrachtet wir den etwas komplizierteren Fall, nämlich wenn die Kostenfunktion einen höheren Grad als eins hat, also beispielsweise:
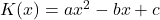
In diesem Fall sind  und
und 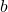 deine variablen Kosten und
deine variablen Kosten und  deine fixen Kosten. Um nun auf das Betriebsoptimum zu kommen, ermittelst du erst die Stückkostenfunktion. Diese leitest du dann nach
deine fixen Kosten. Um nun auf das Betriebsoptimum zu kommen, ermittelst du erst die Stückkostenfunktion. Diese leitest du dann nach  ab und setzt das Ganze gleich 0. In Formelschreibweise wäre das dann:
ab und setzt das Ganze gleich 0. In Formelschreibweise wäre das dann:
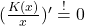
Nachdem du die Gleichung dann nach  aufgelöst hast, setzt du das dann in die Stückkostenfunktion ein und erhältst das Betriebsoptimum.
aufgelöst hast, setzt du das dann in die Stückkostenfunktion ein und erhältst das Betriebsoptimum.
Um dir die Frage „Was ist das Betriebsoptimum?“ noch besser erklären zu können, schauen wir uns nun zwei einfache Rechenbeispiele an.
Betriebsoptimum berechnen
Beginnen wir wieder mit dem einfacheren von den beiden Fällen, der lineare Kostenfunktion.
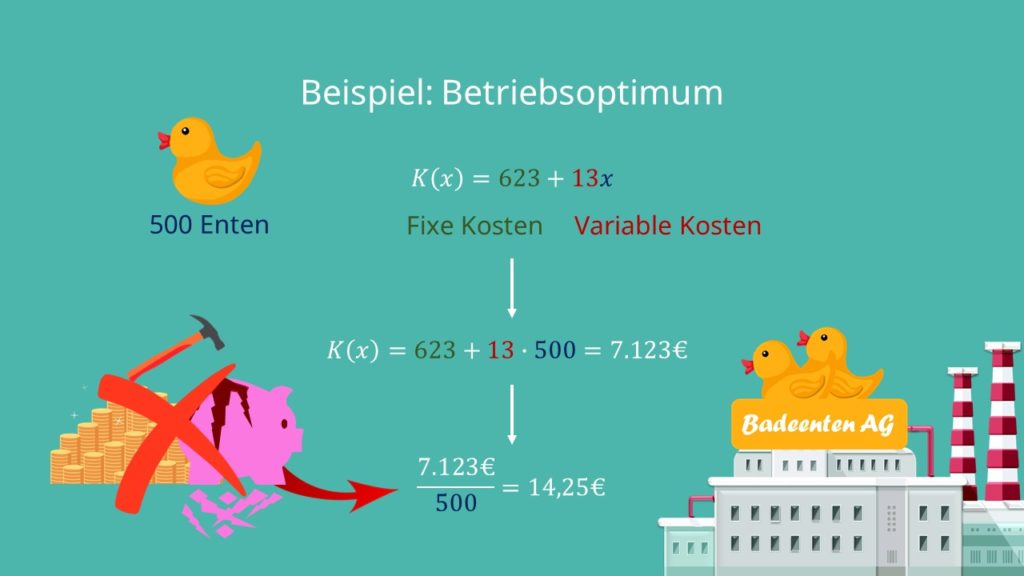
Stell dir vor, dein Unternehmen produziert Gummienten. Deine Kostenfunktion könnte beispielsweise
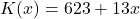
lauten.
Für die Produktion einer Gummiente fallen also variable Kosten in Höhe von 13€ und Fixkosten von 623€ an. Nehmen wir an, du produzierst 500 Gummienten. Dann setzt du diese Produktionsmenge  in die Kostenfunktion ein und teilst das Ganze durch 500. Das sieht dann so aus:
in die Kostenfunktion ein und teilst das Ganze durch 500. Das sieht dann so aus:
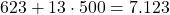
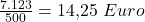
Du kommst also auf ein Betriebsoptimum von 14,25 €. Wenn du diesen Preis für deine Gummienten ansetzt, dann macht dein Unternehmen weder Gewinn noch Verlust.
Kommen wir nun zu einem etwas komplizierteren Beispiel, nämlich mit einer quadratischen Kostenfunktion. Der Einfachheit halber bleiben wir bei unserer Gummientenfabrik, allerdings lautet die neue Kostenfunktion nun:
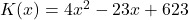
Wie wir oben bereits festgestellt haben, müssen wir diese Kostenfunktion zuerst wieder durch unsere produzierte Menge, nämlich  , teilen, um auf die durchschnittlichen Stückkosten (kurz TDK) zu kommen, also:
, teilen, um auf die durchschnittlichen Stückkosten (kurz TDK) zu kommen, also:
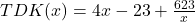
Diese leiten wir nun nach  ab und setzten sie gleich Null. Danach lösen wir das ganze nach
ab und setzten sie gleich Null. Danach lösen wir das ganze nach  auf.
auf.
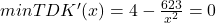
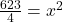
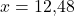
Die Menge für das Betriebsoptimum ist also 12,48. Als letzten Schritt müssen wir diese Menge noch in die Funktion der Durchschnittskosten einsetzen und erhalten:
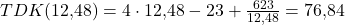
Diese 76,84€ sind nun unser Betriebsoptimum.
Der zweite Begriff der im Zusammenhang mit dem Betriebsoptimum steht ist das Betriebsminimum.
Betriebsminimum Definition
Das Betriebsminimum wird als das Minimum der variablen Stückkosten definiert. Hier werden also kurzfristig die Fixkosten vernachlässigt. Dies kann aus verschiedenen strategischen Gründen eine solide Taktik sein. Beispielsweise um Wettbewerber zu verdrängen, die mit einem solch niedrigen Preis nicht mithalten können. Allerdings muss einem bewusst sein, dass hier ein kalkulierter Verlust, nämlich in Höhe der Fixkosten entsteht.
Das Betriebsminimum ist ein Synonym für die kurzfristige Preisuntergrenze und wird genauso berechnet.
Betriebsminimum Formel
Du fragst dich sicher: Was ist das Betriebsminimum? Und wie kann ich es berechnen? Wir erklären es dir.
Die Formel zur Berechnung des Betriebsminimums ist eigentlich dieselbe wie die zur Berechnung des Betriebsoptimums, nur mit einem entscheidenden Unterschied. Die Grundlage ist nicht die gesamte Kostenfunktion, sondern nur die variablen Kosten. Diese erkennt man immer an dem Faktor  . Wenn du diese hast, dann berechnest du daraus die durchschnittlichen variablen Stückkosten.
. Wenn du diese hast, dann berechnest du daraus die durchschnittlichen variablen Stückkosten.
Wenn also die Kostenfunktion
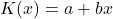
lautet, dann sind 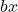 die variablen Kosten
die variablen Kosten 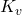 und das Betriebsminimum:
und das Betriebsminimum:
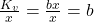
Also können wir festhalten: Bei einer einfachen linearen Kostenfunktion ist 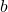 das Betriebsminimum. Allerdings gibt es auch hier wieder den etwas schwereren Fall, nämlich bei einer Kostenfunktion höheren Grades. Hier gehen wir wieder wie folgt vor. Zuerst nehmen wir die variablen Kosten
das Betriebsminimum. Allerdings gibt es auch hier wieder den etwas schwereren Fall, nämlich bei einer Kostenfunktion höheren Grades. Hier gehen wir wieder wie folgt vor. Zuerst nehmen wir die variablen Kosten 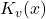 , teilen sie durch
, teilen sie durch  und leiten diesen Term nach
und leiten diesen Term nach  ab. Dann setzen wir ihn gleich 0. Das sieht dann folgendermaßen aus:
ab. Dann setzen wir ihn gleich 0. Das sieht dann folgendermaßen aus:
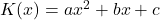
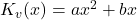
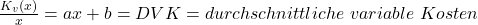
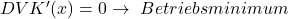
Um das ganze noch verständlicher zu gestalten, kommen hier noch zwei Rechenbeispiele.
Betriebsminimum berechnen
Wir steigen wieder zuerst mit der linearen Kostenfunktion ein. Stell dir vor, dein Unternehmen produziert Tischtennisbälle aus Plastik, dann wäre deine Kostenfunktion:
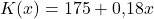
Für jeden produzierten Tischtennisball fallen also variable Kosten und fixe Kosten an. Um nun das Betriebsminimum zu berechnen, teilen wir einfach die variablen Kosten durch die Produktionsmenge  .
.
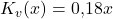
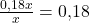
Somit kommen wir in diesem Fall auf ein Betriebsminimum von 0,18€. Das war doch ganz einfach, oder?
Zu guter Letzt schauen wir uns noch den Fall einer nicht linearen Kostenfunktion an, nämlich
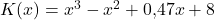
Als Erstes wollen wir wieder an die durchschnittlichen variablen Stückkosten herankommen. Dazu teilen wir die variablen Kosten durch  .
.
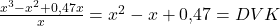
Anschließend leiten wir die durchschnittlichen variablen Stückkosten nach  ab und setzen sie gleich 0.
ab und setzen sie gleich 0.
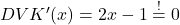
Wenn wir das nach x auflösen, kommen wir auf eine Menge von 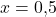 . Setzen wir diese in die Formel der variablen Durchschnittskosten ein, erhalten wir:
. Setzen wir diese in die Formel der variablen Durchschnittskosten ein, erhalten wir:
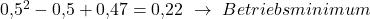
Im zweite Fall wäre das Betriebsminimum für unsere Tischtennisbälle also diesmal 0,22€.
Betriebsoptimum Betriebsminimum Zusammenfassung
Fassen wir noch einmal zusammen: Das Betriebsoptimum berechnet sich über die durchschnittlichen Stückkosten und gibt an, zu welchem Preis wir die Waren verkaufen müssten, um weder Gewinn noch Verlust zu machen. Es handelt sich hierbei um die langfristige Preisuntergrenze.
Das Betriebsminimum wiederum lässt sich über die durchschnittlichen variablen Stückkosten berechnen und vernachlässigt kurzfristig die fixen Kosten.