Boxplot
In diesem Artikel dreht sich alles um den Boxplot. Nach einer einfachen Erklärung zeigen wir, wie man diese Kastengrafik erstellt und wie man zu einem exemplarischen Datensatz einen Boxplot zeichnen kann mit Ausreißern und den dazugehörigen Whiskern.
Du fragst dich; Was ist ein Boxplot? Unser Video zeigt dir schnell und verständlich wie du einen Boxplot erstellen und so deine Daten in eine graphische Übersicht bringen kannst!
Inhaltsübersicht
Boxplot Erklärung
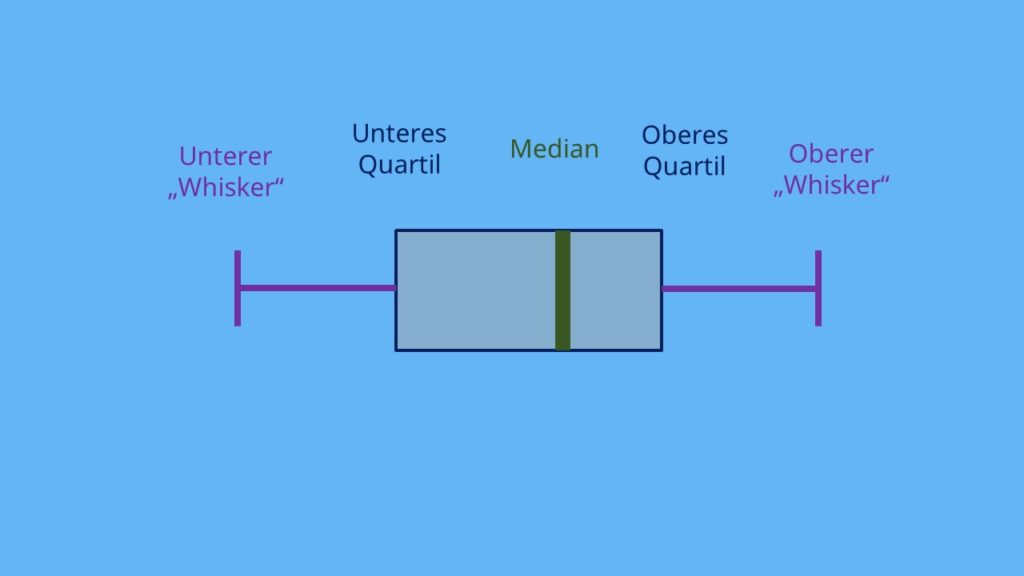
Der Boxplot, auch Box-Whisker-Plot oder im Deutschen Kastengrafik genannt, ist ein Diagramm, welches die übersichtliche Darstellung der wichtigsten robusten Lage- und Streuungsmaße ermöglicht. Es werden das Minimum, das untere Quartil, der Median, das obere Quartil und das Maximum abgebildet.
Boxplot Statistik
Um alles zu verstehen, solltest du diese unterschiedlichen Maße der Statistik bereits ausreichend beherrschen. Das Minimum, das untere Quartil, der Median, das obere Quartil und das Maximum gelten nicht umsonst als die wichtigsten 5 Quantile des Datensatzes.
Boxplot Interpretation
Die Darstellung deiner Daten in einem Box-Whisker-Plot liefert dir keine zusätzlichen Informationen. Boxplots bilden deine Daten lediglich strukturiert und übersichtlich ab. Daher beschränkt sich die Interpretation auf die Aussagen, welche man im Allgemeinen über das Minimum, das untere Quartil, den Median, das obere Quartil und das Maximum treffen kann. Dass Minimum und das Maximum den kleinsten beziehungsweise größten Wert deiner Daten angeben ist offensichtlich. Auch der Median lässt wenig Interpretationsspielraum. Er wird durch den Wert festgelegt, der sich genau in der Mitte deiner Daten befindet. Die Quartile verraten dir, wie viel Prozent der Werte kleiner beziehungsweise größer als ein bestimmter Wert sind. Wenn du dir nicht mehr ganz sicher bist, wie du Quartile interpretieren kannst, helfen dir unser Video zu den Quartilen oder auch das Video zum Thema Quantile bestimmt weiter! Aber wie genau sieht so eine Kastengrafik jetzt aus?
Boxplot erstellen
Er besteht aus der Box, die sich vom unteren bis zum oberen Quantil zieht und den beiden, sogenannten „Whisker“, zwei Linien, die das Rechteck mit dem Minimum beziehungsweise Maximum verbinden. Der Median wird als vertikaler Strich in der Box eingezeichnet.
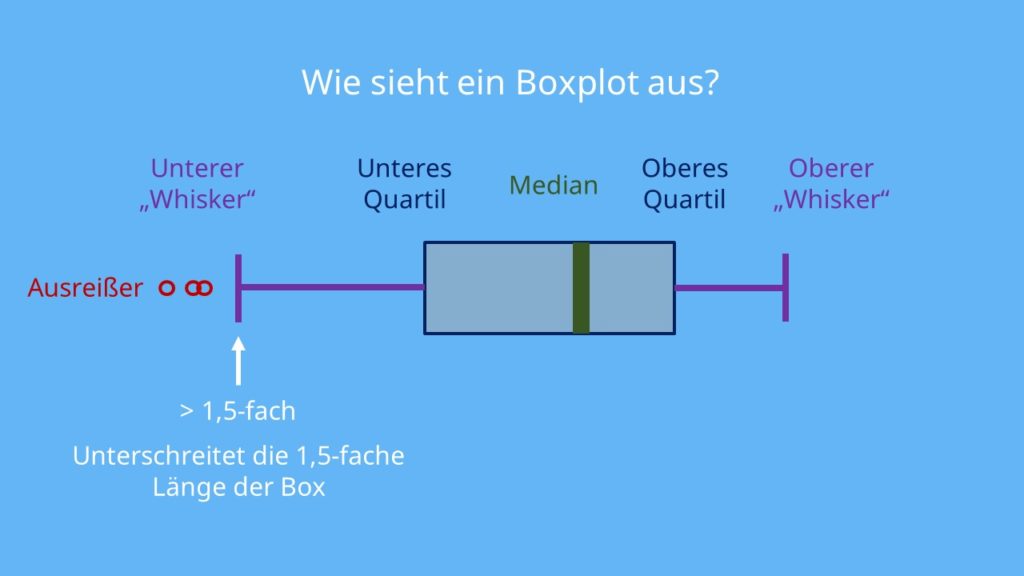
Es gibt eine Besonderheit. Sind die Whiskers länger als das 1,5-fache der Box, werden alle Werte, die darüber hinaus gehen als Ausreißer gekennzeichnet. Die Whiskers enden dann bei dem letzten Wert, der die 1,5-fache Länge der Box unterschreitet.
Da diese Ausnahme aber nicht fest definiert ist, ist sie nicht verpflichtend. Trotzdem geht man in den meisten Fällen so vor.
Boxplot zeichnen
Zum Abschluss wollen wir noch unseren eigene Kastengrafik für folgenden Datensatz zeichnen:
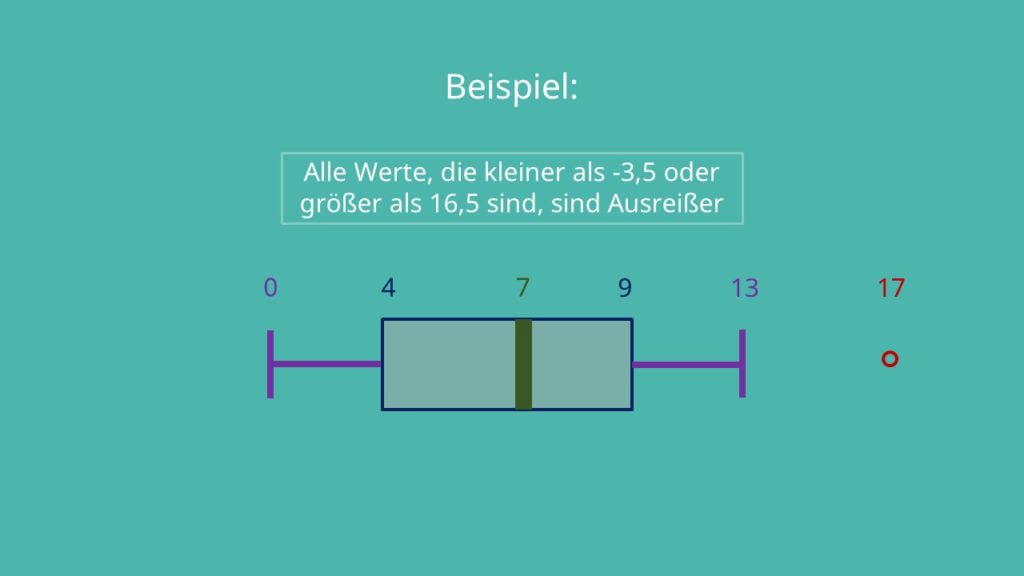
Bei diesen bereits sortierten Daten können Minimum, Median und Maximum direkt abgelesen werden. Auch die Ermittlung der 25 beziehungsweise 75 Prozent- Quantile sollten dir keine Probleme mehr bereiten:
Boxplot Ausreißer
Jetzt überprüfen wir noch, ob wir Ausreißer markieren müssen: Die eineinhalb fache Länge des Quartilsabstandes beträgt:
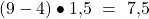
Das heißt alle Werte, die kleiner als – 3,5 oder größer als 16,5 sind, müssen als Ausreißer gekennzeichnet werden. Unser Maximum, die siebzehn, ist also der einzige Ausreißer.
Boxplot Whisker
Der linke Whisker entspricht dem vorher ermittelten Minimum und kann direkt eingezeichnet werden. Der rechte Whisker ist in unserem Beispiel nicht das Maximum der Daten, da es sich bei dem Wert 17 um einen Ausreißer handelt. Der rechte Whisker liegt somit beim nächstkleineren Wert, der 13.