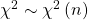Chi Quadrat Verteilung
Dieser Artikel behandelt die Chi Quadrat Verteilung und erklärt diese Wahrscheinlichkeitsverteilung anhand von einem einfachen Beispiel. Es wird gezeigt wie man die die Werte aus der Chi Quadrat Verteilung Tabelle ablesen kann und welche Rolle die Freiheitsgrade in diesem Zusammenhang spielen.
Ha-CHI! Das Lesen langer Texte löst bei dir allergische Reaktionen aus? In unserem Video wird dir die Chi Quadrat Verteilung einfach erklärt!
Inhaltsübersicht
Chi Quadrat Verteilung einfach erklärt
Die Chi Quadrat Verteilung ist eine stetige Wahrscheinlichkeitsverteilung, die für alle positiven, reellen Zahlen definiert ist. Sie findet in der Realität selten Anwendung und wird hauptsächlich für die Schätzung von Verteilungsparametern, wie zum Beispiel der Varianz , und bei Hypothesentests angewendet.
Chi Quadrat Verteilung Herleitung
Die genaue Formel der Verteilung ist ziemlich kompliziert und geht über die Anforderungen der meisten Statistikveranstaltungen hinaus. Zur Berechnung verwendest du ganz einfach wieder eine Verteilungstabelle.
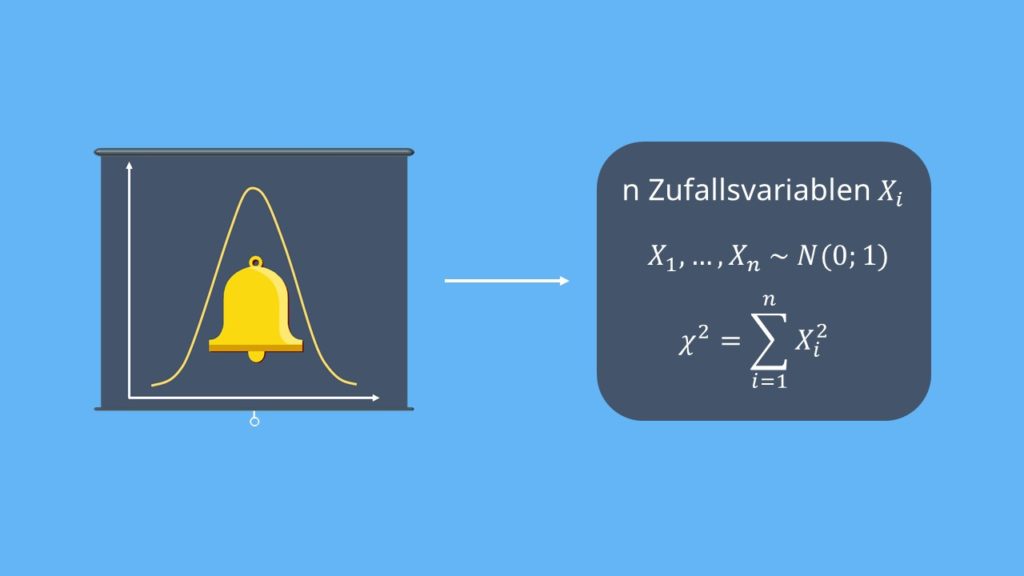
Die Chi Quadrat Verteilung kann aus der Normalverteilung abgeleitet werden. Haben wir also n Zufallsvariablen 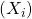 , die unabhängig und standardnormalverteilt sind,
, die unabhängig und standardnormalverteilt sind, 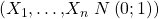 dann ergibt sich eine Verteilung mit n Freiheitsgraden aus der Summe der quadrierten Zufallsvariablen.
dann ergibt sich eine Verteilung mit n Freiheitsgraden aus der Summe der quadrierten Zufallsvariablen.
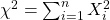
Chi Quadrat Freiheitsgrade
Freiheitsgrade sind die Werte, die frei verändert werden können, ohne dass dein betrachteter Parameter verändert wird. Die Anzahl der Freiheitgrade steigt allgemein mit zunehmender Stichprobengröße und sinkt mit der Anzahl der geschätzten Parameter.
Deutlicher wird das Ganze, wenn wir uns ein allgemeines Beispiel dazu überlegen: Sehen wir uns dazu drei beliebige Noten – z.B. 1,7 ; 1,3 und 3,0 – eines Studenten an und berechnen deren Mittelwert.
Wir erhalten ein arithmetisches Mittel von 2,0.
Wählen wir nun erneut zwei Noten aus, beispielsweise 2,7 und 2,3. In diesem Fall müsste unsere dritte Note eine 1,0 sein, damit wir erneut auf einen Notendurchschnitt von 2,0 kommen. Wir konnten hier folglich zwei Werte frei wählen, während der dritte Wert 1,0 annehmen musste. Allgemein kann man also sagen, dass die Anzahl der Freiheitsgrade n – 1 beträgt, wenn n die Anzahl unserer Messwerte ist.
Chi Quadrat Verteilung ablesen
Eine Chi-Quadrat-Verteilung mit zehn Freiheitsgraden und einem 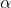 von 0,9 können wir also ganz einfach in der Tabelle ablesen:
von 0,9 können wir also ganz einfach in der Tabelle ablesen:
| df / Quantil (1-a) | 0,7 | 0,75 | 0,8 | 0,85 | 0,9 | 0,95 | 0,975 | 0,99 | 0,995 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.07 | 1.32 | 1.64 | 2.07 | 2.71 | 3.84 | 5.02 | 6.63 | 7.88 |
| 2 | 2.41 | 2.77 | 3.22 | 3.79 | 4.61 | 5.99 | 7.38 | 9.21 | 10.6 |
| 3 | 3.66 | 4.11 | 4.64 | 5.32 | 6.25 | 7.81 | 9.35 | 11.34 | 12.84 |
| 4 | 4.88 | 5.39 | 5.99 | 6.74 | 7.78 | 9.49 | 11.14 | 13.28 | 14.86 |
| 5 | 6.06 | 6.63 | 7.29 | 8.12 | 9.24 | 11.07 | 12.83 | 15.09 | 16.75 |
| 6 | 7.23 | 7.84 | 8.56 | 9.45 | 10.64 | 12.59 | 14.45 | 16.81 | 18.55 |
| 7 | 8.38 | 9.04 | 9.8 | 10.75 | 12.02 | 14.07 | 16.01 | 18.48 | 20.28 |
| 8 | 9.52 | 10.22 | 11.03 | 12.03 | 13.36 | 15.51 | 17.53 | 20.09 | 21.95 |
| 9 | 10.66 | 11.39 | 12.24 | 13.29 | 14.68 | 16.92 | 19.02 | 21.67 | 23.59 |
| 10 | 11.78 | 12.55 | 13.44 | 14.53 | 15.99 | 18.31 | 20.48 | 23.21 | 25.19 |
| 11 | 12.9 | 13.7 | 14.63 | 15.77 | 17.28 | 19.68 | 21.92 | 24.73 | 26.76 |
| 12 | 14.01 | 14.85 | 15.81 | 16.99 | 18.55 | 21.03 | 23.34 | 26.22 | 28.3 |
| 13 | 15.12 | 15.98 | 16.98 | 18.2 | 19.81 | 22.36 | 24.74 | 27.69 | 29.82 |
| 14 | 16.22 | 17.12 | 18.15 | 19.41 | 21.06 | 23.68 | 26.12 | 29.14 | 31.32 |
| 15 | 17.32 | 18.25 | 19.31 | 20.6 | 22.31 | 25 | 27.49 | 30.58 | 32.8 |
| 16 | 18.42 | 19.37 | 20.47 | 21.79 | 23.54 | 26.3 | 28.85 | 32 | 34.27 |
| 17 | 19.51 | 20.49 | 21.61 | 22.98 | 24.77 | 27.59 | 30.19 | 33.41 | 35.72 |
| 18 | 20.6 | 21.6 | 22.76 | 24.16 | 25.99 | 28.87 | 31.53 | 34.81 | 37.16 |
| 19 | 21.69 | 22.72 | 23.9 | 25.33 | 27.2 | 30.14 | 32.85 | 36.19 | 38.58 |
| 20 | 22.77 | 23.83 | 25.04 | 26.5 | 28.41 | 31.41 | 34.17 | 37.57 | 40 |
| 21 | 23.86 | 24.93 | 26.17 | 27.66 | 29.62 | 32.67 | 35.48 | 38.93 | 41.4 |
| 22 | 24.94 | 26.04 | 27.3 | 28.82 | 30.81 | 33.92 | 36.78 | 40.29 | 42.8 |
| 23 | 26.02 | 27.14 | 28.43 | 29.98 | 32.01 | 35.17 | 38.08 | 41.64 | 44.18 |
| 24 | 27.1 | 28.24 | 29.55 | 31.13 | 33.2 | 36.42 | 39.36 | 42.98 | 45.56 |
| 25 | 28.17 | 29.34 | 30.68 | 32.28 | 34.38 | 37.65 | 40.65 | 44.31 | 46.93 |
| 30 | 33.53 | 34.8 | 36.25 | 37.99 | 40.26 | 43.77 | 46.98 | 50.89 | 53.67 |
| 40 | 44.16 | 45.62 | 47.27 | 49.24 | 51.81 | 55.76 | 59.34 | 63.69 | 66.77 |
| 50 | 54.72 | 56.33 | 58.16 | 60.35 | 63.17 | 67.5 | 71.42 | 76.15 | 79.49 |
| 60 | 65.23 | 66.98 | 68.97 | 71.34 | 74.4 | 79.08 | 83.3 | 88.38 | 91.95 |
| 70 | 75.69 | 77.58 | 79.71 | 82.26 | 85.53 | 90.53 | 95.02 | 100.43 | 104.21 |
| 80 | 86.12 | 88.13 | 90.41 | 93.11 | 96.58 | 101.88 | 106.63 | 112.33 | 116.32 |
| 90 | 96.52 | 98.65 | 101.05 | 103.9 | 107.57 | 113.15 | 118.14 | 124.12 | 128.3 |
| 100 | 106.91 | 109.14 | 111.67 | 114.66 | 118.5 | 124.34 | 129.56 | 135.81 | 140.17 |
| 150 | 158.58 | 161.29 | 164.35 | 167.96 | 172.58 | 179.58 | 185.8 | 193.21 | 198.36 |
| 200 | 209.99 | 213.1 | 216.61 | 220.74 | 226.02 | 233.99 | 241.06 | 249.45 | 255.26 |
| 500 | 516.09 | 520.95 | 526.4 | 532.8 | 540.93 | 553.13 | 563.85 | 576.49 | 585.21 |
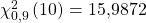
Wir erhalten einen Wert von 15,987.
Ab einem n größer 30 kannst du die Chi Quadrat Verteilung mittels der Standardnormalverteilung durch folgende Formel approximieren:
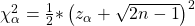
Wobei 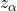 das entsprechende
das entsprechende 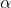 -Quantil der Standardnormalverteilung ist.
-Quantil der Standardnormalverteilung ist.
Chi Quadrat Verteilung Beispiel
Zum besseren Verständnis verdeutlichen wir das Ganze an dieser Stelle nochmal mit einem Beispiel. Haben wir also 50 Freiheitsgrade und erneut das 0,9 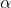 -Quantil, dann können wir die Chi-Quadrat-Verteilung approximieren.
-Quantil, dann können wir die Chi-Quadrat-Verteilung approximieren.
Zuerst suchen wir uns den Wert des 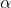 -Quantils in der Verteilungstabelle der Standardnormalverteilung. Er beträgt 1,28.
-Quantils in der Verteilungstabelle der Standardnormalverteilung. Er beträgt 1,28.
Jetzt setzen wir dieses Zwischenergebnis und unser n in die Formel ein und erhalten:
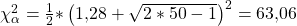
Easy! Wir haben ein approximatives Ergebnis von 63,06.
Damit sollten wir nun alle Fragen geklärt haben! Viel Spaß beim nächsten Thema!