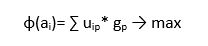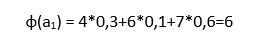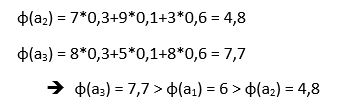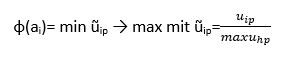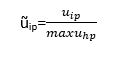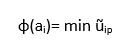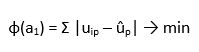Entscheidung bei Sicherheit
Du möchtest mit deinen Freunden euren nächsten gemeinsamen Urlaub planen, aber ihr könnt euch einfach für kein Reiseziel entscheiden? Nach diesem Beitrag wisst ihr endlich wohin es gehen soll!
Inhaltsübersicht
Zustand der Sicherheit
Man unterscheidet verschiedene Arten von Zuständen: Sicherheit, Risiko und Ungewissheit. In diesem Beitrag bewegen wir uns im Bereich der Sicherheit. Das heißt der tatsächliche Zustand der jeweiligen Alternative ist uns bekannt.
Urlaubsalternativen und Kriterien
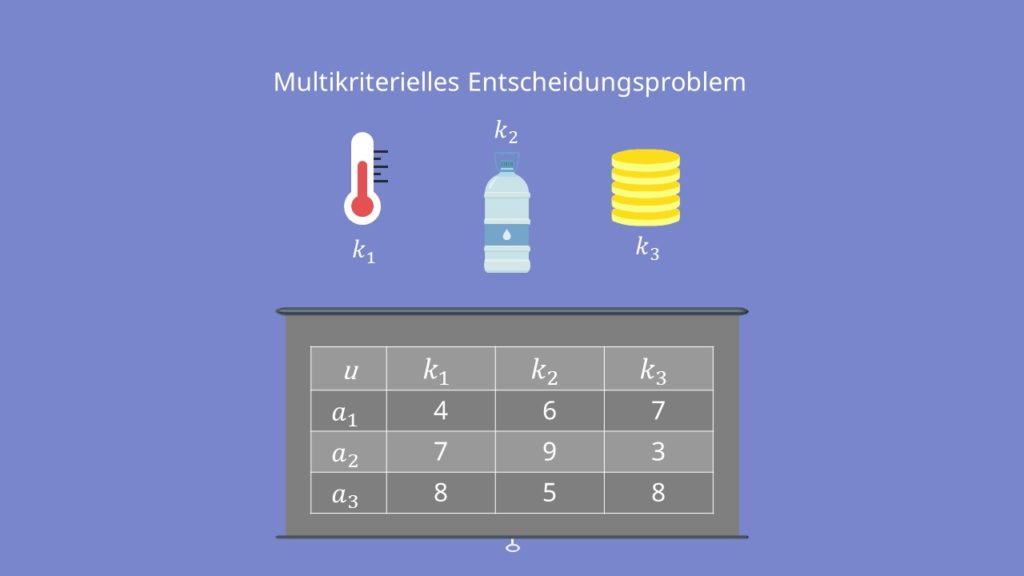
Kommen wir jetzt zurück zu unserem Beispiel, eurer Urlaubsplanung. Ihr habt euch im Vorfeld auf folgende Alternativen geeinigt: Es kommen entweder der Gardasee, die französische Côte d’Azur oder die türkische Riviera in Frage.
a1 = Gardasee
a2 = Côte d’Azur
a3 = türkische Riviera
Dabei legt ihr vor allem Wert auf die örtliche Temperatur, die Wasserqualität und das Preis-/Leistungsverhältnis. Das sind unsere verschiedenen Kriterien, nach denen wir die Reiseziele bewerten. Diese notieren wir mit einem kleinen k:
k1 = örtliche Temperatur
k2 = Wasserqualität
k3 = Preis-/Leistungsverhältnis
Multikriterelles Entscheidungsproblem
Du musst jetzt also nur noch den Urlaubsort bestimmen, der diese Ziele am besten erfüllt. Man spricht hier auch von einem multikriteriellen Entscheidungsproblem, da nicht nur ein, sondern mehrere Kriterien erfüllt sein müssen.
Wenn wir die Orte für jedes Kriterium auf einer Skala von 1-10 bewerten, wobei 10 der beste Wert ist, erhalten wir folgende Nutzenmatrix:
Vier spezielle Entscheidungsregeln
Als erstes wenden wir jetzt wieder das Dominanzprinzip an. In diesem Beispiel ist der Ausschluss eines Ortes allerdings nicht möglich, da keine der Alternativen dominiert wird.
Um eine Entscheidung zu treffen, müssen wir also weitere, speziellere Entscheidungsregeln heranziehen. Bei Sicherheit unterscheidet man dabei vier verschiedene: Zielgewichtung, Lexikographische Ordnung, Körth-Regel und Goal-Programming.
Entscheidung nach Zielgewichtung
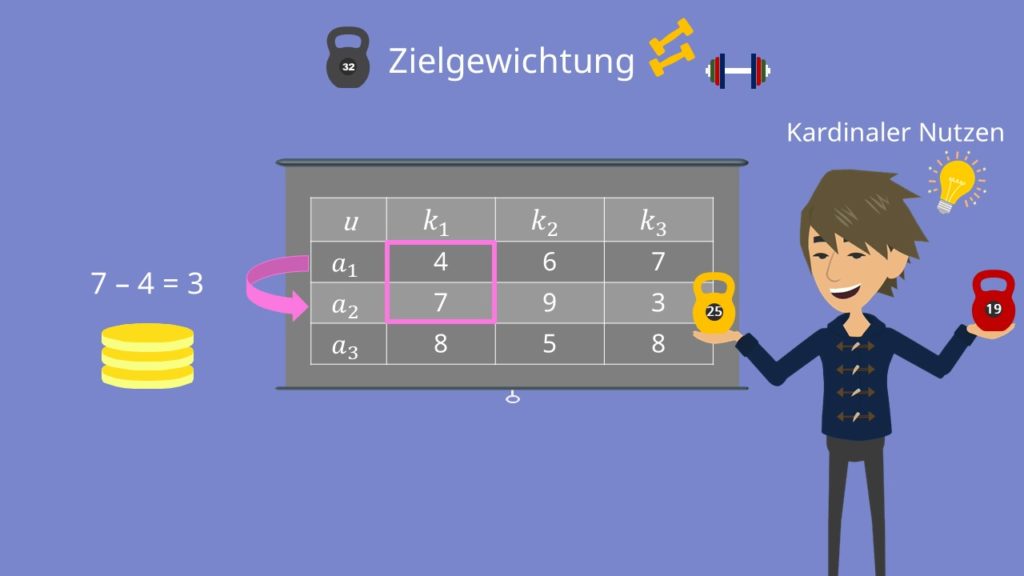
Schauen wir uns als erstes die Zielgewichtung näher an. Wie der Name schon sagt, gewichtet man bei dieser Regel einfach einige Ziele höher als andere. Dazu muss man allerdings einen kardinalen Nutzen voraussetzen. Das bedeutet, dass die Differenzen zwischen zwei Werten interpretierbar sein müssen.
Wenn du beispielsweise bei Kriterium 1 die Punktzahl von Alternative 1 von der Punktzahl von Alternative 2 abziehst, erhältst du 7 minus 4 gleich 3. Das ist interpretierbar, da man sagen kann: Alternative 2 ist um 3 Punkte besser als Alternative 1. Das muss aber nicht immer der Fall sein. Würden wir beispielsweise Noten betrachten, könnte man ja nicht sagen die Note 1 ist um „3“ besser als Note 4, denn es könnte ja eine 1- und eine 4+ sein. Noten wären daher ein Beispiel für ordinalen Nutzen.
Da bei uns aber ein kardinaler Nutzen vorliegt, können wir eine Zielgewichtung durchführen. Nach Rücksprache mit deinen Freunden entscheidet ihr euch, eure Kriterien so zu bewerten:
g1=0,3
g2=0,1
g3=0,6
Die örtliche Temperatur findet ihr relativ wichtig und gewichtet sie daher mit einem Faktor von 0,3. Die Wasserqualität ist euch nicht so wichtig, sie gewichtet ihr daher nur mit 0,1. Mit einem Faktor von 0,6 ist euch das Preis-/Leistungsverhältnis am wichtigsten.
Bei den Gewichtungen musst du vor allem darauf achten, dass sie in der Summe genau 1 ergeben. Nachdem wir diese festgelegt haben, können wir nun unsere Bewertungsfunktion Phi von a anwenden:
Diese Formel drückt aus, dass du die Summe der einzelnen Nutzenwerte einer Alternative mit den jeweiligen Gewichtungen multiplizieren musst und dann diejenige Alternative wählst, die den höchsten Wert für Phi erreicht.
In unserem Beispiel sieht das dann so aus:
Für die anderen 2 Alternativen ergibt sich ɸ analog.
Da Alternative 3 den höchsten Wert Phi erreicht, entscheidet ihr euch gemäß der Zielgewichtung also für die türkische Riviera.
Entscheidung nach lexikographischer Ordnung
Einer deiner Freunde ist mit diesem Ergebnis jedoch nicht zufrieden und schlägt daher vor, die lexikografische Ordnung anzuwenden. Hier ordnet man einfach die Ziele nach Wichtigkeit. Das wichtigste Ziel entscheidet dann über die Reihung der Aktionen. Nur wenn man beim wichtigsten Ziel indifferent zwischen zwei Aktionen ist, wird das zweitwichtigste Ziel betrachtet und so weiter.
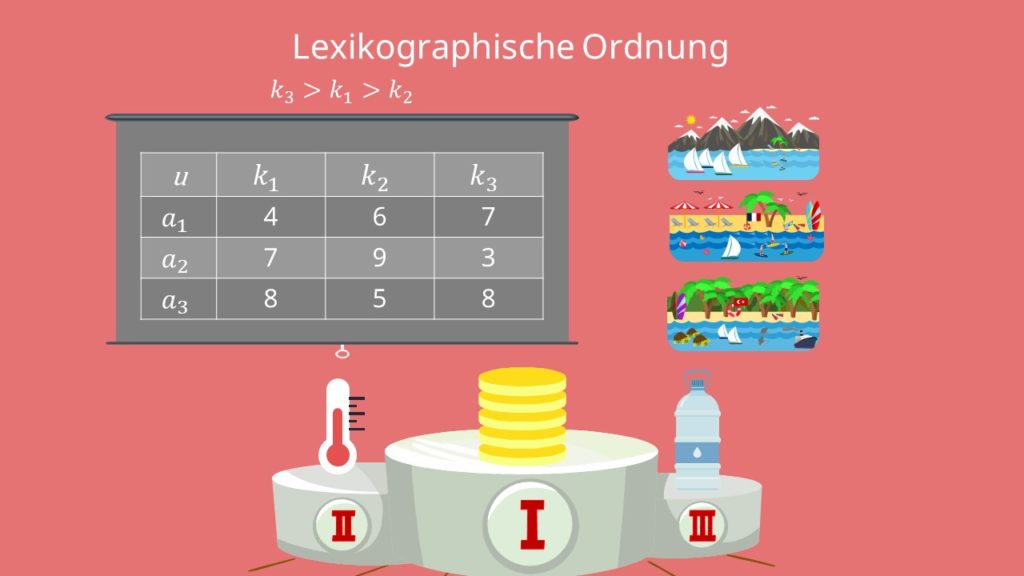
Wie wir festgestellt haben, gilt bei euch folgende Reihung der Ziele:
k3>k1>k2
Schauen wir uns also die Ausprägungen der Alternativen beim Kriterium Preis-/Leistung an.
Bei diesem Kriterium hat wieder die Alternative 3 mit 8 Punkten die Nase vorn. Ihr würdet euch also auch hier für die türkische Riviera entscheiden.
Entscheidung nach der Körth-Regel
Da dein Freund aber immer noch nicht überzeugt ist, möchte er noch die Körth-Regel anwenden. Auch hier muss vorher wieder auf kardinalen Nutzen geprüft werden. Bei der Körth-Regel wählt man die Aktion mit dem besten Worst-Case-Szenario. Die Bewertungsfunktion sieht dann so aus:
Sieht ganz schön kompliziert aus, aber an unserem Beispiel wirst du gleich sehen, dass diese Regel gar nicht so schwer ist!
Der erste Teil der Bewertungsfunktion drückt aus, dass wir den Wert ũ minimieren müssen. Dazu müssen wir unsere Nutzenmatrix u aber erst in u Welle transformieren. Dazu steht im hinteren Teil der Bewertungsfunktion folgende Formel:
Als erstes müssen wir die Spaltenmaxima ermitteln, also zu jedem Kriterium die Alternative, die die höchste Punktzahl erreicht. Jetzt müssen wir nur noch die einzelnen Werte durch das jeweilige Spaltenmaximum teilen.
Um den neuen Wert des Kriteriums k1 für die Alternative a1 zu erhalten, müssen wir also den alten Wert durch das Spaltenmaximum teilen. Wir rechnen also 4 geteilt durch 8, ergibt 0,5. Alle anderen Werte ergeben sich analog.
Wenn du die Nutzenmatrix erfolgreich transformiert hast, können wir wieder auf den ersten Teil der Bewertungsfunktion zurückkommen.
Wir wählen also einfach den kleinsten Wert jeder Alternative und erhalten somit unsere Zeilenminima.
Von den Zeilenminima musst du jetzt nur noch den größten Wert auswählen. Dadurch erhältst du die Alternative, die von den schlechtest möglichen Werten noch den besten erreicht. In unserem Beispiel ist das mit einem Wert von 0,6 wieder Alternative 3, die türkische Riviera.
Entscheidung nach Goal-Programming
Dein Freund ist fast überzeugt, aber eine letzte Regel möchte er noch ausprobieren und zwar das sogenannte Goal-Programming. Auch bei dieser Regel wird ein kardinaler Nutzen vorausgesetzt. Hier werden für jedes Kriterium Planzahlen vorgegeben, die wir als û notieren. Je näher der Wert der Alternative an der jeweiligen Planzahl liegt, desto besser. In unserem Beispiel ist es sinnvoll, für alle drei Kriterien als Planzahl 10 zu wählen, da das ja die optimale Punktzahl ist.
Es ergeben sich also folgende Planzahlen:
û1=10 û2=10 û3=10
Die Bewertungsfunktion sieht folgendermaßen aus:
Jetzt müssen wir wieder unsere ursprüngliche Nutzenmatrix transformieren, indem wir den Betrag aus der Differenz zwischen den Planzahlen und den tatsächlichen Werten berechnen.
Der Wert der Alternative 1 bei Kriterium 1 ergibt sich also so: |4-10|=6.
Alle anderen Werte ergeben sich analog. Jetzt musst du nur noch die Summe über die Zeilen bilden und dann die Alternative wählen, die den kleinsten Summenwert und somit die geringste Abweichung von den Planzahlen aufweist. Auch bei dieser Regel geht wieder Alternative 3 mit einem Wert von 9 als Sieger hervor.
Geschafft! Jetzt konntest du deinen Freund von der türkischen Riviera überzeugen und ihr könnt euren Urlaub endlich buchen! Viel Spaß am Strand!