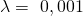Exponentialverteilung
Hier erfährst du alles zur Exponentialverteilung mitsamt Anwendungsbeispielen, Besonderheiten und den zugehörigen Formeln für die Dichte, die Verteilungsfunktion und den Erwartungswert.
Keine Lust zu lesen? Unser Video wird dein Wissen zur Exponentialverteilung exponentiell steigern, ohne dass du diesem langen Artikel Beachtung schenken musst!
Inhaltsübersicht
Exponentialverteilung Statistik
Die Exponentialverteilung ist eine Wahrscheinlichkeitsverteilung zur Bestimmung zufälliger Zeitintervalle. Sie wird meist für Warte- oder Ausfallzeiten verwendet, wie zum Beispiel die Länge eines Telefongesprächs, den radioaktiven Zerfall von Atomen oder die Lebensdauer deines Handys.
Sie ist die stetige Version der geometrischen Verteilung. Beide sind exponentiell fallende Funktionen.
Exponentialverteilung Formel
Hierbei ist klar, dass die Verteilung nur für alle positiven reellen Zahlen definiert ist, schließlich sind negative Zeiten nicht möglich.
In der Statistik wird die Exponentialverteilung so abgekürzt:
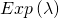
Du siehst, 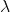 ist unser einziger Parameter. Im Folgenden gehen wir genauer auf die konkreten Formeln zur Berechnung der Wahrscheinlichkeiten ein.
ist unser einziger Parameter. Im Folgenden gehen wir genauer auf die konkreten Formeln zur Berechnung der Wahrscheinlichkeiten ein.
Dichte Exponentialverteilung
Die folgende Schreibweise der Dichtefunktion wirkt auf den ersten Blick eher unübersichtlich, ist aber nur in dieser Form zu 100% mathematisch korrekt. Das liegt daran, dass die Exponentialverteilung nur die Wahrscheinlichkeit positiver, reeler Zahlen betrachtet.
Die Dichtefunktion sieht wie folgt aus:
Dichtefunktion: 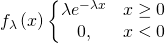
Verteilungsfunktion Exponentialverteilung
Ebenso wie bei der Dichtefunktion lassen sich Wahrscheinlichkeiten mit der kumulierten Verteilungsfunktion in diesem Zusammenhang nur für Werte aus dem positiven Bereich berechnen.
Verteilungsfunktion: 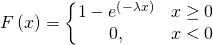
Exponentialverteilung Erwartungswert
Aus dem Erwartungswert geht hervor, dass ein großes Lamda ein kleines durchschnittliches Zeitintervall zur Folge hat und aus dem Modus, dass die Dichtefunktion ihr Maximum bei null hat. Das macht auch Sinn, denn am Beginn der Zeitmessung ist die Wahrscheinlichkeit, dass beispielsweise dein Handy noch funktioniert, am höchsten. Zusätzlich listen wir dir hier noch die wichtigsten Maße auf:
Exponentialverteilung Wahrscheinlichkeit berechnen
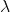 ist hier die Ausfallrate. Pro Tag geben also 0,1 Prozent der Handys ihren Geist auf. Das bedeutet, dass durchschnittlich alle 1000 Tage nach der Inbetriebnahme ein Gerät ausfällt.
ist hier die Ausfallrate. Pro Tag geben also 0,1 Prozent der Handys ihren Geist auf. Das bedeutet, dass durchschnittlich alle 1000 Tage nach der Inbetriebnahme ein Gerät ausfällt.
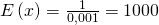
Da du dieses Jahr eine große Reise planst und dir zusätzlich kein neues Handy leisten könntest, möchtest du jetzt gerne wissen, wie wahrscheinlich es ist, dass dein Gerät noch ein weiteres Jahr funktioniert.
Wir nehmen also die Verteilungsfunktion und setzen unsere Werte ein. So kannst du die Wahrscheinlichkeit berechnen:
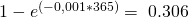
Wir sehen, nach 365 Tagen sind 30,6 Prozent der Handys ausgefallen. Die Wahrscheinlichkeit, dass deines noch funktioniert ist also bei fast 70 Prozent. Sehr gut! Deiner Reise steht quasi nichts mehr im Wege.
Gedächtnislosigkeit der Exponentialverteilung
Eine wichtige Eigenschaft dieser Wahrscheinlichkeitsverteilung ist ihre Gedächtnislosigkeit. Um bei einer gedächtnislosen Verteilung zum Beispiel die restliche Lebensdauer deines Handys zu berechnen, muss man nicht wissen, wie lange das Gerät schon im Einsatz ist. Die Wahrscheinlichkeit, dass es nach 3 Jahren die nächste Zeiteinheit überlebt ist genauso hoch, wie zu Beginn der Benutzung. Man geht davon aus, dass das Alter diese Art von Berechnungen irrelevant ist. Ist ein Bauteil mit exponentialverteilter Lebensdauer zu einem beliebigen Zeitpukt noch nicht defekt, so ist die Wahrscheinlichkeit, dass es in der nächsten Zeiteinheit noch funktionsfähig ist, genau so hoch wie anfangs. Deshalb kann man diese Verteilung nicht für die Lebenserwartung von Lebewesen anwenden, da hier das Alter auf jeden Fall eine Rolle spielt. Die Wahrscheinlichkeit, dass ein 80-jähriger weitere 50 Jahre lebt, ist viel geringer als bei einem Neugeborenen.