Gütermarkt und Konsumfunktion
Dieser Artikel behandelt die Kosumfunktion der Gütermarktnachfrage auf dem Gütermarkt in der VWL. Es erfolgt eine Erklärung der einzelnen Variablen der Funktion und das Gütermarktgleichgewicht im Gütermarktmodell wird hergeleitet und erläutert.
Bei so vielen Variablen in textform schwirrt dir schon der Kopf? Dann lass dir alles, was du zum Gütermarkt und der Konsumfunktion wissen musst, einfach und anschaulich in unserem Video erklären!
Inhaltsübersicht
Gütermarkt Makroökonomie
Der Gütermarkt in der VWL bezeichnet den Markt, auf dem Güter und Dienstleistungen gehandelt werden. Das Gütermarktmodell beschreibt die Gütermarktnachfrage, welche durch den Konsum bestimmt wird. Die Gleichung der Konsumfunktion stellt den Zusammenhang zwischen dem Konsum und dem Einkommen dar. Sie wird häufig als keynesianische Konsumfunktion nach ihrem Namensgeber John Maynard Keynes bezeichnet.
Gütermarktgleichgewicht und Konsumfunktion – Die verschiedenen Zeithorizonte der Makroökonomie
In der Makroökonomie unterscheidet man zwischen drei verschiedenen Zeithorizonten: Die kurze, die mittlere und die lange Frist. Damit du die verschiedenen Modelle verstehst, solltest du dir immer vorher klar machen, in welcher Frist du dich befindest und welche Annahmen dieser Frist zu Grunde liegen. Wir beschäftigen uns im Folgenden mit der kurzen Frist, also mit Änderungen, die sich innerhalb eines Jahres auf das Gleichgewicht auf dem Güter- und Finanzmarkt auswirken. Kurzfristig sind das Preis- und das Lohnniveau konstant und das Produktionsniveau wird von der Nachfrage bestimmt.
Gütermarktnachfrage – Vereinfachte Annahmen
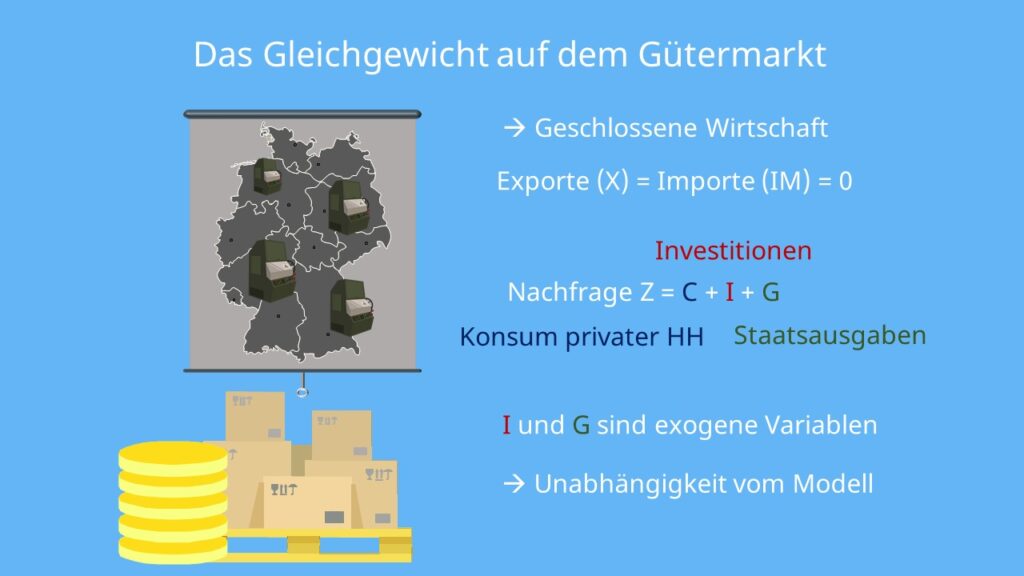
Zur Vereinfachung werden als erstes einige Annahmen getroffen. In unserer Volkswirtschaft wird nur ein Gut produziert. Dieses Gut liegt unbegrenzt und zu einem gegebenen Preis 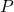 vor. Außerdem gehen wir von einer geschlossenen Wirtschaft aus, also gilt:
vor. Außerdem gehen wir von einer geschlossenen Wirtschaft aus, also gilt:
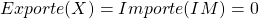
Unsere gesamte Nachfrage  setzt sich aus dem Konsum der privaten Haushalte
setzt sich aus dem Konsum der privaten Haushalte 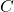 , den Investitionen
, den Investitionen 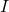 und den Staatsausgaben
und den Staatsausgaben 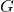 zusammen. Dadurch ergibt sich für die Gütermartknachfrage folgende Gleichung:
zusammen. Dadurch ergibt sich für die Gütermartknachfrage folgende Gleichung:
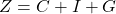
Die Staatsausgaben 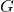 und die Investitionen
und die Investitionen 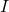 sind in unserem Gütermarktmodell vorerst exogene Variablen – das heißt ihre Werte sind gegeben und hängen nicht von unserem Modell ab.
sind in unserem Gütermarktmodell vorerst exogene Variablen – das heißt ihre Werte sind gegeben und hängen nicht von unserem Modell ab.
Konsumfunktion
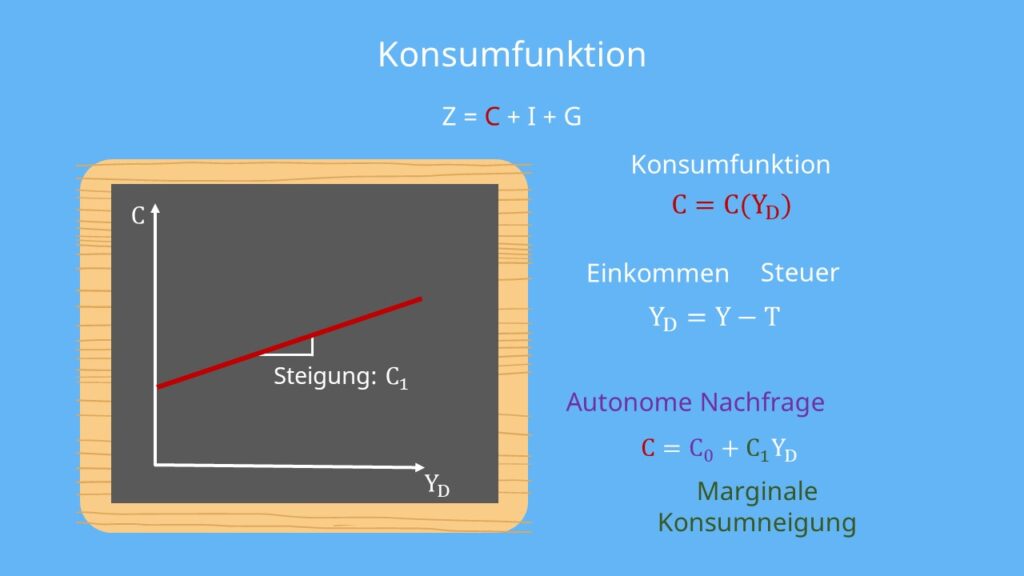
Schauen wir uns jetzt die Konsumfunktion näher an. Die Konsumfunktion ist eine steigende Funktion des verfügbaren Einkommens 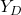 und lässt sich als
und lässt sich als 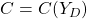 darstellen. Das verfügbare Einkommen berechnet sich aus dem Einkommen
darstellen. Das verfügbare Einkommen berechnet sich aus dem Einkommen 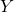 abzüglich der zu zahlenden Steuern
abzüglich der zu zahlenden Steuern 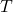 . Wir gehen von einem linearen Verlauf der Konsumfunktion aus. Die Konsumfunktion ergibt sich durch addieren der autonomen Nachfrage
. Wir gehen von einem linearen Verlauf der Konsumfunktion aus. Die Konsumfunktion ergibt sich durch addieren der autonomen Nachfrage 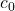 und dem Produkt aus der marginalen Konsumneigung
und dem Produkt aus der marginalen Konsumneigung 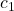 und dem verfügbaren Einkommen
und dem verfügbaren Einkommen 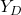 .
.
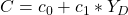
Die autonome Nachfrage 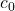 gibt den y-Achsenabschnitt unserer Konsumfunktion an und sagt aus wie viel konsumiert wird, wenn unser verfügbares Einkommen
gibt den y-Achsenabschnitt unserer Konsumfunktion an und sagt aus wie viel konsumiert wird, wenn unser verfügbares Einkommen 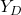 gleich
gleich 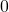 ist. Die marginale Konsumneigung
ist. Die marginale Konsumneigung 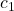 ist die Steigung unserer Geraden.
ist die Steigung unserer Geraden.
Marginale Konsumneigung hört sich kompliziert an, ist aber eigentlich ganz einfach. Nehmen wir an, dass 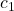 gleich 0,6 ist. Das bedeutet: wenn unser verfügbares Einkommen um 1€ steigt, erhöht sich unser Konsum um 0,6 mal 1€, also um 60 Cent. Dabei ist noch zu beachten, dass
gleich 0,6 ist. Das bedeutet: wenn unser verfügbares Einkommen um 1€ steigt, erhöht sich unser Konsum um 0,6 mal 1€, also um 60 Cent. Dabei ist noch zu beachten, dass 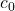 immer größer als 0 sein muss und
immer größer als 0 sein muss und 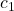 immer zwischen 0 und 1 liegen muss.
immer zwischen 0 und 1 liegen muss.
Gütermarkt Gleichgewichtsbedingung
Nachdem die Konsumfunktion behandelt wurde, schauen wir uns im Folgenden die Gleichgewichtsbedingung auf dem Gütermarkt an. Dazu brauchen wir wieder unsere Nachfragefunktion 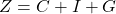 . Für den Konsum
. Für den Konsum 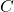 setzen wir unsere Konsumfunktion ein. Zudem setzen wir noch die Funktion für das verfügbare Einkommen
setzen wir unsere Konsumfunktion ein. Zudem setzen wir noch die Funktion für das verfügbare Einkommen 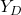 ein und schon erhalten wir unsere neue Nachfragefunktion:
ein und schon erhalten wir unsere neue Nachfragefunktion:
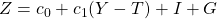
Um nun ein Gleichgewicht auf dem Gütermarkt zu erreichen, nehmen wir an, dass die Produktion genau der Nachfrage entspricht. Da in unserem Modell Einkommen und Produktion genau das gleiche sind, schreiben wir für Produktion genau wie für Einkommen den Buchstaben 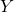 . Unsere Gleichgewichtsbedingung lautet also: Produktion
. Unsere Gleichgewichtsbedingung lautet also: Produktion 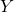 gleich Nachfrage
gleich Nachfrage  .
.
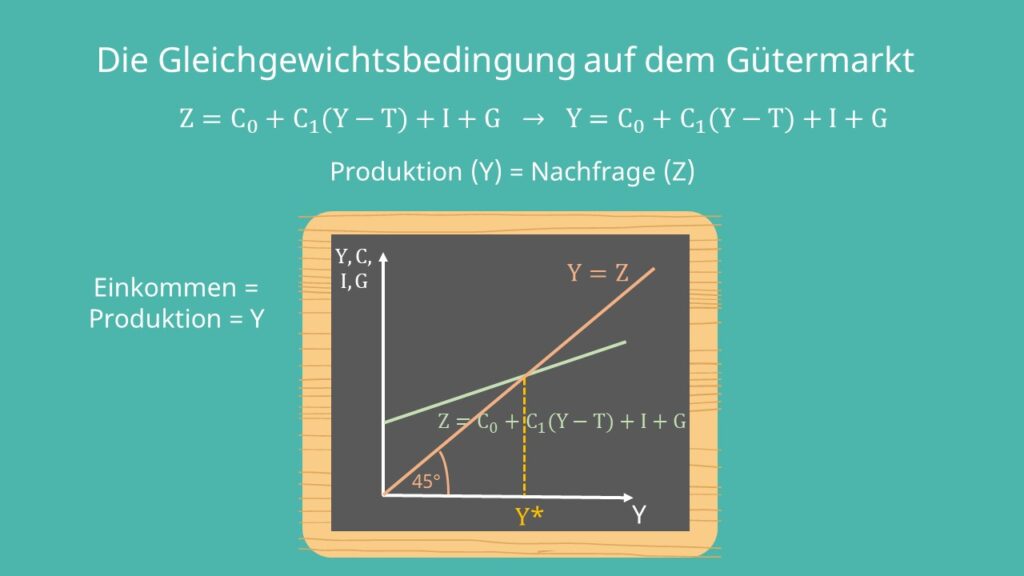
Setzen wir jetzt für die Nachfrage  unsere Nachfragefunktion ein, erhalten wir folgende Gleichung:
unsere Nachfragefunktion ein, erhalten wir folgende Gleichung:
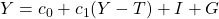
Unsere Gleichgewichtsbedingung wird in der Grafik nun als Gerade mit einer Steigung von 1, also im 45-Grad Winkel, dargestellt. Der Schnittpunkt aus der Geraden der Gleichgewichtsbedingung und der Nachfragefunktion liefert uns unsere gleichgewichtige Produktion 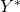 .
.
Kommt es zu einer Senkung oder Erhöhung der Staatsausgaben in Folge einer kontraktiven oder expansiven Fiskalpolitik , oder zu Investitionen in Unternehmen, verschiebt sich das Gleichgewicht auf dem Gütermarkt. Der Multiplikatoreffekt veranschaulicht diese Veränderung und gibt an, wie sich das Gesamteinkommen oder die Gesamtnachfrage durch sich gegenseitig verstärkende Faktoren verändern.