Pearson Korrelation
Hier erklären wir dir die Pearson Korrelation einfach und verständlich. Es wird geklärt wie und wann die Korrelation nach Pearson berechnet wird. Im Anschluss erfolgt die Interpretation des Korrelationskoeffizienten, welcher zuvor mit Hilfe der Pearson Korrelation Formel bestimmt wurde.
Wie du Berechnungen zur Bravais Pearson Korrelation mit Bravour meistern kannst, erfährst du auch in unserem verständlichen Video zum Pearson Korrelationskoeffizient !
Inhaltsübersicht
Korrelation nach Pearson
Die Pearson Korrelation ist eine einfache Möglichkeit, den linearen Zusammenhang zweier Variablen zu bestimmen. Dabei dient der Korrelationskoeffizient nach Pearson als Maßzahl für die Stärke der Korrelation der intervallskalierten Merkmale und nimmt Werte zwischen -1 und 1 an .
Pearson Korrelation Voraussetzungen
Merk‘ dir, dass der Bravais Pearson Korrelationskoeffizient nur lineare Zusammenhänge erkennen kann. Sind zwei Variablen also scheinbar unkorreliert, kann immer noch ein nichtlinearer, also beispielsweise ein exponentieller oder quadratischer, Zusammenhang bestehen. Außerdem ist seine Berechnung nur bei kardinalskalierten Daten möglich.
Pearson Korrelation Formel
Dann kommen wir jetzt zur Berechnung des Koeffizienten. Dafür gibt es zwei verschiedene Formeln, die ziemlich lang sind und auf den ersten Blick nicht besonders einladend aussehen. Deshalb werden wir sie Schritt für Schritt an einem Beispiel aufdröseln.
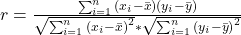
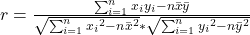
Wir betrachten also die beiden Variablen x und y, mit den drei folgenden Ausprägungen:
Zuerst berechnen wir das arithmetische Mittel von x und y:
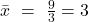
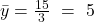
Anschließend berechnen wir die einzelnen Quadrate und das Produkt aus x und y:
Zum Schluss setzen wir die berechneten Werte noch ein. In diesem Beispiel werden wir die zweite Formel verwenden. Da wir drei Ausprägungen haben, ist n hier 3:
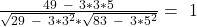
Was dieses Ergebnis von eins bedeutet, wird dir im Folgenden erklärt .
Pearson Korrelation Interpretation
Der Korrelationskoeffizient nach Person liegt stets zwischen eins und minus eins, wobei eins einen perfekt positiven und minus eins eine perfekt negative Korrelation impliziert. Man schreibt also:
![Rendered by QuickLaTeX.com r\ \in\left[-1;+1\right]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-9304c448773fd54eaf783610c793e4fb_l3.png)
Es gibt also verschiedene Szenarien, auf die wir hier eingehen.
-
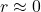 : Erhältst du ein Ergebnis von ungefähr null sind die Variablen unkorreliert.
: Erhältst du ein Ergebnis von ungefähr null sind die Variablen unkorreliert.
Das heißt, zwischen ihnen besteht kein linearer Zusammenhang. Ein Beispiel hierfür wäre, wenn man versucht einen Zusammenhang zwischen und Autokennzeichen und Körpergröße zu finden.
-
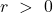 : Ist der Wert von r größer als 0, dann nennt man das eine positive Korrelation. Das bedeutet, dass größere Werte von X auch mit größeren Werten von Y einher gehen. Hier könnte man den Zusammenhang zwischen der Körpergröße eines Menschen und der Schuhgröße dieser Person hernehmen.
: Ist der Wert von r größer als 0, dann nennt man das eine positive Korrelation. Das bedeutet, dass größere Werte von X auch mit größeren Werten von Y einher gehen. Hier könnte man den Zusammenhang zwischen der Körpergröße eines Menschen und der Schuhgröße dieser Person hernehmen.
-
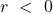 : Zuletzt betrachten wir noch den Fall, dass der Wert von r kleiner als Null ist, es sich also um einen negativen Zusammenhang handelt. Anders als bei der positiven Korrelation fallen hier die Werte von Y mit steigenden X-Werten. Hier könnte man sagen, dass je mehr Kilometer man mit dem Auto zurücklegt, desto weniger Benzin ist im Tank.
: Zuletzt betrachten wir noch den Fall, dass der Wert von r kleiner als Null ist, es sich also um einen negativen Zusammenhang handelt. Anders als bei der positiven Korrelation fallen hier die Werte von Y mit steigenden X-Werten. Hier könnte man sagen, dass je mehr Kilometer man mit dem Auto zurücklegt, desto weniger Benzin ist im Tank.
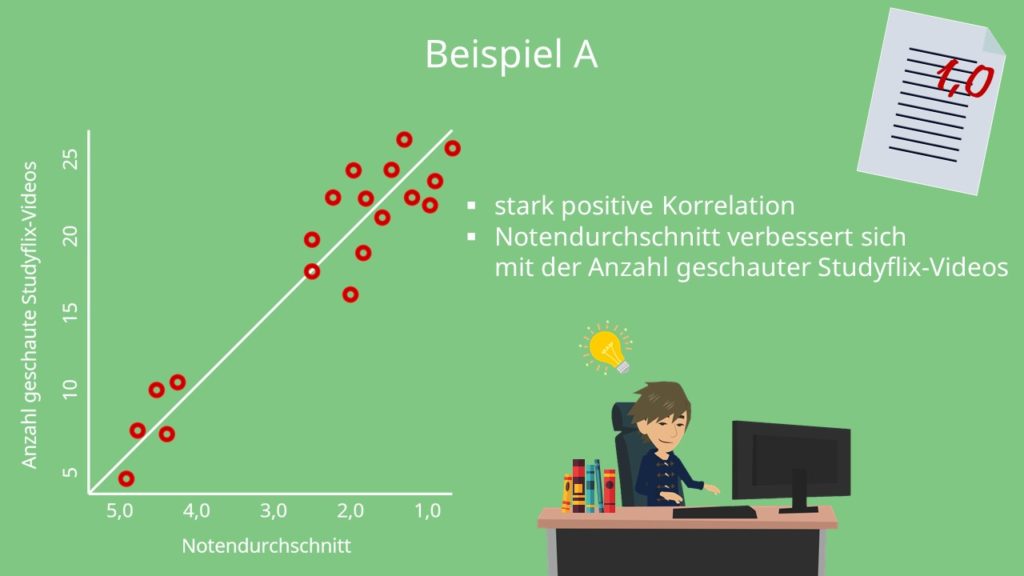
Um den Korrelationskoeffizient zu veranschaulichen, bedient man sich sogenannter Streudiagramme: Das sind Diagramme, in die die verschiedenen Stichprobendaten punktweise eingetragen werden, um den Streuungsverlauf zu beurteilen.
Hier besteht eine stark positive Korrelation. Dein Notenschnitt verbessert sich also mit der Anzahl der geschauten Studyflix Videos.
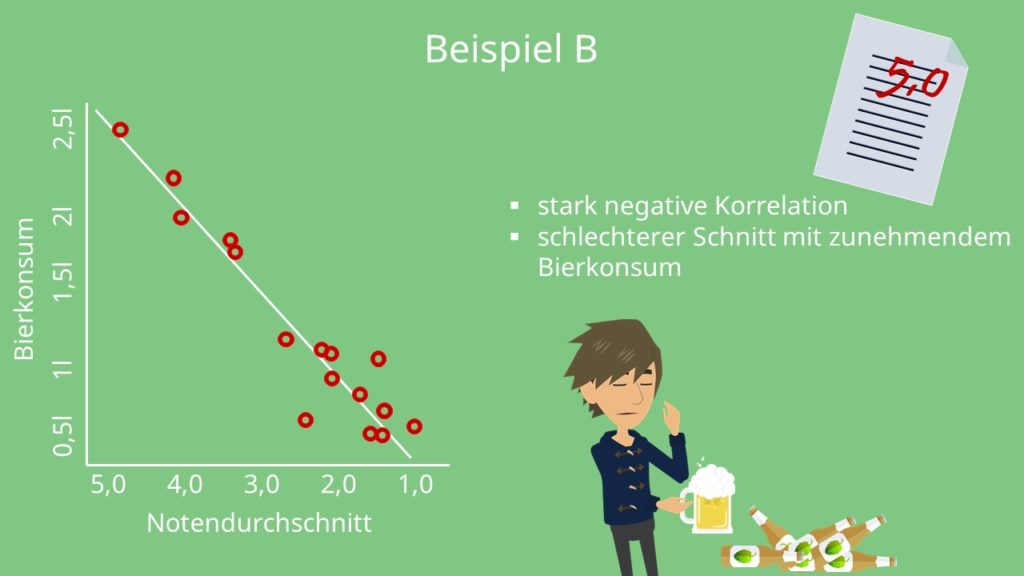
Der genau umgekehrte Zusammenhang, also eine negative Korrelation besteht in Beispiel B. Je mehr Bier du konsumierst, desto schlechter wird dein Schnitt.
Unser Ergebnis der Berechnung von eins bedeutet also, dass die beiden Variablen perfekt positiv korreliert sind und sich in die gleiche Richtung entwickeln.
Der Zusammenhang mit der Kovarianz
Ein Begriff, den du häufig in Zusammenhang mit der Korrelation hören wirst, ist die Kovarianz. Hierbei handelt es sich um die unstandardisierte Version der Korrelation.
Die Formel für die Kovarianz lautet:
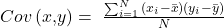
Hier summieren wir das Produkt der Differenzen zwischen den jeweiligen Zufallsvariablen und den Mittelwerten und Teilen durch N. N ist die Stichprobengröße.
Das heißt, aus dem Wert der Kovarianz lassen sich nur schwer Schlüssen ziehen. Wenn man aber nun diese mit Hilfe der Standardabweichung
standardisiert, ist dies leichter möglich.
Also kannst du dir merken: Korrelation ist die standardisierte Kovarianz.
Hier die wichtigsten Dinge die du beachten musst
- Überblick behalten
- Zwischenergebnisse beachten
- Tabellenschreibweise einhalten
Du siehst, die Berechnung ist eigentlich gar nicht so schwer. Die Kunst ist es, bei vielen Ausprägungen, den Überblick zu behalten und immer mit den richtigen Zwischenergebnissen weiter zu rechnen. Deshalb kann zum Beispiel eine Tabellenschreibweise, wie wir sie gerade verwendet haben sehr hilfreich sein.