Lineare Optimierung
Die lineare Optimierung wird in vielen verschiedenen Bereichen eingesetzt. In der Vorlesung wird das Thema lineare Optimierung oft sehr komplex erklärt. Mit unserer Anleitung zeigen wir dir Schritt für Schritt, wie du das Problem der linearen Optimierung lösen kannst.
Inhaltsübersicht
Lineare Optimierung Erklärung
Die lineare Optimierung wird auch als lineare Programmierung bezeichnet und ist ein mathematisches Verfahren, welches in vielen Bereichen zum Einsatz kommt. Einer davon ist die Produktion & Logistik. Die lineare Optimierung beschäftigt sich im Grunde mit der Maximierung oder Minimierung einer linearen Funktion unter Nebenbedingungen. Die zu maximierende Funktion ist dir mit Sicherheit bereits unter dem Namen der Zielfunktion bekannt. Die lineare Optimierung besteht aus drei Teilen:
- der Zielfunktion: diese kann beispielsweise ein maximaler Erlös sein
- der Nebenbedingungen (Restriktionen): der gesuchte maximale Erlös ist z.B. durch deine Maschinenkapazität beschränkt
- die Nichtnegativitätsbedingung: die Entscheidungsvariablen der linearen Optimierung dürfen nur größer oder gleich null sein.
Die lineare Optimierung ist in der Produktion & Logistik vielseitig einsetzbar. Sie löst Produktions- und Transportprobleme und führt im besten Fall zu einer oder mehreren optimalen Lösungen. Es kann allerdings auch vorkommen, dass durch die Berechnung keine optimale Lösung gefunden wird, wenn diese beispielsweise gar nicht existiert.
Lineare Optimierung Beispiel: Produktionsprogrammplanung
Wie du bereits erfahren hast, wird die lineare Programmierung auch bei der mittelfristigen operativen Produktionsprogrammplanung angewendet, um den größtmöglichen Gewinn zu erzielen. Dazu schauen wir uns im Folgenden ein Beispiel an.
In unserem Beispiel möchtest du genau so viele Kleider und T-Shirts produzieren, um den maximalen Deckungsbeitrag zu erhalten. Daher steht 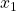 für die Anzahl der Kleider und
für die Anzahl der Kleider und 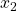 für die Anzahl der T-Shirts. Um die idealen Produktionsmengen für
für die Anzahl der T-Shirts. Um die idealen Produktionsmengen für 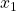 und
und 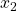 herauszufinden, wenden wir die lineare Optimierung an.
herauszufinden, wenden wir die lineare Optimierung an.
Zielfunktion für die Lineare Optimierung Aufgaben
Nehmen wir an, du erzielst mit jedem verkauften Kleid einen Gewinn von sieben Geldeinheiten (GE) und mit jedem verkauften T-Shirt einen Gewinn von vier GE. Jetzt können wir in einem ersten Schritt unsere Zielfunktion für die lineare Optimierung aufstellen.
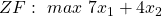
Nebenbedingungen für die lineare Optimierung
Jetzt kannst du natürlich nicht unendlich viel produzieren, da deine Kapazitäten und die Nachfrage am Markt begrenzt sind. Neben unserer Zielfunktion müssen wir also mehrere Nebenbedingungen beachten, um die lineare Optimierung durchzuführen. Nehmen wir an du kannst im Planungszeitraum maximal zehn Kleider und 20 T-Shirts am Markt absetzen. Mit diesen Informationen kannst du nun die zwei folgenden Restriktionen für die lineare Programmierung aufstellen:
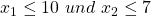
Auch die Maschine, die bei der Produktion im Einsatz ist, hat ihre Grenzen. Nehmen wir an ihre Kapazität beträgt im Planungszeitraum insgesamt 15 Zeiteinheiten (ZE). Du weißt, dass die Produktion eines Kleides an der Maschine drei ZE beträgt und die Produktion eines T-Shirts zwei ZE. Damit kannst du eine weitere Nebenbedingung für die lineare Optimierung aufstellen:
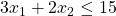
Jetzt kommt noch die zeitliche Beschränkung durch das Personal hinzu. Nehmen wir an wir haben 20 ZE zur Verfügung. Die Produktion eines Kleides benötigt sechs ZE Personal, die eines T-Shirts zwei ZE. Daraus ergibt sich diese Nebenbedingung für die Lineare Optimierung:
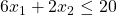
Zuletzt ergeben sich noch zwei Nebenbedingungen aus der Nichtnegativitätsbedingung. Diese sorgt dafür, dass die Anzahl an Kleidern und an T-Shirts nicht negativ sein kann. Wir schreiben also:
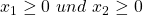
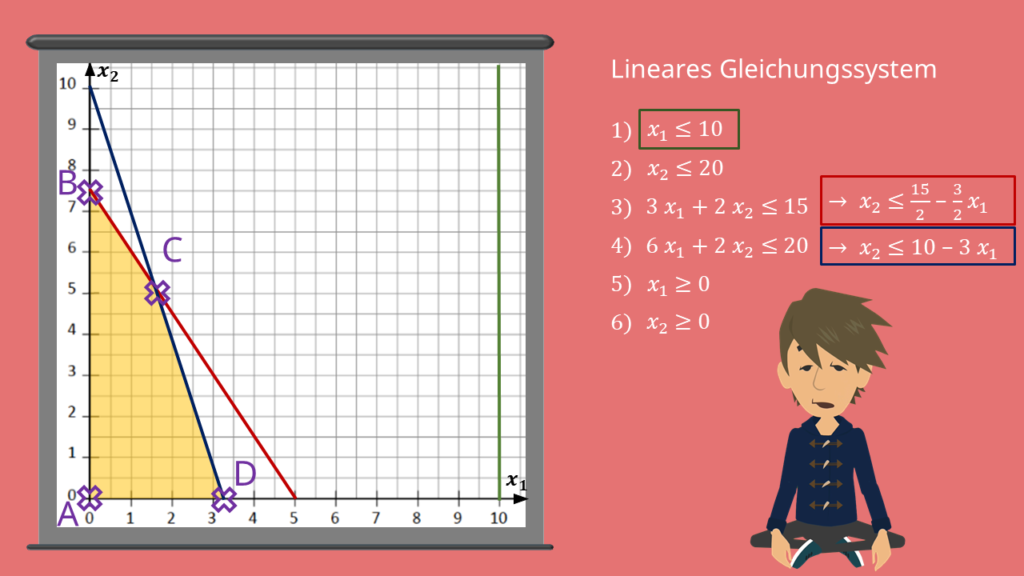
Lineares Gleichungssystem
Schauen wir uns also die Zielfunktion und die Nebenbedingungen nochmal im Überblick an. Wie du siehst, wird die Produktion durch sechs Nebenbedingungen beschränkt.
Aber wie erhältst du nun deine optimalen Produktionsmengen? Am einfachsten geht das über die graphische Lösung. Du löst also alle Nebenbedingungen nach 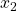 auf und erhälst ein lineares Gleichungssystem.
auf und erhälst ein lineares Gleichungssystem.
Lineare Optimierung graphische Lösung
Die einzelnen Geraden zeichnest du in ein Koordinatensystem ein. Die x-Achse gibt hier die Anzahl an Kleidern an, die y-Achse die Anzahl an T-Shirts. Das sieht dann so aus:
Auch die beiden Achsen 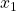 und
und 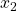 stellen Nebenbedingungen für die lineare Optimierung dar, da wir ja keine negativen Produktionsmengen erhalten dürfen. Du siehst, dass es mithilfe des linearen Gleichungssystems zu vier Schnittpunkten kommt. So erhalten wir die vier Ecken A, B, C und D, die unseren Lösungsraum begrenzen. Dieser ist in unserer Zeichnung gelb schraffiert und beinhaltet alle möglichen Lösungen. Die optimale Lösung wird sich in einer Ecke befinden, da dort die Kapazitäten am besten genutzt werden. Aber welche Ecke gibt die optimalen Produktionsmengen an?
stellen Nebenbedingungen für die lineare Optimierung dar, da wir ja keine negativen Produktionsmengen erhalten dürfen. Du siehst, dass es mithilfe des linearen Gleichungssystems zu vier Schnittpunkten kommt. So erhalten wir die vier Ecken A, B, C und D, die unseren Lösungsraum begrenzen. Dieser ist in unserer Zeichnung gelb schraffiert und beinhaltet alle möglichen Lösungen. Die optimale Lösung wird sich in einer Ecke befinden, da dort die Kapazitäten am besten genutzt werden. Aber welche Ecke gibt die optimalen Produktionsmengen an?
Lineare Optimierung graphisch – Maximierung der Zielfunktion
Dazu musst du in einem letzten Schritt für die lineare Optimierung die Zielfunktion in dein Koordinatensystem eintragen. Dafür setzt du sie zuerst gleich null und löst sie dann nach 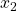 auf:
auf:
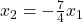
Diese zeichnest du in dein Koordinatensystem ein. Du siehst, die Zielfunktion ist noch variabel. Wir möchten ihren Wert ja maximieren. Deshalb schiebst du die Gerade deiner Zielfunktion nun so weit nach oben rechts bis sie die letzte Ecke deines zulässigen Bereichs schneidest.
Jetzt musst du nur noch die Koordinaten ablesen und schon hast du die optimalen Produktionsmengen gefunden. Du musst also etwa 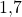 Kleider und etwa
Kleider und etwa 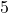 T-Shirts produzieren, um den maximalen Gewinn zu erhalten.
T-Shirts produzieren, um den maximalen Gewinn zu erhalten.
Rechnerische Überprüfung der grafischen Lösung
Möchtest du die graphische Lösung überprüfen, kannst du die Zielfunktionswerte jeder Ecke berechnen. Da unser Zielfunktionswert unseren Gewinn angibt, werden wir die Ecke mit dem höchsten Wert wählen. Damit du die Zielfunktionswerte ausrechnen kannst, musst du die Koordinaten jeder Ecke kennen. Das bereits aufgestellte lineare Gleichungssystem hilft uns dabei.
Beginnen wir mit der Ecke A. Die Koordinaten sind hier offensichtlich 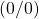 . Dementsprechend ist der Zielfunktionswert auch null. Die Ecke B ist der Schnittpunkt der
. Dementsprechend ist der Zielfunktionswert auch null. Die Ecke B ist der Schnittpunkt der 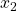 -Achse mit der Geraden drei. Wir können die Werte also ganz einfach ablesen:
-Achse mit der Geraden drei. Wir können die Werte also ganz einfach ablesen: 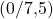 . Setzten wir die Werte in die Zielfunktion ein, kommen wir auf 30.
. Setzten wir die Werte in die Zielfunktion ein, kommen wir auf 30.
Weiter geht’s mit der Ecke C. Hier schneiden sich die Geraden drei und vier. Um ihre Koordinaten herauszufinden, müssen wir beide Geraden miteinander gleichsetzen. Lösen wir nach 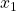 auf, erhalten wir etwa
auf, erhalten wir etwa 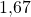 . Setzen wir diesen Wert in eine der beiden Geradengleichungen ein, kommen wir für
. Setzen wir diesen Wert in eine der beiden Geradengleichungen ein, kommen wir für 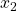 auf
auf 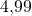 . Setzen wir beide Werte dann in die Zielfunktion ein, erhalten wir
. Setzen wir beide Werte dann in die Zielfunktion ein, erhalten wir 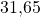 .
.
Jetzt fehlt nur noch die Ecke D. Hier schneidet die Gerade vier die 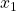 -Achse. Setzen wir in die Geradengleichung für
-Achse. Setzen wir in die Geradengleichung für 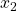 null ein, erhalten wir für
null ein, erhalten wir für 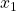 ungefähr
ungefähr 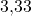 . Hier bekommen wir dann einen Zielfunktionswert von
. Hier bekommen wir dann einen Zielfunktionswert von 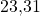 .
.
Vergleich der Zielfunktionswerte
Vergleichen wir alle Werte miteinander, sehen wir, dass die Ecke C mit 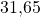 den höchsten Wert besitzt. Wir sind bei der graphischen Lösung also genau richtig gelegen.
den höchsten Wert besitzt. Wir sind bei der graphischen Lösung also genau richtig gelegen.
Durch die Berechnungen konnten wir ebenfalls die exakt zu produzierende Mengen an Kleidern und T-Shirts herausfinden, nämlich 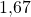 Kleider und
Kleider und 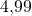 T-Shirts. Die lineare Optimierung führt also sowohl graphisch als auch rechnerisch zur richtigen Lösung.
T-Shirts. Die lineare Optimierung führt also sowohl graphisch als auch rechnerisch zur richtigen Lösung.