Spielbaum
Der Spielbaum ist ein wichtiges Hilfsmittel, um im Rahmen von dynamischen Spielen einfach strategische Entscheidungen zu treffen. Die Besonderheit bei dynamischen Spielen ist, dass die Spieler ihre Entscheidungen nacheinander treffen. Die Wahl der anderen Spieler ist also zum Zeitpunkt der eigenen Entscheidung beobachtbar. Im Folgenden erklären wir euch den Spielbaum anhand eines einfachen Beispiels.
Mal wieder ein langer und ausführlicher Artikel, geht das nicht einfacher? Doch, wir haben einen Trick wie du das Thema im Nu verstehst: Schau dir unser Video dazu an!
Inhaltsübersicht
Spielbaum: Beispiel und Vorgehen
Um den Aufbau des Spielbaums besser zu verstehen und im Anschluss dann zu einem Gleichgewicht zu gelangen nehmen wir uns folgendes Beispiel zur Hilfe: die Altersversorgung Deiner Eltern. Diese können sich entscheiden ob sie heute viel konsumieren und nur wenig sparen oder wenig konsumieren und viel sparen. Auch Du und Deine Geschwister können sich für eine der zwei Handlungen entscheiden. Ihr habt die Wahl ob ihr eure Eltern im Alter finanziell unterstützt oder nicht. Hier gibt es jetzt zum ersten Mal eine zeitliche Struktur. Es entscheiden sich also erst eure Eltern ob sie viel oder wenig sparen und dann legt ihr euch fest, ob ihr sie unterstützt.
Spielbaum als Extensivform
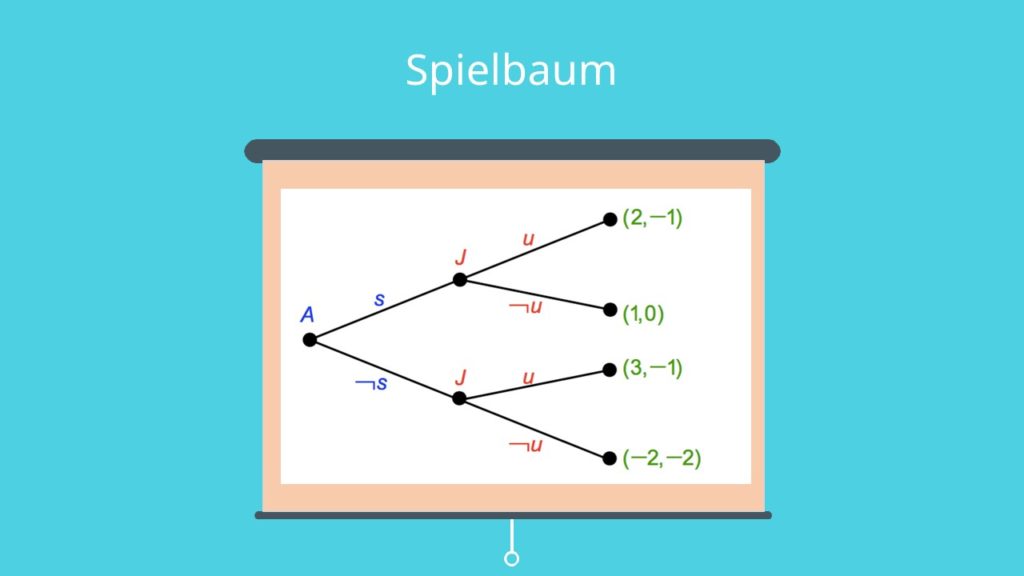
Ihr könnt somit die Sparentscheidung eurer Eltern beobachten und dann im Nachhinein für euch passend reagieren. Durch die zeitliche Struktur kann man das Beispiel nicht einfach in einer Matrix abbilden, da die Zeit so nicht mehr erkennbar wäre. Es muss also ein anderer Weg gefunden werden. Meist verwendet man für die Darstellung einen Spielbaum, der auch als Extensivform von Spielen bekannt ist. In unserem Fall könnte er so aussehen:
Im Spielbaum steht also A für Deine Eltern und J für Dich und Deine Geschwister. Die Entscheidung Deiner Eltern wird mit s für sparen und 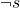 für nicht sparen gekennzeichnet. Die Wahl von Dir und Deinen Geschwistern wird mit u für unterstützen und
für nicht sparen gekennzeichnet. Die Wahl von Dir und Deinen Geschwistern wird mit u für unterstützen und 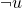 für nicht unterstützen symbolisiert. Am Ende jedes Astes des Spielbaums stehen die Auszahlungen: An erster Stelle die Deiner Eltern und an zweiter Stelle die von Dir und deinen Geschwistern. Der Spielbaum wird mit Hilfe von Rückwärtsinduktion ausgewertet, dabei gehst du vom letzten Ergebnis aus bis an den Anfang des extensiven Spiels und kannst so die richtige Entscheidung ablesen.
für nicht unterstützen symbolisiert. Am Ende jedes Astes des Spielbaums stehen die Auszahlungen: An erster Stelle die Deiner Eltern und an zweiter Stelle die von Dir und deinen Geschwistern. Der Spielbaum wird mit Hilfe von Rückwärtsinduktion ausgewertet, dabei gehst du vom letzten Ergebnis aus bis an den Anfang des extensiven Spiels und kannst so die richtige Entscheidung ablesen.
Gleichgewichte im Spielbaum
Darüber hinaus müssen wir uns erstmal über die Handlungsmöglichkeiten klarwerden. Bei den Eltern ist das einfach, sie können nur zwischen sparen und nicht sparen wählen. Aber bei euch wird das schon etwas komplizierter. Wie ihr im Spielbaum seht, legt ihr euch NACH euren Eltern fest und habt insgesamt vier verschiedene Entscheidungsmöglichkeiten: in jedem Fall unterstützen; nur unterstützen, wenn die Eltern nicht sparen; nur unterstützen, wenn die Eltern sparen oder nie unterstützen. Mit diesen Beobachtungen können wir nun den Spielbaum in eine Tabelle überführen:
In der obersten Zeile sind die Handlungsmöglichkeiten von Dir und Deinen Geschwistern eingetragen und links die eurer Eltern. Wenn wir uns die Tabelle genau anschauen, sehen wir, dass wir insgesamt drei Nash-Gleichgewichte haben: Wenn die Eltern nicht sparen, ist es für euch am besten sie zu unterstützen, da  . Wenn eure Eltern sparen, dann unterstützt ihr sie nicht und gebt damit auch hier wieder die beste Antwort auf die Strategie eurer Eltern. Im Nachhinein wollt ihr davon auch nicht mehr abweichen, weil es für Euch nur eine Verschlechterung bedeuten würde.
. Wenn eure Eltern sparen, dann unterstützt ihr sie nicht und gebt damit auch hier wieder die beste Antwort auf die Strategie eurer Eltern. Im Nachhinein wollt ihr davon auch nicht mehr abweichen, weil es für Euch nur eine Verschlechterung bedeuten würde.
Auswertung des Spielbaums
Aber was fangen wir jetzt damit an? Du und Deine Geschwister wollen am liebsten das Nash-Gleichgewicht „sparen und nie unterstützen erreichen“, da dort eure Auszahlung mit 0 noch am höchsten ist. Die andere Kombi mit 0 ist übrigens kein Nash-Gleichgewicht. Dafür müsste man auch die Unterstützung im Falle des Nichtsparens ausschließen. Das zweite u bedeutet auch beim Nichtsparen keine Unterstützung.
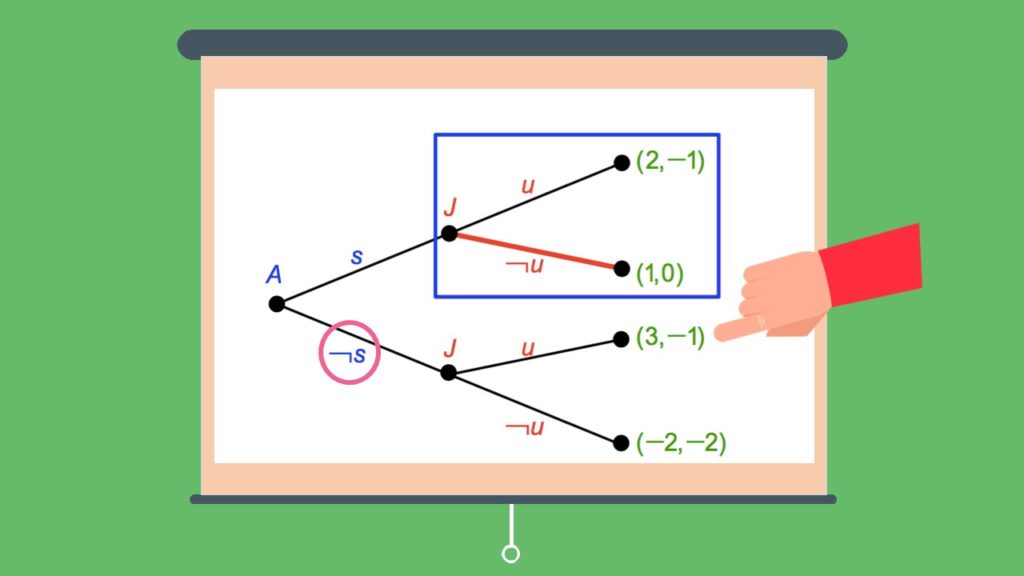
Allerdings ist die Unterstützungsverweigerung im Falle des Nichtsparens nicht glaubwürdig. Denn wir unterstellen im Nash-Gleichgewicht, dass die Spieler ihre Strategie nur einmal festlegen und danach kein Interesse mehr an einer Änderung haben. Damit schließen wir aber aus, dass Du und Deine Geschwister im Zeitverlauf lernen. Und das ist unser Problem. Schauen wir uns dafür nochmal den Spielbaum an:
Wenn eure Eltern sparen und ihr das seht, dann habt ihr kein Interesse sie zu unterstützen. Schließlich haben sie ja dann genug Geld und eure Auszahlung mit 0 ist größer als mit -1, wenn ihr sie unterstützen würdet. Wenn eure Eltern aber nicht sparen und ihr bekommt das mit, unterstützt ihr sie, da ihr eure Eltern natürlich nicht verhungern lasst und da  ist.
ist.
Das teilspielperfekte Nash-Gleichgewicht im Spielbaum
Wenn jetzt Deine Eltern ihr Sparverhalten davon abhängig machen ob ihr sie unterstützt, ist es für sie optimal nicht zu sparen. Denn wenn Ihr das seht, würdet ihr sie unterstützen und die Auszahlung eurer Eltern wäre mit 3 durch das Nichtsparen größer als mit 1 wenn sie sparen würden. Damit haben wir ein neues Gleichgewicht gefunden, bei dem der Zeitverlauf berücksichtigt ist: nicht sparen und unterstützen. Es handelt sich hier um ein sogenanntes teilspielperfekte Nash-Gleichgewicht.
Damit ist das Gleichgewicht „sparen und nicht unterstützen“ nicht zeitkonsistent, denn wenn ihr bemerkt, dass eure Eltern noch nicht gespart haben, dann werdet ihr eure Entscheidung nicht zu unterstützen auf unterstützen ändern. Damit bleibt das Gleichgewicht „nicht sparen und unterstützen“ als einzig sinnvolle Vorhersage für den Spielausgang im Spielbaum übrig.
Solltest du dir also einmal Gedanken über deine Altersversorgung machen, weißt du jetzt wie du dabei strategisch am besten vorgehen solltest. Der Spielbaum kann auch in sehr vielen anderen Situationen angewendet werden.