Transportproblem- Heuristische Verfahren
Du hast über Transportprobleme gehört, weißt aber nicht mehr wie man diese lösen kann. Keine Sorge! Im folgenden Beitrag erklären wir Dir, wie man Transportprobleme mit heuristischen Verfahren wie der Nordwesteckenregel, der Spaltenminimummethode oder mit der Vogelsche Approximation lösen kann und mit der MODI Methode diese Lösung sogar noch optimieren kann.
Inhaltsübersicht
Klassisches Transportproblem
Eine solche spezielle Struktur hat das sogenannte klassische Transportproblem. Stell dir dazu drei Produktionsstandorte eines Herstellers vor und 4 Firmen, die ein Produkt kaufen wollen. Unser Produkt ist in diesem Fall ein Computer. Die Angebotsspalte gibt vor wie viele Computer jeder Produktionsstandort liefern kann. Die Zeile „Nachfrage“ zeigt dir wie viele Computer die Firmen bestellen. Die Zahlen in der Mitte sind die Kosten, um einen Computer von der Produktion zur jeweiligen Firma zu liefern.
Der Transport von Produktion 2 nach Firma 3 kostet zum Beispiel 3 Geldeinheiten. Jetzt will der Hersteller natürlich alle produzierten Computer loswerden und sie zu den geringsten Kosten an die Firmen ausliefern. Deswegen stellt sich nun die Frage: welcher Produktionsstandort soll zu welcher Firma wie viele Computer ausliefern, um die Lieferkosten am geringsten zu halten und alle Nachfragen zu erfüllen?
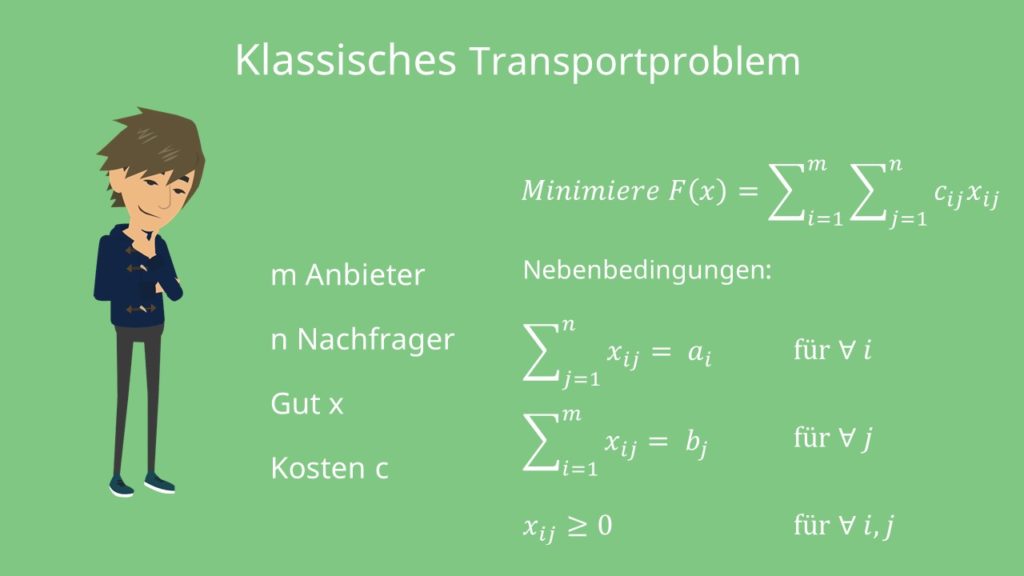
Allgemein ausgedrückt existieren m Anbieter und n Nachfrager eines Gutes x. Das Angebot der Güter wird komplett von den Nachfragern nachgefragt. Das ist die erste Nebenbedingung. Die Nachfrage des Guts wird zudem von allen Anbietern bereitgestellt. Das ist die zweite Nebenbedingung. Das Gesamtangebot entspricht also der Gesamtnachfrage. Die Zielfunktion minimiert die Kosten für den Transport mal der Transportmenge von Anbieter i zu Nachfrager j. Und natürlich dürfen keine negativen Güter produziert werden. Dies stellt unsere dritte Nebenbedingung sicher. ij bedeutet in diesem Fall von Anbieter i zu Nachfrager j. Du weißt wie viele Einheiten des Guts jeder Nachfrager benötigt und wie viel jeder Anbieter bereitstellen kann. Auch die Kosten für den Transport von Anbieter i zu Nachfrager j sind dir bekannt. Jetzt suchst du den kostenminimalen Transportplan, bei dem alle Bedarfe erfüllt werden.
Das Beispiel von eben drücken wir jetzt in Variablen aus. Um dieses Transportproblem zu lösen, wird zunächst ein Eröffnungsverfahren, eine sogenannte Heuristik angewendet. Das ist ein Näherungsverfahren, dass in kurzer Zeit zu einer zulässigen guten Basislösung führt, die aber nicht immer optimal ist. Die zulässige Basislösung führt dann mit einem Optimierungsverfahren, der sogenannten MODI-Methode, zu einer optimalen Lösung. Diese Methode zeigen wir dir dann im nächsten Video.
Nordwesteckenregel
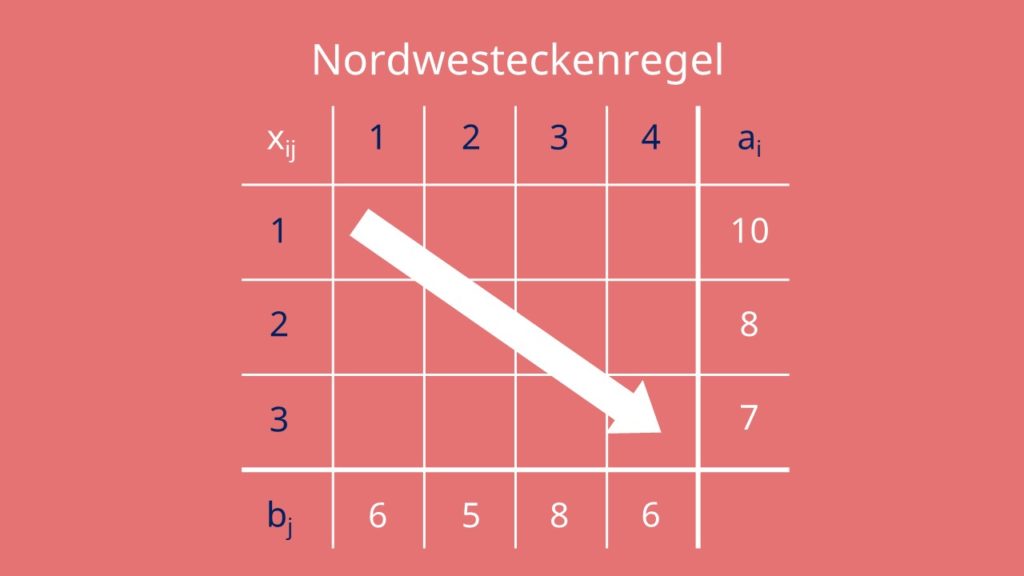
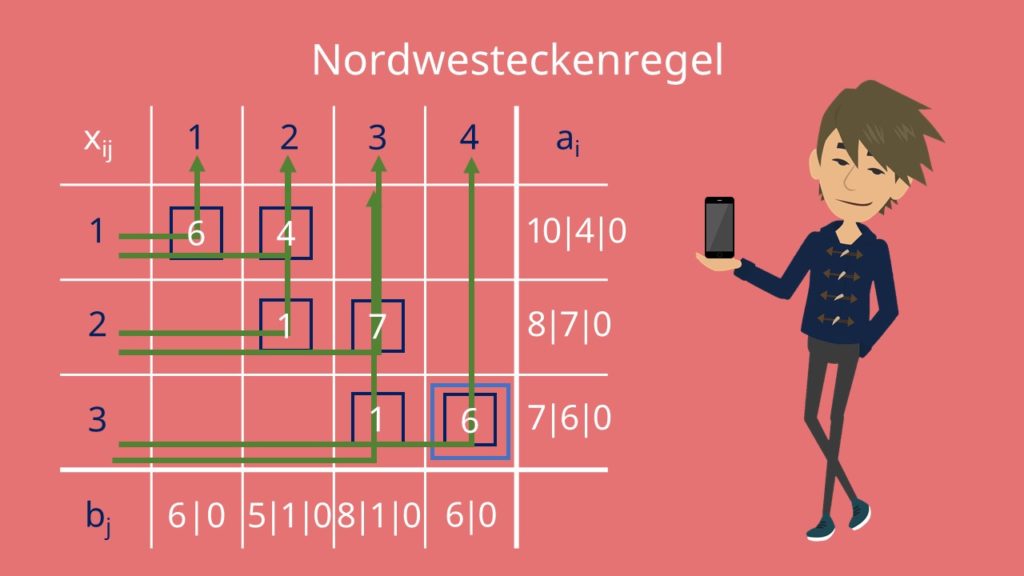
Die Nordwesteckenregel ist eine sehr einfache Heuristik. Sie berücksichtigt keine Transportkosten und ermittelt Basisvariablen im Transporttableau von links oben nach rechts unten.
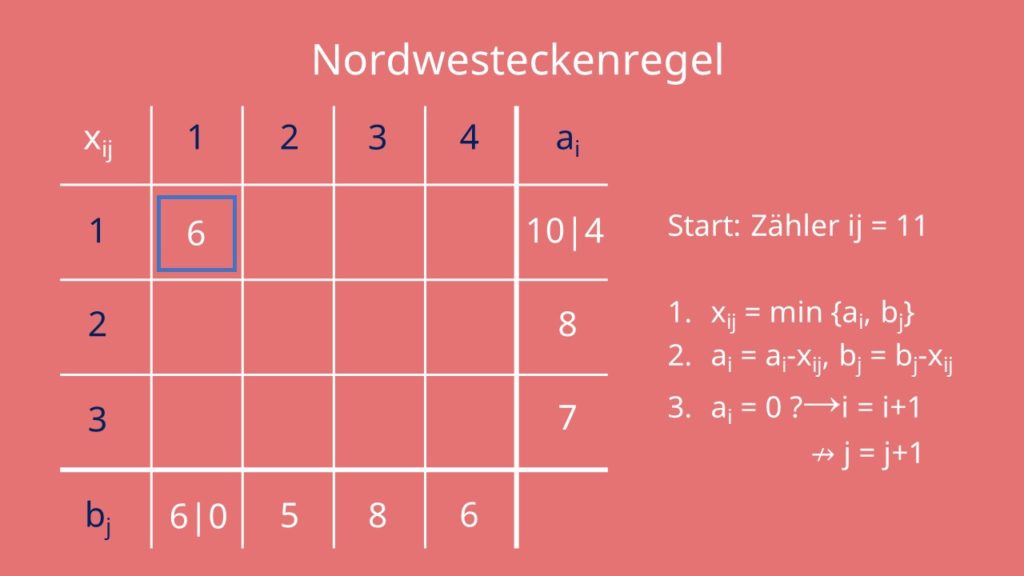
Am Anfang sind bei der Nordwesteckenregel alle Variablen xij in deinem Transporttableau erstmal 0. Deshalb kannst du die Zellen auch einfach leer lassen. Da du links oben startest, setzt du deinen Zähler für Zeile i und Spalte j gleich 1. Der Zähler zeigt dir immer an in welcher Zelle deines Transporttableaus du dich gerade befindest. Als nächstes setzt du xij, also x11, gleich dem Minimum von a1 und b1. Da das Minimum von 10 und 6, 6 ist, setzt du a11 gleich 6. Dann subtrahierst du von ai und bj dein xij. Für a1 ist das gleich „10 Minus 6 gleich 4“ und für b1 ist es gleich „6 Minus 6 gleich 0“.
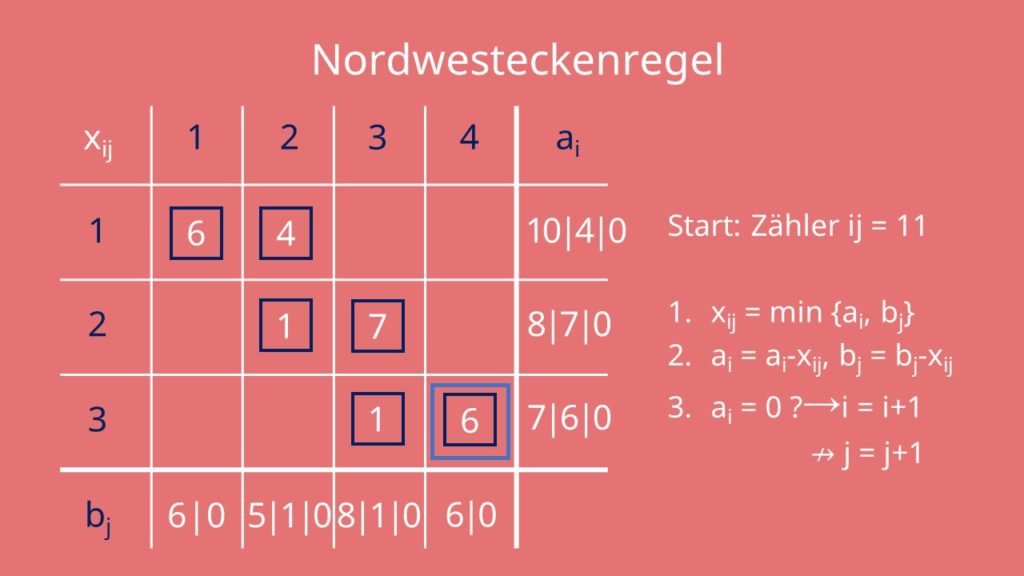
Jetzt schaust du, ob dein ai oder bj gleich 0 ist. Ist ai gleich 0, erhöhst du i deines Zählers um eins. Ist bj gleich 0, erhöhst du j deines Zählers um 1. In unserem Fall ist b1 gleich 0. Deswegen wird j um eins erhöht und ist jetzt 2. Der Zähler wandert demnach eine Zelle nach rechts. Das war eine Iteration. Du wiederholst das jetzt so oft, bis du schließlich rechts unten im Südosten angekommen bist. Dann stoppst du das Verfahren. Damit hast du eine zulässige Basislösung für die Nordwesteckenregel gefunden.
Du kannst sie jetzt so interpretieren: Anbieter 1 transportiert 6 Einheiten des Guts zu Nachfrager 1 und 4 Einheiten zu Nachfrager 2 und so weiter.
Spaltenminimummethode
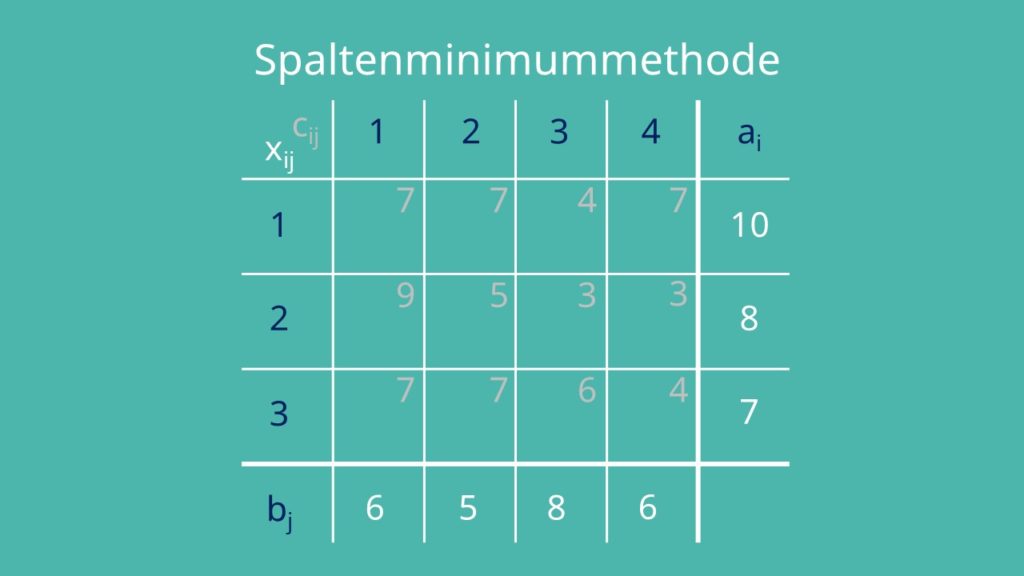
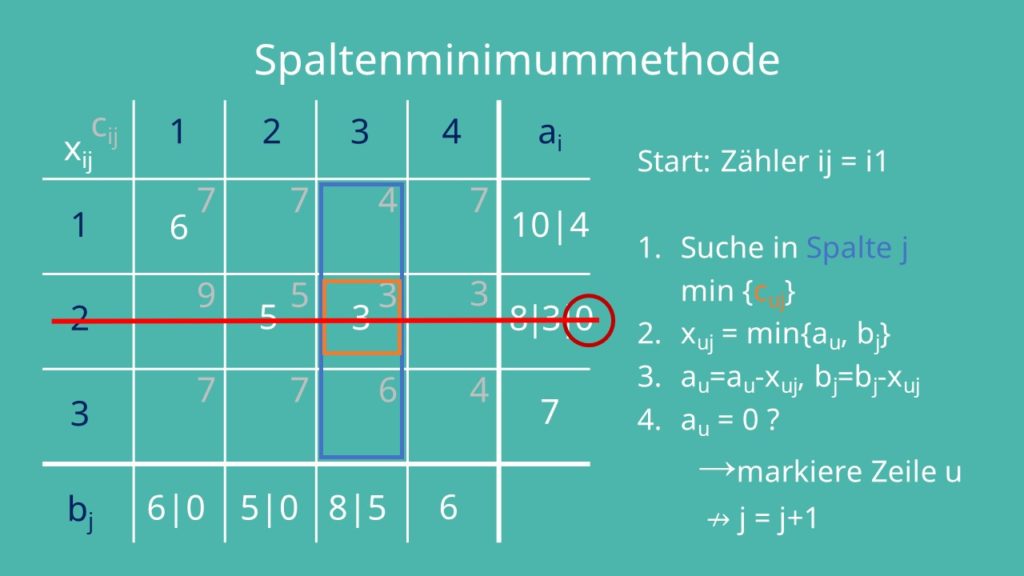
Als nächstes stellen wir dir die Spaltenminimummethode vor. Für diese Methode brauchst du zusätzlich zum Transporttableau auch noch die gegebene Kostenmatrix. Diese haben wir grau über das Transporttableau gelegt.
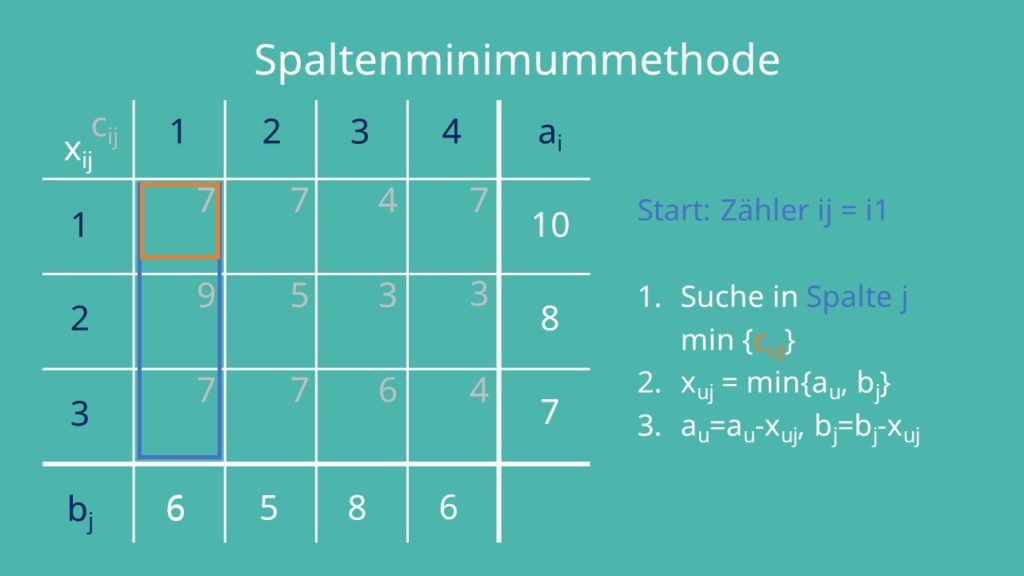
Am Anfang ist der Zähler für Spalte j gleich 1. Alle xij sind wie bei der Nordwesteckenregel 0. Du suchst in Spalte j das kleinste Element der Kostenmatrix cuj. Du siehst, dass 7 die kleinste Zahl ist, diese aber zweimal in der Spalte vorkommt. In so einem Fall ist es egal welche du nimmst, außer es ist in deiner Aufgabe vorgegeben. Wir nehmen hier c11 gleich 7. Die Variable xuj wird jetzt gleich dem Minimum von au und bj gesetzt. Wir suchen also das Minimum von von a1 und b1.
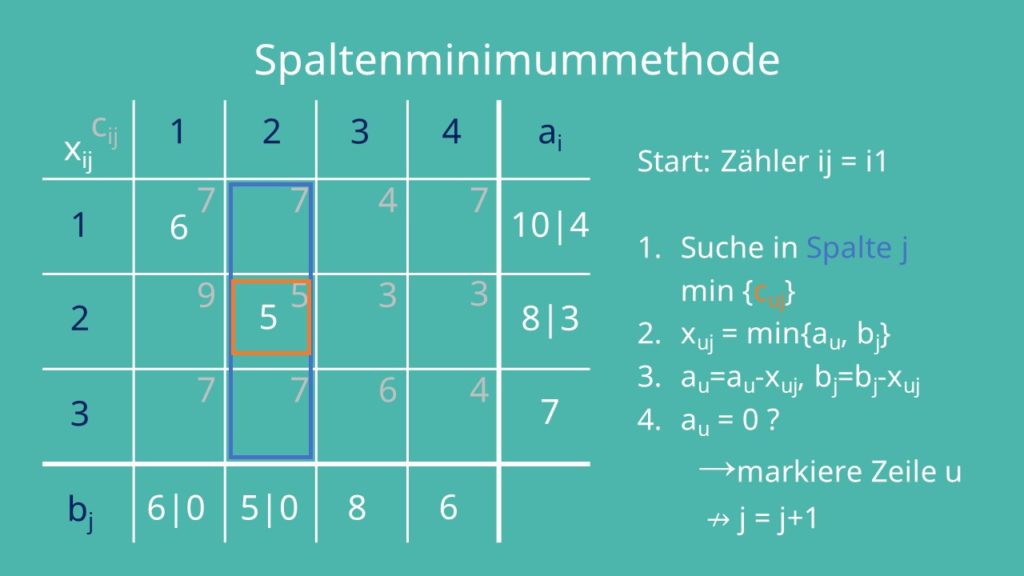
Unser xij ist somit 6. xuj wird nun von au und bj subtrahiert. Wir rechnen für a1: 10 Minus 6 gleich 4 und für b1: 6 Minus 6 gleich 0. Wenn au dadurch jetzt 0 ist, markierst du die Zeile u. Das bedeutet, du streichst sie durch und beachtest sie im Folgenden nicht mehr.
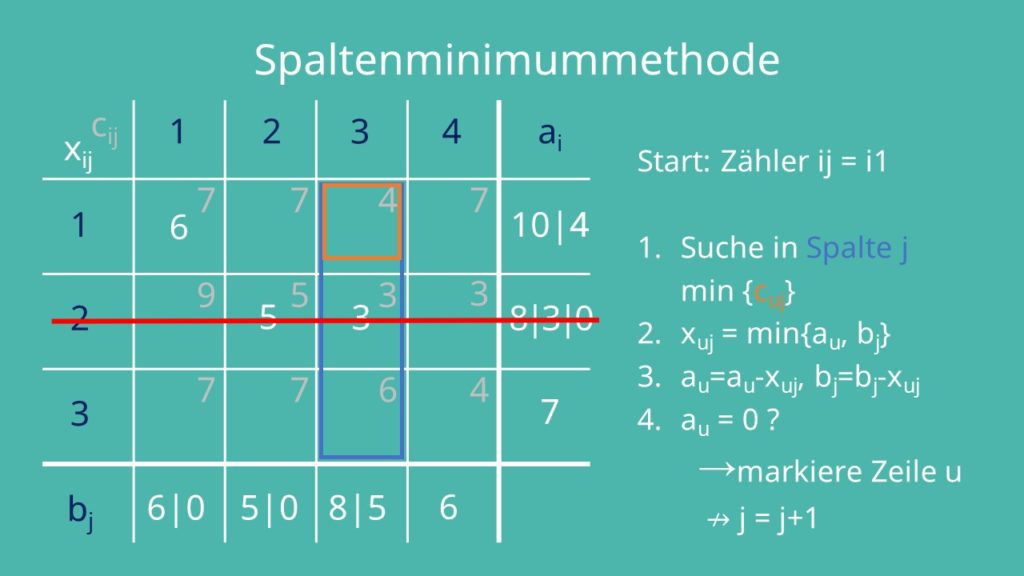
Ist dies nicht der Fall – wie in unserem Beispiel – erhöhst du j um 1. Das ist eine Iteration. Die zweite Iteration sieht so aus:
Erst in der dritten Iteration wird a2 gleich 0. Wir markieren daher Zeile 2. Für alle folgenden Iterationen darf diese Zeile nicht mehr betrachtet werden.
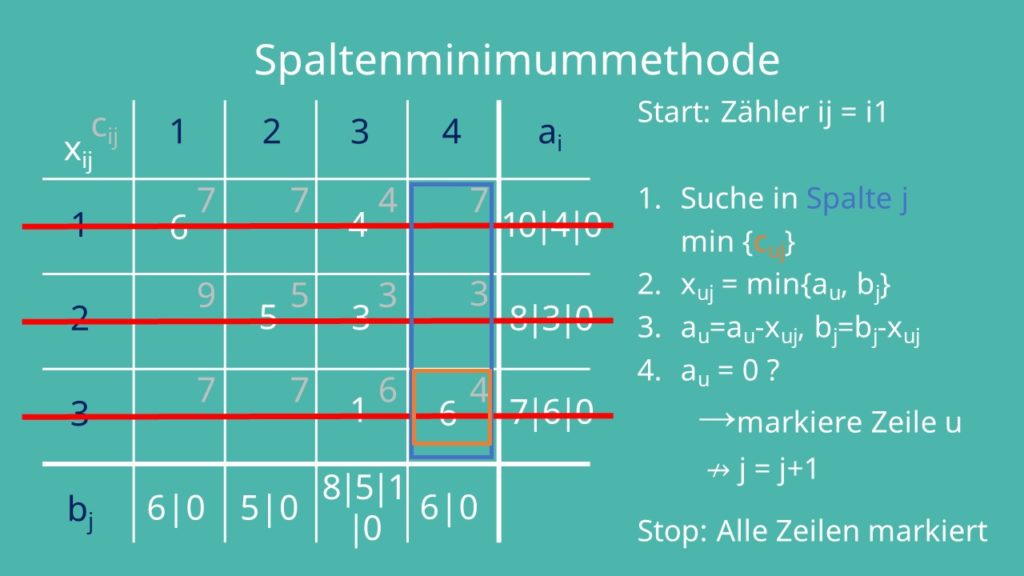
Da unser j nicht erhöht wurde, weil wir Zeile 2 markiert haben, suchen wir in der vierten Iteration in der dritten Spalte nach unserem Minimum. In diesem Fall ist xuj gleich c13 gleich 4.
Die weiteren Iterationen haben wir für dich schon ausgefüllt. Du stoppst das Verfahren, wenn alle Zeilen markiert sind.
Damit hast du deine Basislösung gefunden.
Vogelsche Approximationsmethode
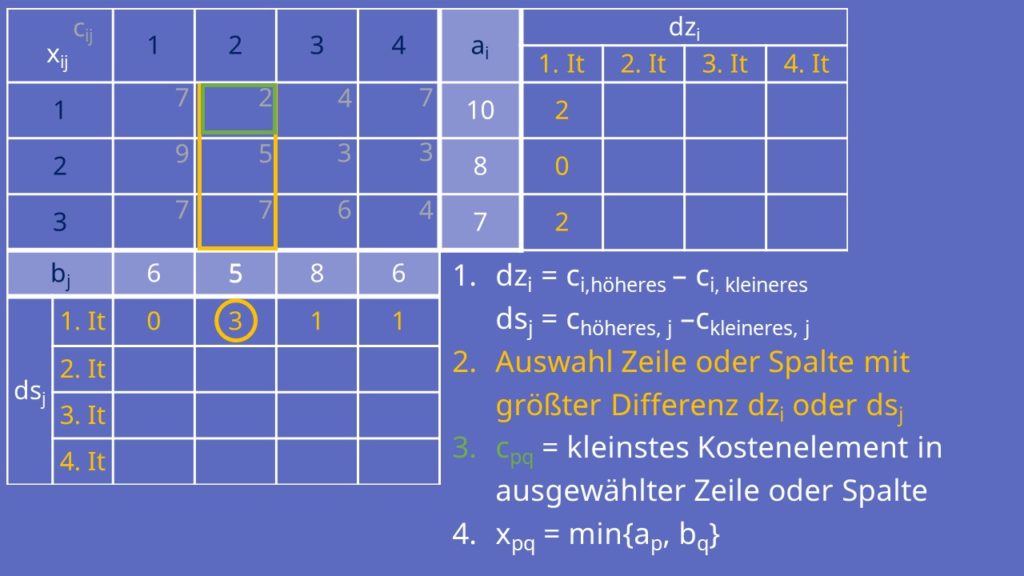
Als drittes gibt es noch die Vogelsche Approximationsmethode. Hierfür brauchst du ein leicht erweitertes Tableau um Differenzzeilen dzi und Differenzspalten dsj. Diese werden nochmal für jede Iteration unterteilt. Da wir bereits wissen, dass wir für dieses Tableau genau vier Iterationen benötigen, haben wir diese schon in 4 Iterationen unterteilt.
Am Anfang sind wieder alle Zeilen und Spalten unmarkiert und alle xij sind gleich 0. Bei der Vogelschen Approximationsmethode errechnest du in der Kostenmatrix für jede unmarkierte Zeile i und Spalte j die Differenz zwischen dem kleinstem und nächsthöherem Wert. Diese Differenz trägst du in dzi beziehungsweise dsj ein.
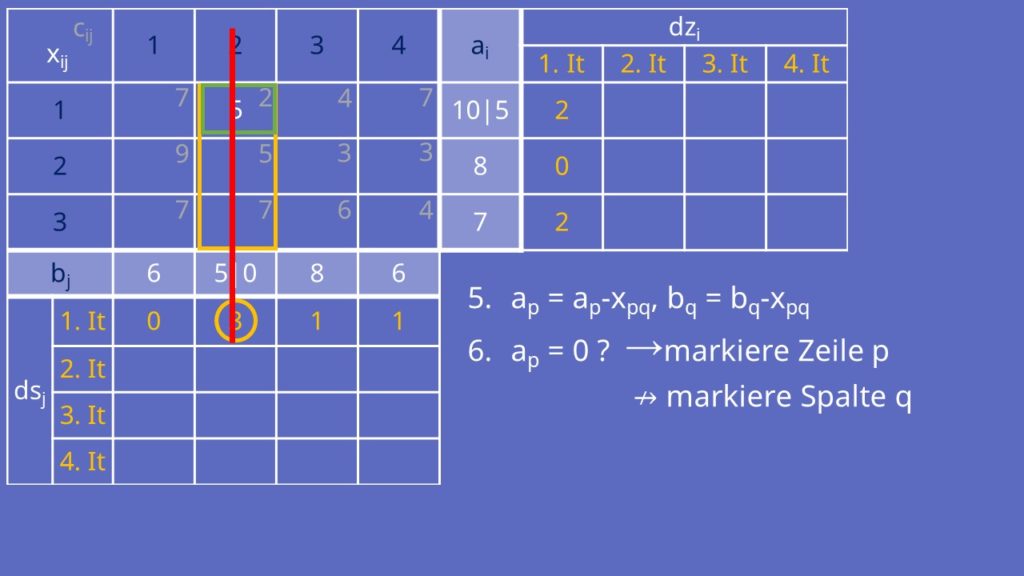
Jetzt suchst du die Spalte oder Zeile mit der höchsten Differenz. Wir wählen Spalte 2 mit der Differenz 3. Nun schaust du welches Kostenelement cpq in der Spalte, beziehungsweise der Zeile, am kleinsten ist. Hier ist das c22 gleich 2. Jetzt setzt du xpq gleich dem Minimum von ap und bq. Hier also x22 gleich dem Minimum von a1 und b2 gleich a1 gleich 5.
Du subtrahierst nun von ap und bq dein xpq. Bei uns ist das für a1 gleich 10 Minus 5 gleich 5 und für b2 gleich 5 Minus 5 gleich 0. Wenn ap gleich 0 ist, markierst du die Zeile p. Ansonsten ist bq gleich Null und du markierst die Spalte q. Bei uns ist a1 nicht 0, weshalb b2 gleich 0 ist und wir die Spalte 2 markieren.
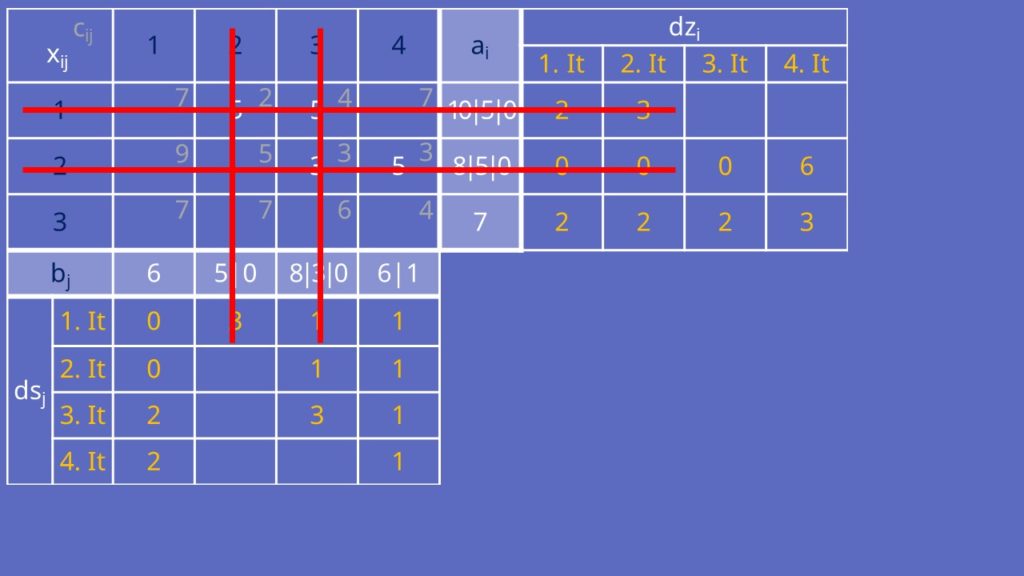
Die nächsten Iterationen füllen wir dir jetzt aus. Sobald alle bis auf eine Spalte oder Zeile markiert sind, musst du nur noch die Restmengen zuteilen, sodass alle ai und bi 0 werden. In unserem Fall musst du dafür nur noch x31 gleich 6 und x34 gleich 1 setzen.
Auch hier haben wir jetzt unsere Basislösung der Vogelschen Approximationsmethode ermittelt.
MODI Methode
Bis jetzt haben wir drei Heuristiken zur Lösung eines Transportproblems kennengelernt. Deren Lösungen waren zwar zulässig, aber noch nicht optimal. Deshalb werden wir jetzt auf eine der bereits vorhandenen Basislösungen die MODI Methode anwenden und daraus die optimale Lösung ermitteln. Wir nehmen für unser Beispiel das Ergebnis der Nordwesteckenregel.
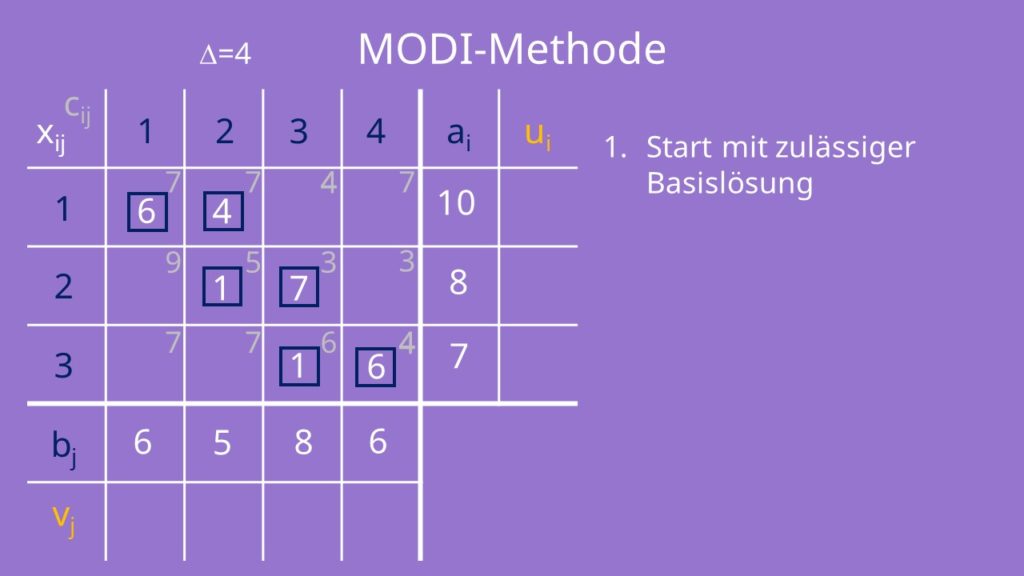
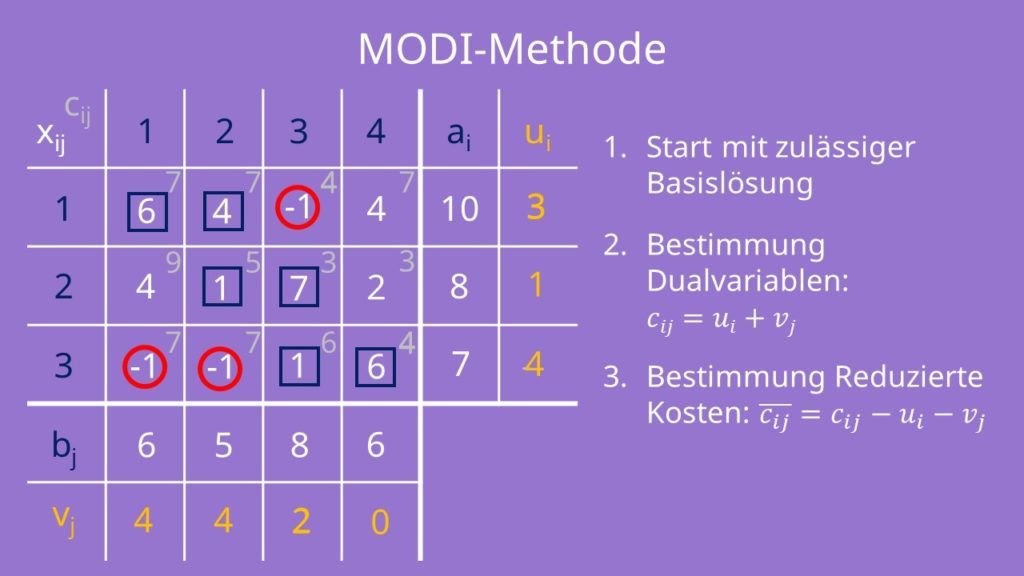
Das Tableau für die MODI Verfahren ist einfach nur um die Dualvariablen der Anbieter ui und Nachfrager vj erweitert. Zusätzlich benötigen wir wieder die Kostenmatrix C in unserem Tableau.
Im ersten Schritt schreibst du die Basislösung aus deinem Heuristikverfahren in das MODI Tableau und markierst sie. Die ai-Spalte und die bj-Zeile bleiben ebenso gleich.
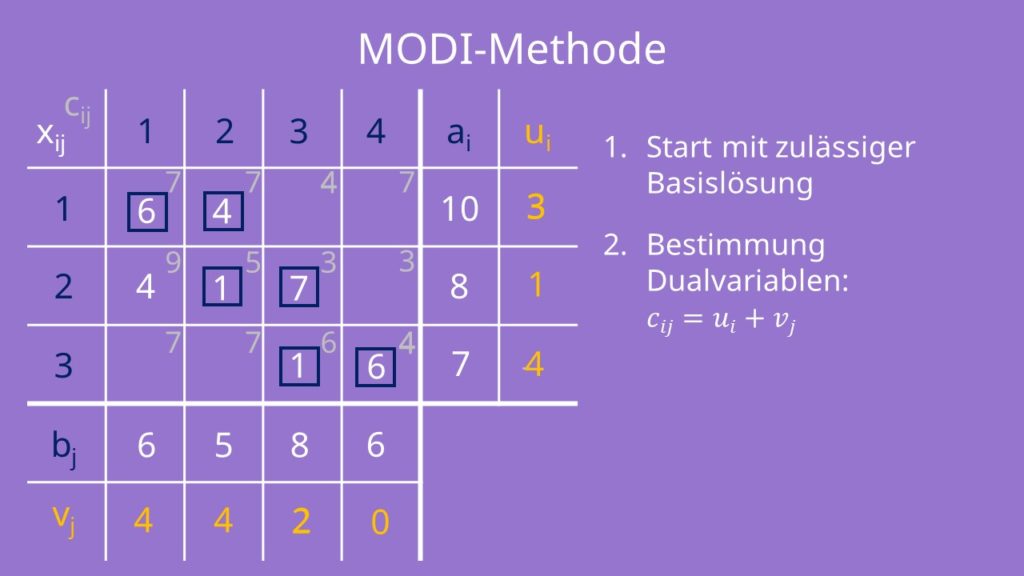
Als zweites bestimmst du die Dualvariablen für die Basisvariablen. Diese setzen sich zusammensetzen aus cij in der Kostenmatrix gleich ui + vj im MODI Tableau. Für eine der Variablen musst du vorerst einen beliebigen Wert annehmen, um alle anderen Wert ermitteln zu können. Wir setzen deshalb zum Beispiel v4 gleich 0. Daraus ergibt sich, dass u3 gleich „4 Minus 0 gleich 4“ sein muss. Und daraus können wir wiederrum folgern, dass v3 gleich 2 sein muss, da „4 plus 2 gleich 6“ ist und so weiter.
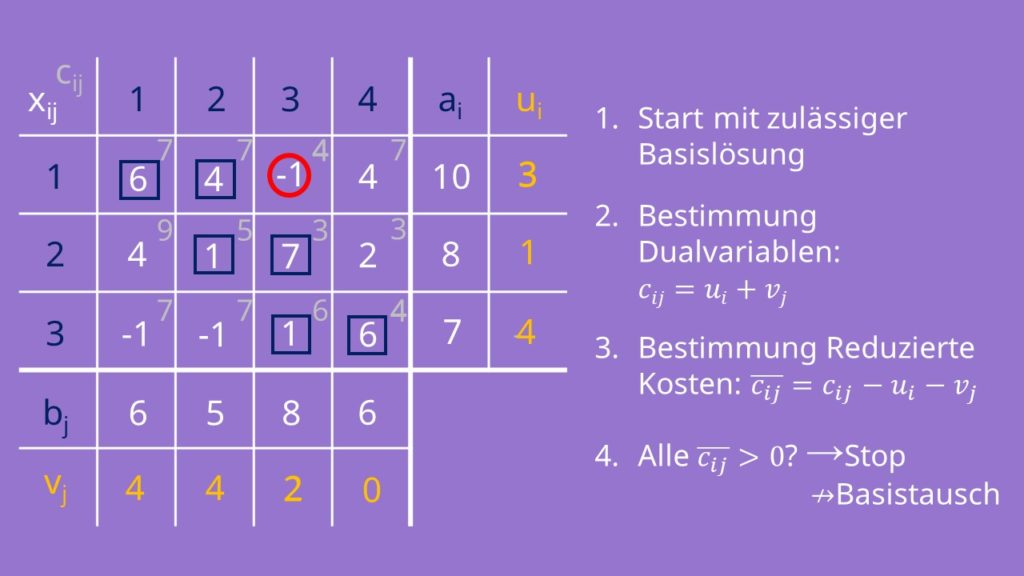
Im dritten Schritt der MODI Methode musst du in den noch freien Felder die reduzierten Kosten für die Nicht-Basisvariablen berechnen. Diese sind ein Maß für den Kostenanstieg des Zielfunktionswertes, wenn xij um eine Mengeneinheit erhöht wird. Die reduzierten Kosten ergeben sich nach der Rechnung: 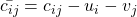 .
. 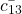 ist also gleich 4-3-2=1. Für die anderen Werte machen wir das genauso. Nachdem du alle reduzierten Kosten berechnet hast, überprüfst du, ob alle
ist also gleich 4-3-2=1. Für die anderen Werte machen wir das genauso. Nachdem du alle reduzierten Kosten berechnet hast, überprüfst du, ob alle 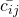 größer gleich Null sind. Ist das der Fall, ist unsere Basislösung optimal und wir stoppen das Verfahren.
größer gleich Null sind. Ist das der Fall, ist unsere Basislösung optimal und wir stoppen das Verfahren.
Ist das aber nicht so – wie in unserem Beispiel – nehmen wir einen Basistausch vor.
Für den Basistausch bei der MODI Verfahren suchst du dir als erstes den negativsten Wert 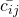 . Hier haben wir drei Werte, die mit „Minus 1“ den gleichen negativen Wert haben. Falls nicht anders vorgegeben, kannst du dir einen der drei aussuchen. Wir wählen
. Hier haben wir drei Werte, die mit „Minus 1“ den gleichen negativen Wert haben. Falls nicht anders vorgegeben, kannst du dir einen der drei aussuchen. Wir wählen 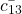 . Dieser wird unsere neue Basisvariable mit dem Wert Delta.
. Dieser wird unsere neue Basisvariable mit dem Wert Delta.
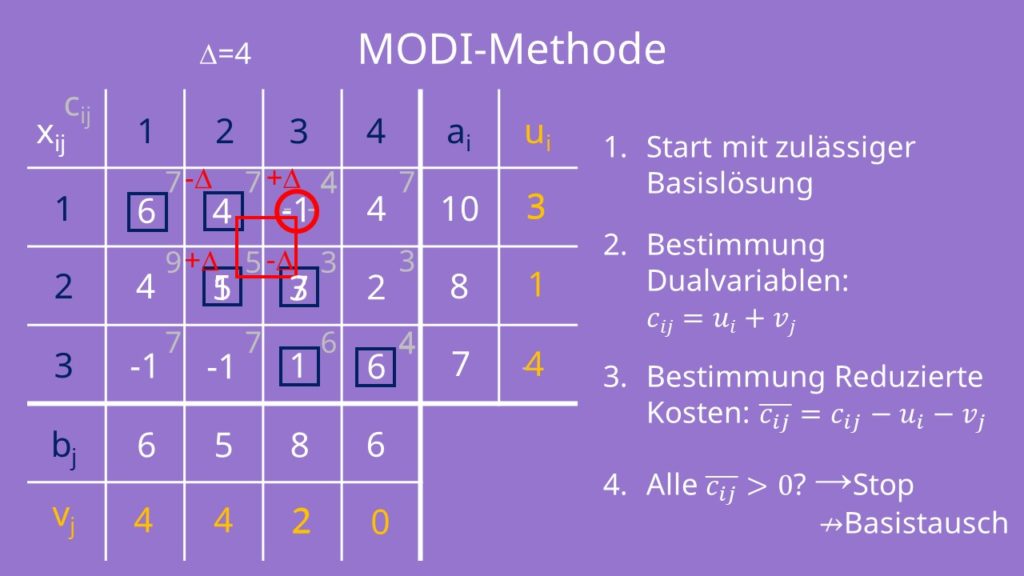
Wir wollen ihn nun erhöhen, da er negative reduzierte Transportkosten, also erhöhte Kosten darstellt. Wir schreiben deshalb ein +Δ an die Zahl. Um diese Erhöhung in der 3. Spalte und der 1. Zeile auszugleichen, schreiben wir für die Basisvariablen darunter und daneben ein „Minus Delta“. Jetzt muss aber auch noch die 2. Zeile ausgeglichen werden. Deshalb markieren wir die Basisvariable mit dem Wert 1 mit einem „Plus Delta“. Wie du siehst, haben wir jetzt einen Ausgleichskreis.
Der Wert von Delta ist der Wert der kleinsten Basisvariable, die mit einem negativen Delta markiert ist. Demnach ist Delta gleich 4. X13 wird also anstelle von x12 unsere neue Basisvariable. Die vier Einheiten werden jetzt nicht mehr von Anbieter 1 nach Nachfrager 2, sondern von 1 nach 3 geliefert. Um die anderen Basisvariablen im Ausgleichskreis anzupassen, addierst beziehungsweise subtrahierst du sie mit Delta, also mit 4. Das ist jetzt unsere neue zulässige Basislösung. Damit haben wir die erste Iteration der MODI Methode geschafft!
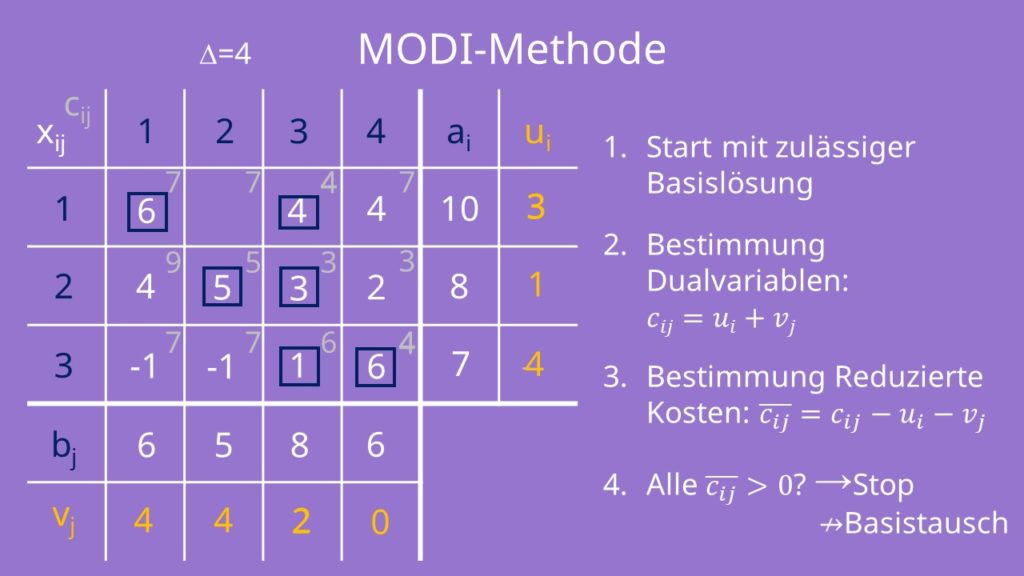
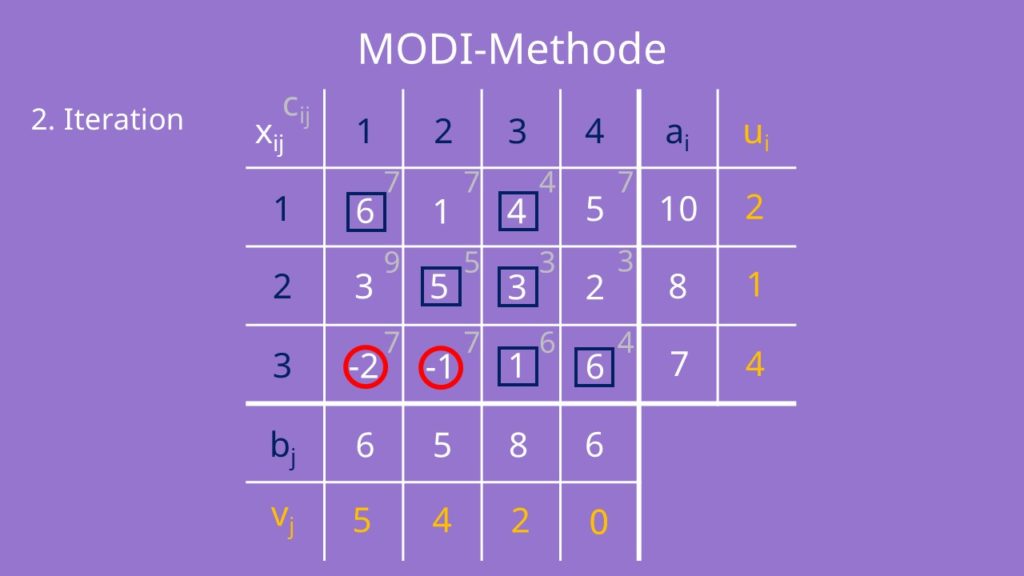
Um zu sehen, ob dein Transportplan jetzt optimal ist, musst du die zweite Iteration beginnen und die Dualvariablen und die reduzierten Kosten neu bestimmen. Wie du siehst, haben wir hier immer noch negative reduzierte Kosten und damit noch keine optimale Lösung.
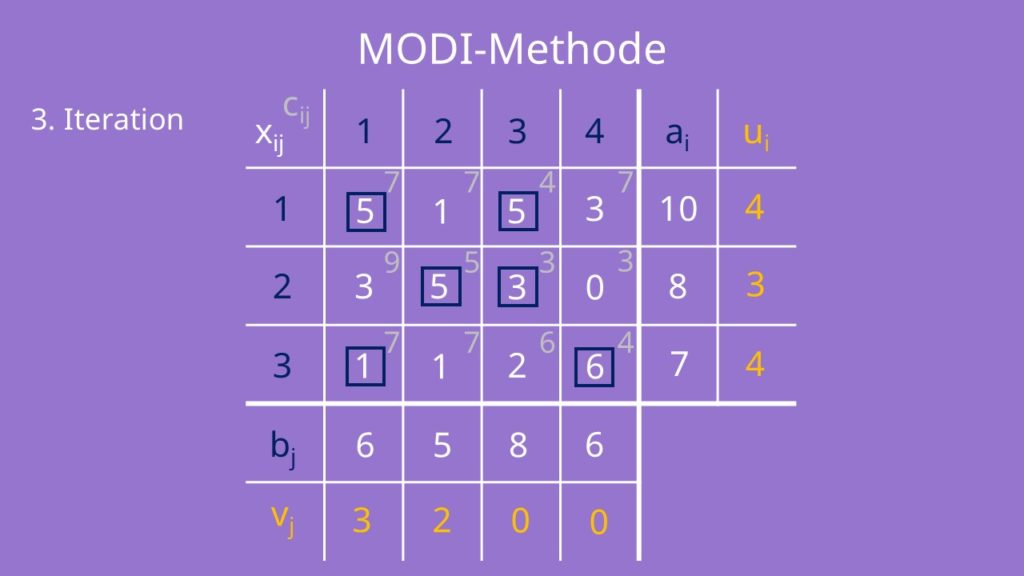
Wenn wir jetzt die dritte Iteration durchführen, siehst du, dass wir keine negativen reduzierten Kosten mehr haben. Wir können das MODI Verfahren damit abbrechen und haben unsere optimale Lösung bestimmt.
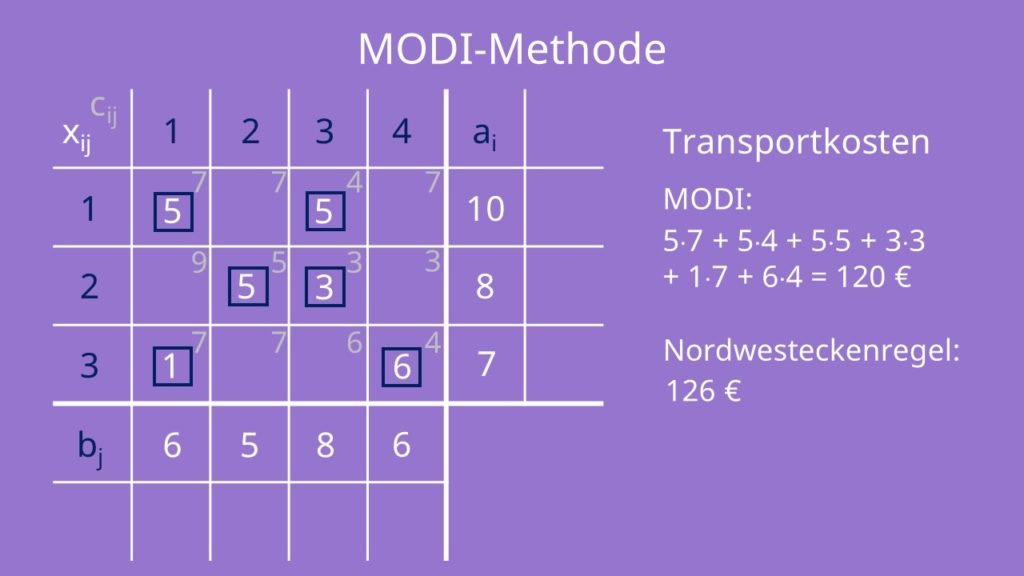
Wenn du nun die Zielfunktion des Transportproblems mit der MODI Methode berechnen möchtest, musst du nur die Basisvariablen, also die Transportmenge des Guts, mit ihren jeweiligen Kosten multiplizieren. Damit kommen wir auf Transportkosten von 120€. Der Zielfunktionswert der Basislösung, die wir mit der Nordwesteckenregel im vorherigen Video erhalten haben, ist 126 €.
Du siehst: Durch die MODI Methode konnten wir die Kosten des Transportproblems optimieren.