Ziehen mit Zurücklegen mit Reihenfolge

Du möchtest wissen, welche Formel du bei Ziehungen mit Zurücklegen unter Beachtung der Reihenfolge verwenden musst? Dann wird dir dieser Beitrag weiterhelfen!

Wir bringen Ordnung in das Kugelchaos und erklären dir in unseren Videos alles, was du zu den Urnenmodellen „Ziehen mit Zurücklegen“ und „Ziehen ohne Zurücklegen“ wissen solltest.

Variation mit Wiederholung

Ein anschauliches Beispiel hierfür sind die Kombinationen eines Fahrradschlosses. Die Reihenfolge der Zahlen machen einen Unterschied, allerdings kann jede Zahl beliebig oft vorkommen- es handelt sich also um ein Zufallsexperiment mit Zurücklegen. Gehen wir davon aus, du hast die 5-stellige Kombination deines Fahrradschlosses vergessen. Jede Zahl könnte eine Ziffer zwischen 1 und 6 sein. Wie viele Möglichkeiten kannst du ausprobieren?

Wahrscheinlichkeit Ziehen mit Zurücklegen mit Reihenfolge

Für jede der 5 Stellen der Kombination gibt es 6 Möglichkeiten. Insgesamt gibt es also 6 hoch 5 gleich 7.776 mögliche Kombinationen für das Zahlenschloss.

Allgemein lautet die Formel wie folgt:

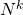
Groß N steht dabei wieder für die Anzahl an Elementen, aus denen gezogen wird, in unserem Fall also die 6 möglichen Ziffern, und klein k steht für die Anzahl der Ziehungen, die in diesem Fall den 5 Stellen der Kombination entsprechen.