Messgenauigkeit
Im ersten Artikel hast du schon einen kleinen Einblick in die Welt der Messtechnik erhalten. Jetzt beschäftigen wir uns noch intensiver mit Messgenauigkeiten.
Als erstes benötigen wir eine allgemeine Definition, mit der wir arbeiten können. Messgenauigkeit ist der Unterschied zwischen dem gemessenen Wert und dem realen Wert. Das bedeutet: Die Abweichung F ist der angezeigte Wert minus der richtige Wert.
Inhaltsübersicht
Abweichung
Die Abweichung hängt mit der Empfindlichkeit des Messgeräts zusammen. Die Empfindlichkeit ist unter DIN 1319 definiert als: „Änderung des Wertes der Ausgangsgröße eines Messgerätes bezogen auf die sie verursachende Änderung des Wertes der Eingangsgröße“. Sie lässt sich berechnen mit:
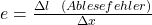
Dabei ist Delta L der Ablesefehler und Delta x aus der Delta L resultierenden Abweichung des Messwertes x. Für die relative Abweichung gilt:
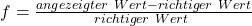
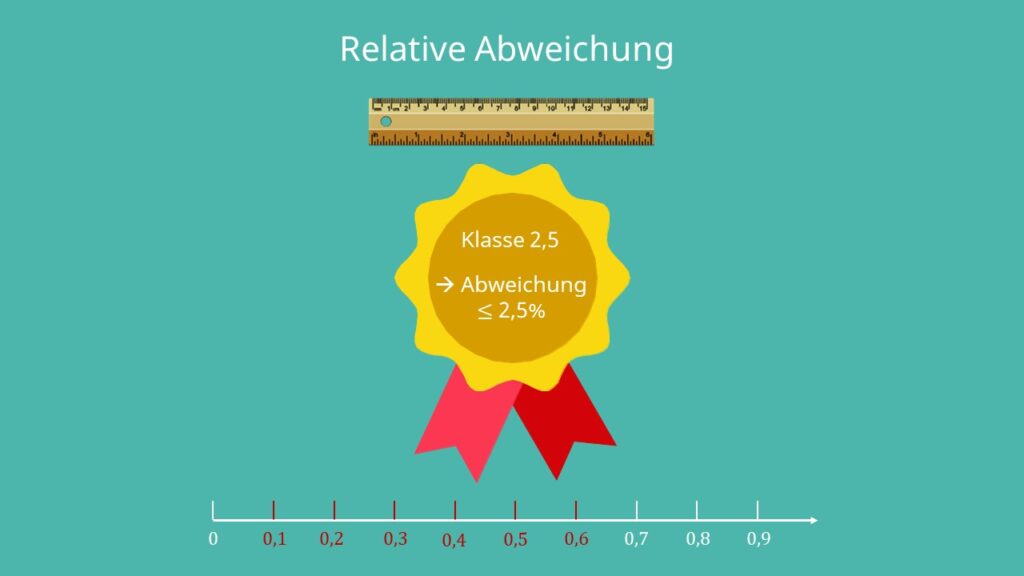
Sie gibt die Klasse eines Messgeräts an. Die Klasse 2,5 beispielsweise bedeutet, dass das Messgerät garantiert eine Abweichung kleiner oder gleich 2,5% hat. Je nachdem wie genau der Versuch sein muss, wird die jeweilige Klasse ausgesucht. Muss das Ergebnis sehr genau sein, wird eine Klasse zwischen 0,1 bis 0,6 gewählt. Du fragst dich jetzt bestimmt, welche Klasse du verwenden sollst.
Durch die Unterteilung der Abweichung in Systematische und Zufällige Abweichung ist es leichter bei verschiedenen Versuchen die richtige Klasse auszuwählen.
Systematische Abweichung
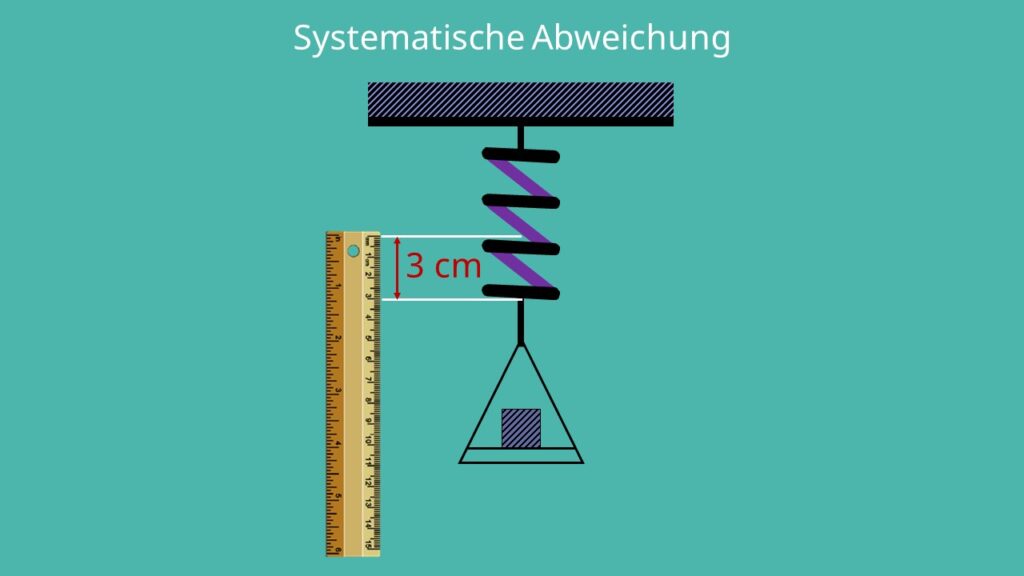
Um Systematische Abweichungen zu verstehen, stellen wir uns jetzt einen Versuch vor. Wir wollen eine Messung durchführen, die du nicht nur einmal, sondern mehrmals unter gleichen Bedingungen wiederholst. Führst du diesen Versuch durch und findest die Abweichung heraus, dann kannst du davon ausgehen, dass du dasselbe Ergebnis erhältst, wenn du ihn unter den gleichen Bedingungen nochmals ausführst. Denn Systematische Abweichungen treten immer an einer bestimmten Stelle auf und mit der gleichen Abweichung.
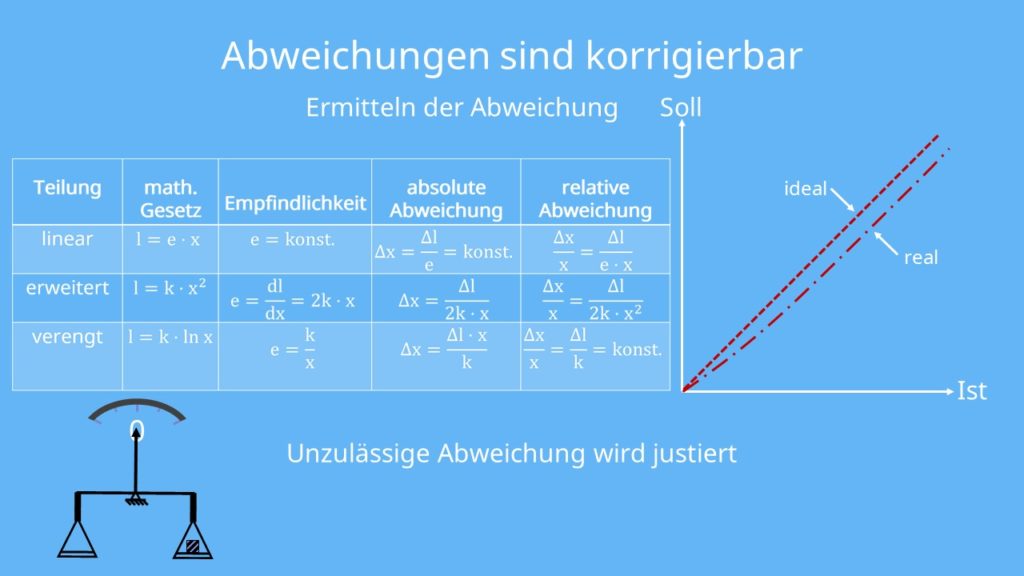
Abweichungen sind aber korrigierbar. Man unterscheidet dabei zwischen drei Fällen:
Betrachten wir jetzt den linearen Fall und korrigieren ihn. Das geschieht beispielsweise durch Kalibrierung. Darunter versteht man das Ermitteln der Abweichung, sodass der Fehler korrigiert werden kann. Man benötigt dafür den angezeigten und den richtigen Wert und erhält durch die Kalibrierung ein Kalibrierdiagramm.
Anhand des Diagramms können wir erkennen, wie der ideale Wert sein sollte und wie der reale Wert ist. Falls eine Abweichung unzulässig ist, muss justiert werden. Das bedeutet, dass das Messgerät so eingestellt wird, dass beim Kalibierdiagramm beide Linien gleich sind.
Methodische Abweichungen
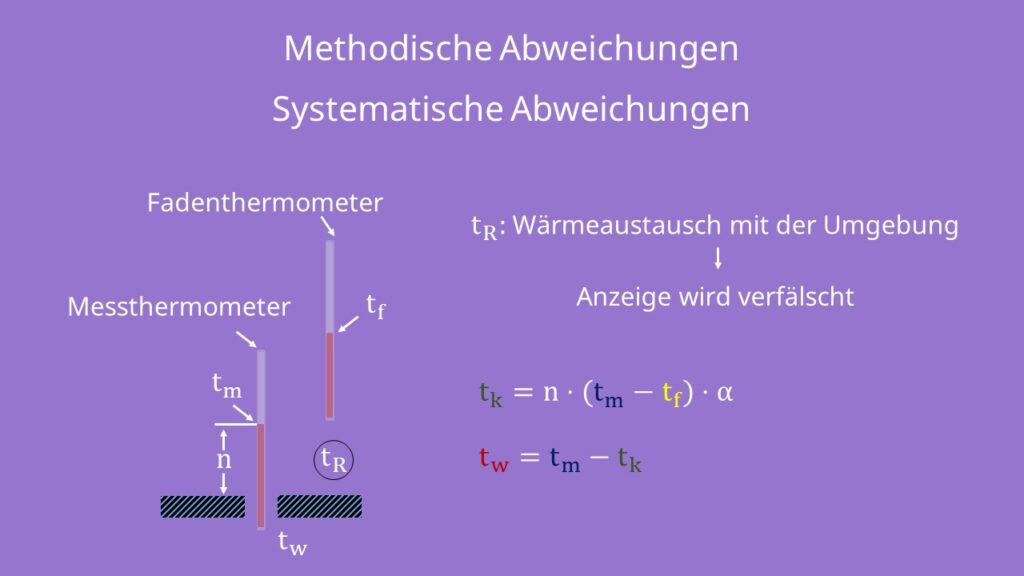
Zu den Systematischen Abweichungen zählen auch Methodische Abweichungen. Schauen wir uns als Beispiel ein Thermometer an. Führst du es vollständig in einen Raum ein, so kommt es zu keinen Abweichungen. Ist es aber unvollständig im Raum, dann kommt es zum Wärmeaustausch mit der Umgebung tR. Dadurch wird die Anzeige verfälscht. Methodische Abweichungen sind also von der Umgebung abhängig. Diese lassen sich zwar nicht immer korrigieren, wir werden es nun aber versuchen.
Du möchtest messen wie groß tw ist. Da die Temperatur tm niedriger ist als t w, benötigen wir ein zusätzliches Hilfsmittel: Das Fadenthermometer. Mit diesem kannst du einen Korrekturwert tk bestimmen. Damit lässt sich dann tw berechnen:
Zufällige Abweichungen
Kommen wir jetzt zu den zufälligen Abweichungen. Diese sind so zufällig, dass niemand im Voraus sagen kann, wo sie auftreten werden. Denn sie können an jeder Stelle vorkommen und müssen nicht immer die gleiche Messabweichung haben. Eine solche Abweichung kann natürlich auch nur ein Ablesefehler des Beobachters sein.
Wie du bereits gelernt hast, spielt hier auch die Empfindlichkeit eine Rolle. Stellt man die Formel nach Delta x um, erhält man die absolute Abweichung.
Die relative Abweichung wäre in diesem Fall:
Wir möchten die relative Abweichung so gering wie möglich halten. Wenn wir die Formel betrachten, müsste gelten:
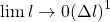 =0
=0
und
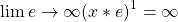
Somit geht die relative Abweichung gegen Null.
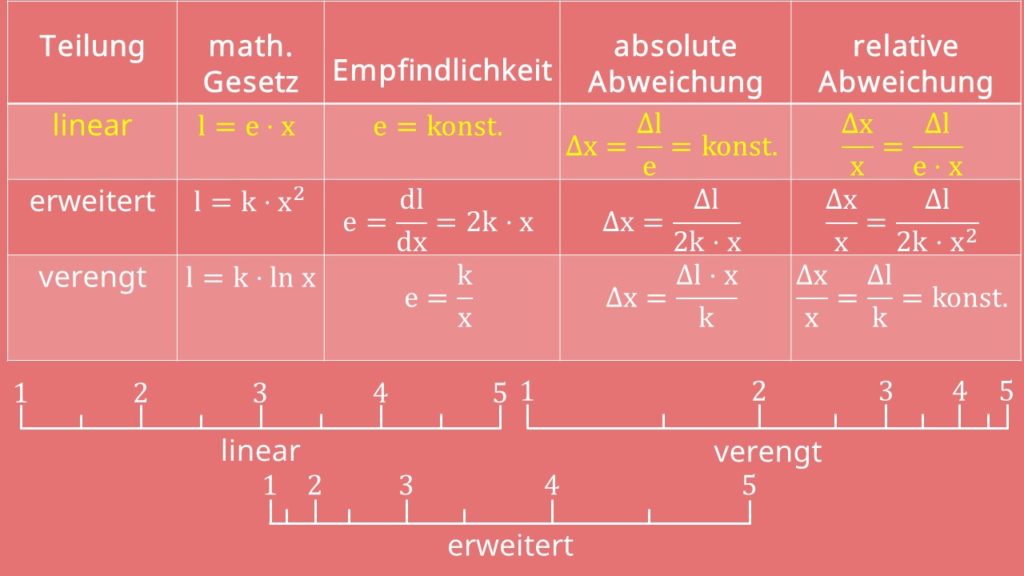
Wir haben bisher nur den linearen Fall betrachtet. Je nach Fall musst du die passende Formel und die zugehörige Skala verwenden.