Hebelgesetz Phasendiagramm
Mit den Hebelgesetzen kann bei einem Phasendiagramm, das aus zwei Komponenten besteht, die Konzentration und die relativen Anteile der Bindungspartner in verschiedenen Phasen berechnet werden. Wir zeigen dir mit unserem Video in unter 5 Minuten wie das geht.
Inhaltsübersicht
Hebelgesetz Werkstoffkunde
Das Hebelgesetz in der Werkstoffkunde kommt aus der Thermodynamik. Es dient zur Analyse von verschiedenen Phasen eines, aus zwei Komponenten bestehenden, Phasendiagramms . Mit der Hilfe der Formeln kann dann die Konzentration der zwei Bindungspartner in einer Mischphase berechnet werden. Die Konzentration ist allerdings immer abhängig von den Anteilen der Atomsorten in den Phasen.
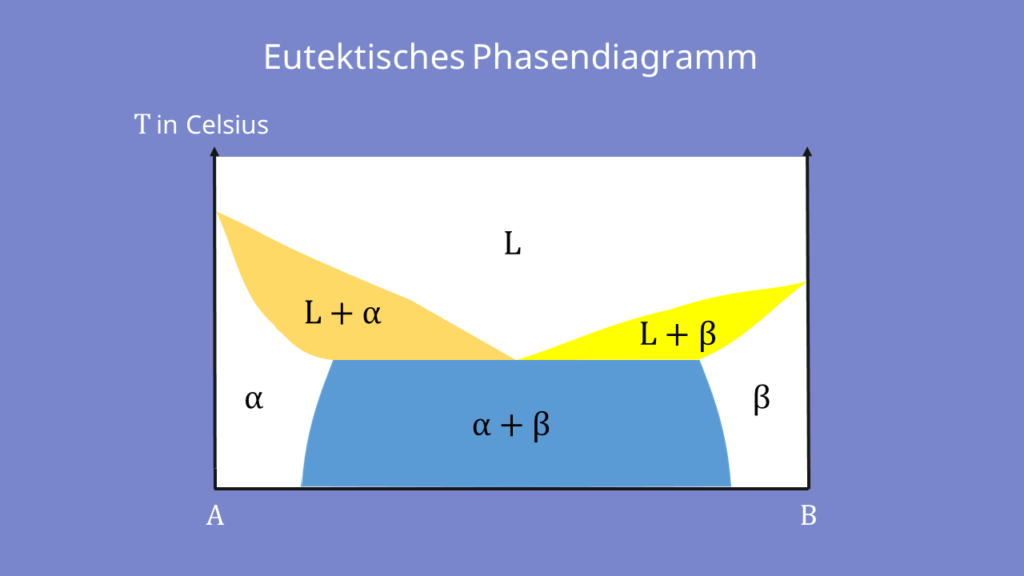
Die Hebelgesetze in der Werkstoffkunde kann man durch Überlegungen am eutektischen Diagramm herleiten. Das Phasendiagramm kann wie folgt aussehen:
In diesem Phasendiagramm sind die unterschiedlichen Zustände Alpha α, Beta β, die flüssige L-Phase und die jeweiligen Mischphasen eingetragen. Die Phasen sind durch eine bestimmte Zusammensetzung der zwei Bindungspartner klar definiert.
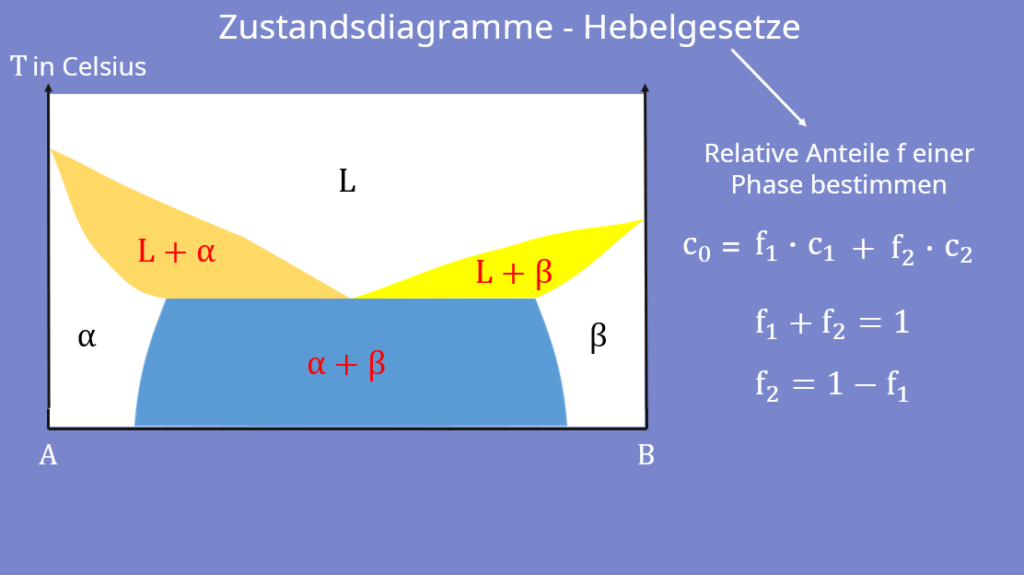
Doch wie sieht das bei den Mischphasen aus? Dafür überlegen wir uns, wie sich die Gesamtkonzentration c0 in einer Mischphase an einer bestimmten Stelle zusammensetzt. Es gibt zum einen die Konzentration der Phase eins c1 und zum anderen die Konzentration der Phase zwei c2. Doch Vorsicht, wir können diese nicht einfach addieren! Bevor wir das machen, müssen wir sie noch mit den jeweiligen relativen Anteilen f der beiden Phasen multiplizieren. Damit erhalten wir dann die Gesamtkonzentration c0:
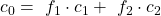
Die Anteile der beiden Phasen sind dabei per Definition in Summe gleich eins:
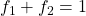
Hebelgesetz Werkstoffkunde Formel
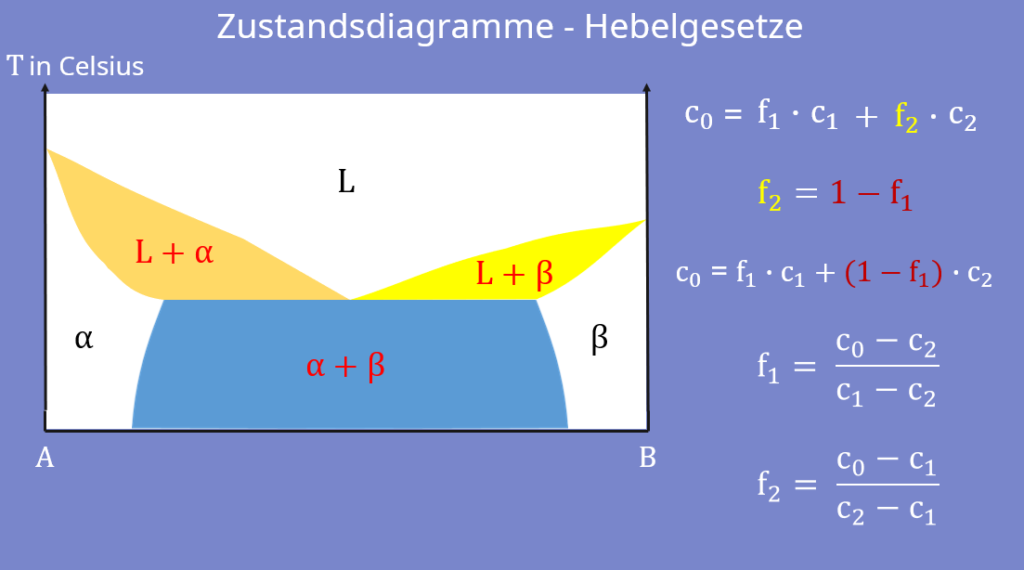
Mit diesem Wissen können wir uns jetzt auch schon die Hebelgesetze für das Phasendiagramm herleiten. Dabei geht es darum, die relativen Anteile f einer Phase zu bestimmen. Wir wollen die Gleichung der Hebelgesetze also nach einem f umstellen.
Durch
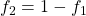
kann der relative Anteil f2 eliminiert werden. Jetzt wird die komplette Berechnung nach f1 umgestellt. So ergibt sich das erste Hebelgesetz:
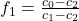
Analog dazu können wir für f2 vorgehen und erhalten:
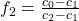
Um die Hebelgesetz Formeln für einen konkreten Fall anzupassen, ersetzen wir einfach die Indizes mit den gewünschten Phasen. Für die Alpha-Beta-Phase unseres Diagramms ergibt sich beispielsweise:
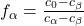
Hebelgesetz Aufgaben
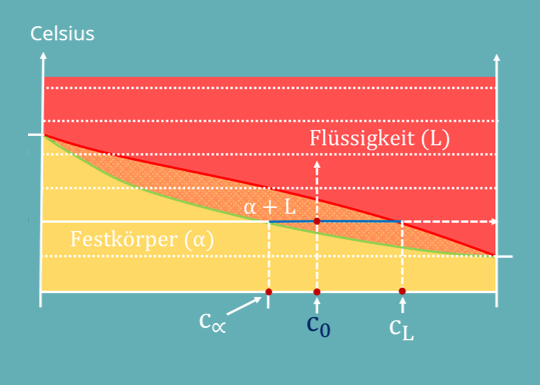
Für das Beispiel nehmen wir das Zustandsdiagramm von Kupfer und Nickel mit einer L- und einer Alpha Phase. Wir wollen mit den Hebelgesetzen herausfinden, wie die Anteile der beiden Phasen bei einer Konzentration von 60 Prozent Kupfer und 1.200 Grad Celsius sind.
Zuerst kannst du im Phasendiagramm das 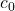 , das 60 Prozent Kupfer beträgt, auf der x-Achse ablesen. Das ist die zusammengesetzte Konzentration der beiden Phasen. Jetzt gehen wir von
, das 60 Prozent Kupfer beträgt, auf der x-Achse ablesen. Das ist die zusammengesetzte Konzentration der beiden Phasen. Jetzt gehen wir von 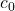 aus senkrecht nach oben, bis wir die gewünschte Temperatur von 1200 Grad Celsius erreicht haben.
aus senkrecht nach oben, bis wir die gewünschte Temperatur von 1200 Grad Celsius erreicht haben.
Hier zeichnen wir eine Orthogonale, bis wir auf der eine Seite die Solidus– und auf der anderen die Liquiduslinie berühren.
Um zu verstehen, warum man das nun als Hebelgesetz für Phasendiagramme bezeichnet, musst du die beiden Anteile ins Verhältnis setzen:
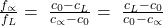
Im Diagramm erkennst du den Zähler links und den Nenner rechts von der Gesamtkonzentration. Das sind unsere beiden Hebel. An den Enden der beiden Hebel kannst du die Konzentrationen der beiden Phasen ablesen.
Ein genaues Ergebnis ist bei gezeichneten Diagrammen oft schwierig abzulesen. Das ist allerdings nicht so schlimm. Denn um das Gesetz zu verstehen, reicht uns eine Annäherung. Auf der linken Seite können wir die Konzentration der Phase Alpha bei ungefähr 50 Prozent ablesen, rechts liegt die L-Phase bei ungefähr 77 Prozent. Setzen wir das in unsere Formel für die Anteile ein, erhalten wir:
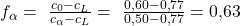
und:
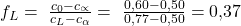
Der Anteil an der Alpha-Phase ist deutlich höher. Eigentlich auch logisch, oder? Wir befinden uns im Diagramm ja auch viel näher an der Alpha-Phase. Zur Kontrolle addieren wir noch die beiden Anteile und erhalten:
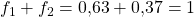
Super! Jetzt kannst du die Anteile der Mischphasen in allen Zustandsdiagrammen bestimmen.