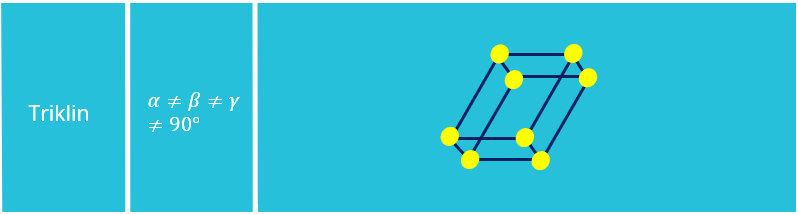
Bravais Gitter
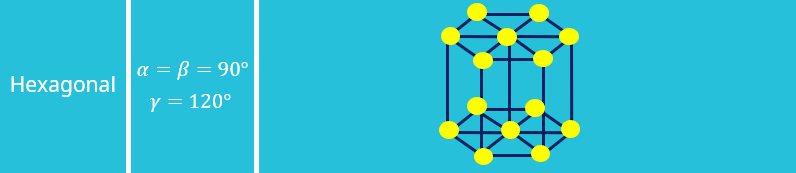
Die 14 Bravais Gitter ergeben sich über die sogenannten Elementarzellen. Diese Zellen lassen sich in sieben Kristallsysteme, die oftmals weitere Unterarten haben, einteilen. Es gibt das kubische, tetragonale, rhombische, hexagonale, trigonale, monokline und trikline System für Kristallgitter. Wie diese zustande kommen und wie sie genau aussehen, erklären wir dir in unserem Video .
Inhaltsübersicht
Kristallgitter
Um auf die Bravais Gitter zu schließen, müssen in einem ersten Schritt die Bestandteile einer Kristallstruktur erklärt werden. Ein Kristall besteht immer aus einem Gitter und einer dazugehörigen Basis. In diesem Fall wird unter einem Gitter eine regelmäßige dreidimensionale Anordnung von Atomen verstanden. Die Basis hingegen ist eine periodisch wiederkehrende Struktureinheit in einem Gitter und kann aus einzelnen oder mehreren Atomen bestehen. Zusammen bilden sie das Kristallgitter oder auch die Kristallstruktur.
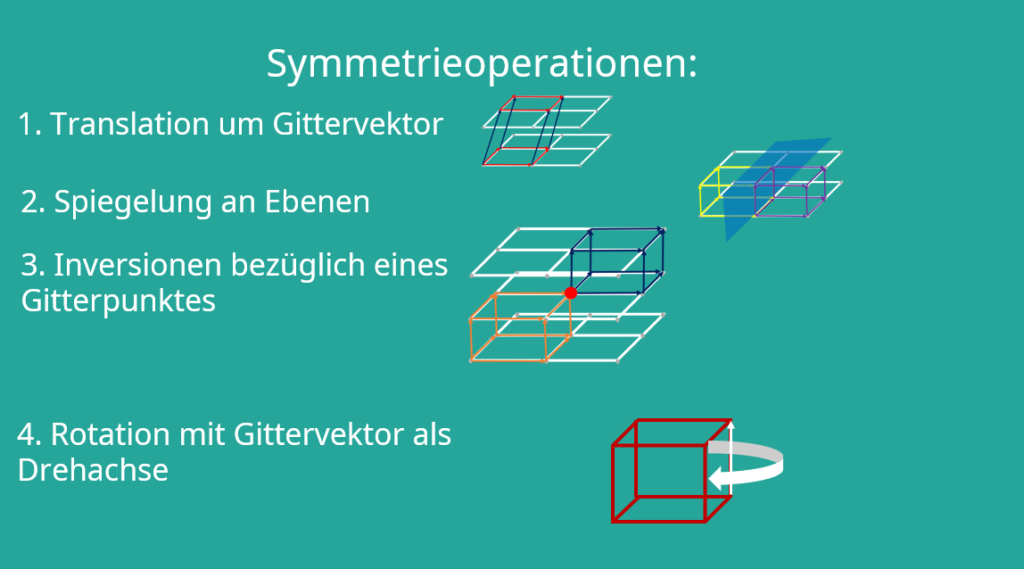
Anhand von vier verschiedenen Symmetrieoperationen können Kristallgitter in unterschiedliche Gruppen unterteilt werden. Je nachdem welche Symmetrie der Kristall hat, kann er eingeordnet werden.
- Die Translation um einen beliebigen Gittervektor
- Die Spiegelung an Ebenen
- Die Inversion bezüglich eines Gitterpunktes
- Die Rotation um einen Gittervektor
Elementarzelle
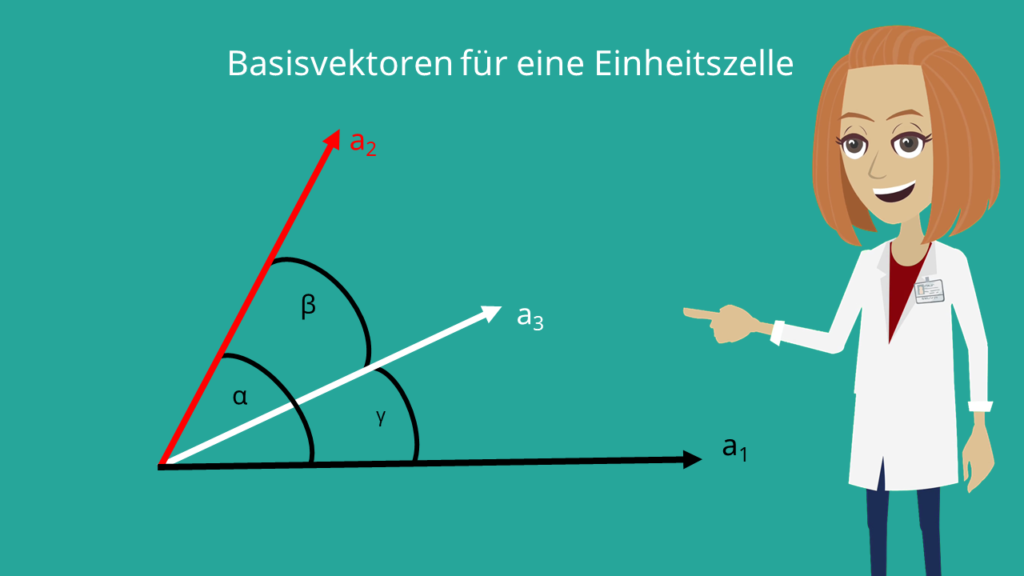
Des Weiteren hat jedes dreidimensionale Kristallgitter drei elementare Translationsvektoren, die sich auch Basisvektoren nennen. Die Vektoren a1, a2 und a3 spannen, je nach Winkel 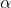 ,
, 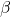 und
und 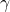 zwischen ihnen, ein unterschiedliches Parallelepiped (Spat) auf. Durch eine Aneinanderreihung von diesem entsteht dann der Kristall. Genau dieses Parallelepiped wird auch als Einheitszelle oder Elementarzelle eines Kristallgitters bezeichnet. Mit so einer Zelle kann wiederum jedes Gitter beschrieben werden. Außerdem wird die Elementarzelle mit dem kleinsten Volumen in einer kristallinen Struktur primitive Einheitszelle genannt.
zwischen ihnen, ein unterschiedliches Parallelepiped (Spat) auf. Durch eine Aneinanderreihung von diesem entsteht dann der Kristall. Genau dieses Parallelepiped wird auch als Einheitszelle oder Elementarzelle eines Kristallgitters bezeichnet. Mit so einer Zelle kann wiederum jedes Gitter beschrieben werden. Außerdem wird die Elementarzelle mit dem kleinsten Volumen in einer kristallinen Struktur primitive Einheitszelle genannt.
Die 14 Bravais Gitter
Eine Elementarzelle wird durch drei Translationsvektoren aufgespannt. Jene können sich von Kristall zu Kristall in Länge und Winkel zueinander unterscheiden. Der Physiker Auguste Bravais hat diese Unterschiedlichkeiten in Kristallsysteme eingeteilt und sie Bravais Gitter genannt. So gibt es nach ihm 14 Gitter, bei denen es sich aber nicht um primitive Elementarzellen handeln muss.
Kubisches Kristallsystem
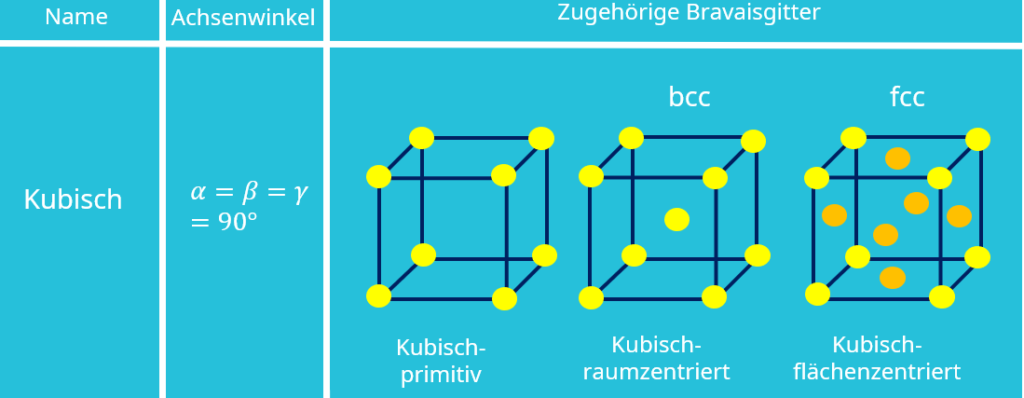
Das kubische Bravais Gitter hat die höchste Symmetrie und lässt sich in kubisch-primitiv, kubisch-raumzentriert und kubisch-flächenzentriert unterteilen. Das Kristallgitter kubisch-raumzentriert wird auch als bcc für body centered cubic und das kubisch-flächenzentrierte Gitter auch als fcc für face centered cubic bezeichnet. Anzumerken ist noch, dass hier alle drei Basisvektoren gleich lang sind, also 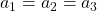 gilt und alle Winkel 90° entsprechen.
gilt und alle Winkel 90° entsprechen.
Wichtig ist, dass sich bei einem raumzentrierten Kristallgitter genau ein Atom in der Mitte der Elementarzelle befindet. Das flächenzentrierte Kristallsystem hingegen kennzeichnet sich durch ein Teilchen auf jeder Seitenfläche des Würfels.
Orthorhombisches Kristallsystem
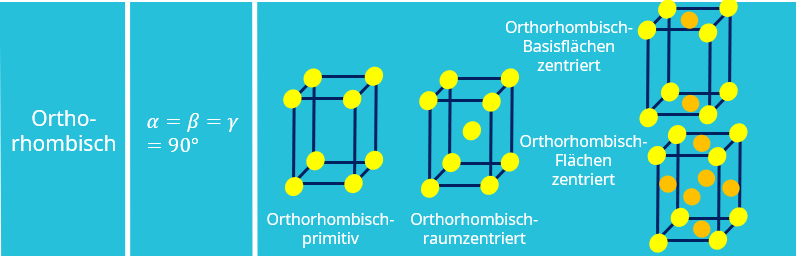
Das nächste Bravais Gitter ist ein Rechteck mit unterschiedlichen Seitenlängen (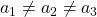 ) und drei identischen Winkeln von 90° (
) und drei identischen Winkeln von 90° (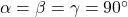 ). Bei diesem Kristallgitter gibt es ein orthorhombisch-primitives, ein orthorhombisch-raumzentriertes, ein orthorhombisch-basisflächenzentriertes und ein orthorhombisch-flächenzentriertes System.
). Bei diesem Kristallgitter gibt es ein orthorhombisch-primitives, ein orthorhombisch-raumzentriertes, ein orthorhombisch-basisflächenzentriertes und ein orthorhombisch-flächenzentriertes System.
FCC Gitter und Elementarzelle
Wichtig ist bei der Unterteilung, dass nicht alle dargestellten Gitter immer primitive Einheitszellen sind. Das heißt, dass innerhalb eines Bravais Gitters noch Zellen mit weniger Volumen gefunden werden können. Zum Beispiel tritt dies bei der Fcc-Kristallstruktur auf. Dennoch wird das kubisch-flächenzentrierte System bevorzugt, da hier die einfache kubische Symmetrie besser erkennbar ist.
Es gibt noch mehr Gittersysteme. Jedoch sind die 14 genannten Kristallgitter, diejenigen die als Bravais Gitter bezeichnet werden.
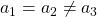 ) verschieden. Alle Winkel betragen wiederum 90°.
) verschieden. Alle Winkel betragen wiederum 90°.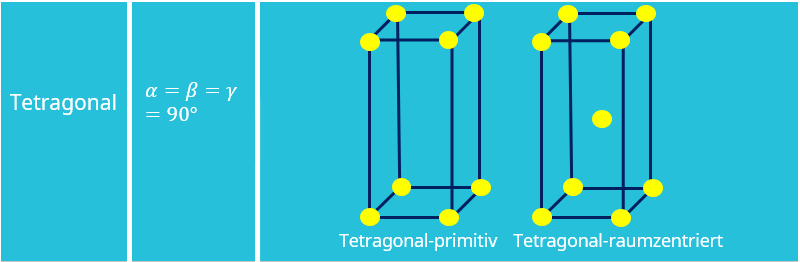
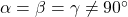 ).
).
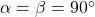 und
und 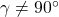 aus.
aus.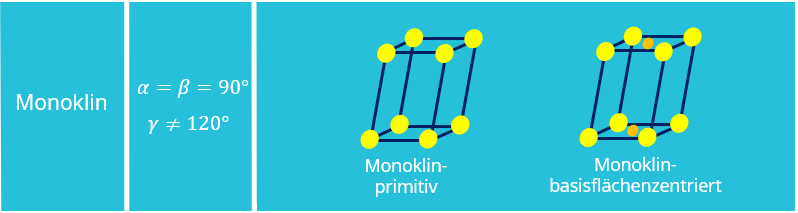
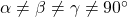 .
.