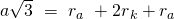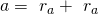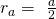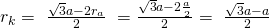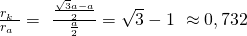Radienquotientenregel
Mit Hilfe der Radienquotientenregel kann man ganz einfach die Kristallstruktur ermitteln, die aus der Verbindung zweier Atome mit unterschiedlichen Ionenradien entsteht. Wichtige Begriffe sind hier die Atomgröße (normalerweise der Atomradius) und die Gitterstruktur. Auch von der Koordinationszahl solltest du was gehört haben. Sagt dir nichts? Dann bist du bei uns richtig!
Inhaltsübersicht
Koordinationszahl, Radienquotientenregel und Strukturtypen- anhand der NaCl Struktur veranschaulicht
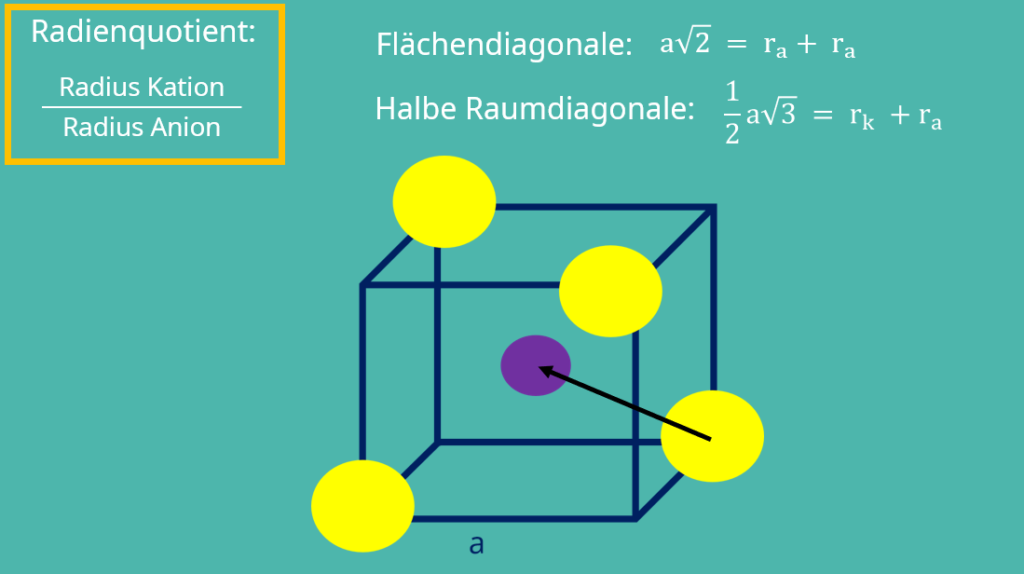
Hier einmal der Zusammenhang zwischen Atomgröße und Gitterstruktur: Um die Atomgröße zu beschreiben, verwendet man normalerweise den Radius. Wie du dir bestimmt schon denken kannst, hat dieser auch etwas mit der Radienquotientenregel zu tun. Der Radienquotient wird berechnet mit:
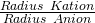
Diese einfache Formel hilft dir zu bestimmen, in welchem Strukturtyp ein Salz kristallisiert. Doch wie genau funktioniert das?
Beispielrechnung bei tetraedischer Anordnung
Betrachten wir zunächst eine tetraedrische Anordnung. Diese legen wir auf das kubische Gitter mit den Anionen in vier Ecken und dem Kation in der Mitte.
Zur Vereinfachung werden wir im Folgenden den größeren Radius des Anions mit und den kleineren des Kations mit bezeichnen. Wir haben also zwei Unbekannte, die wir ins Verhältnis setzen wollen. Das Ziel ist es, einen generellen Zusammenhang herzuleiten. Wir rechnen daher ohne Zahlenwerte. Gegeben ist weiterhin die Seitenlänge a, die wir in unserer Betrachtung eliminieren wollen, da sie unbekannt ist. Dies gelingt über das Erstellen zweier Gleichungen. Die erste erhalten wir über die Flächendiagonale:
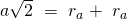
Jedes Anion liegt zur Hälfte im Würfel, sein Radius liegt also genau zwei Mal auf der Flächendiagonalen.
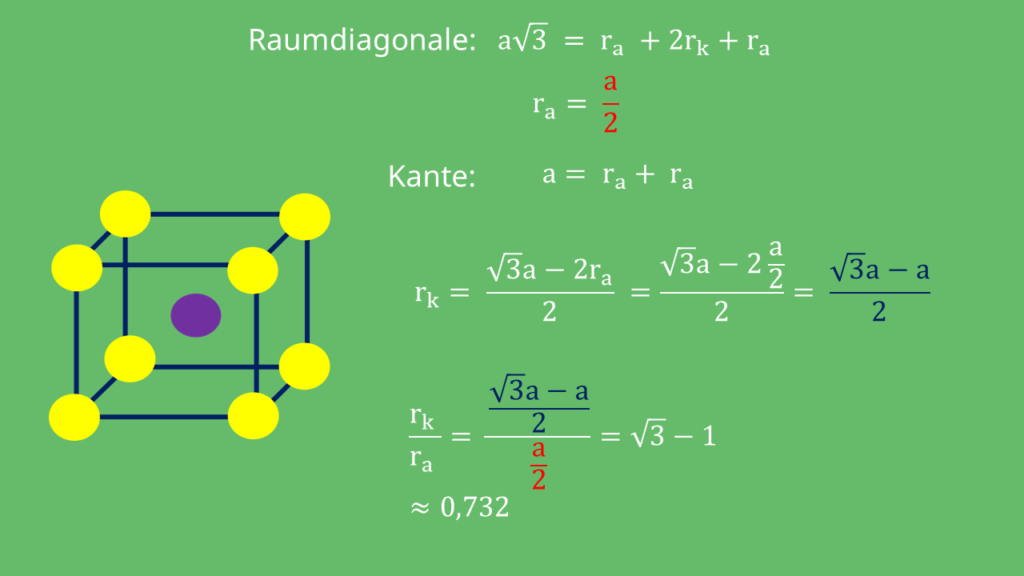
Für die halbe Raumdiagonale gilt:
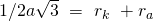
Durchlaufen wir die Raumdiagonale bis zur Mitte, erhalten wir wieder den Radius des äußeren Anions und den Radius des inneren Kations. Durch Umstellen erhalten wir:
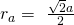
Setzen wir diese ins Verhältnis ergibt sich:
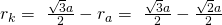
Den ersten Radienquotienten haben wir damit bestimmt. Schauen wir uns jetzt doch mal die Radienquotientenregel bei oktraedischer Struktur an.
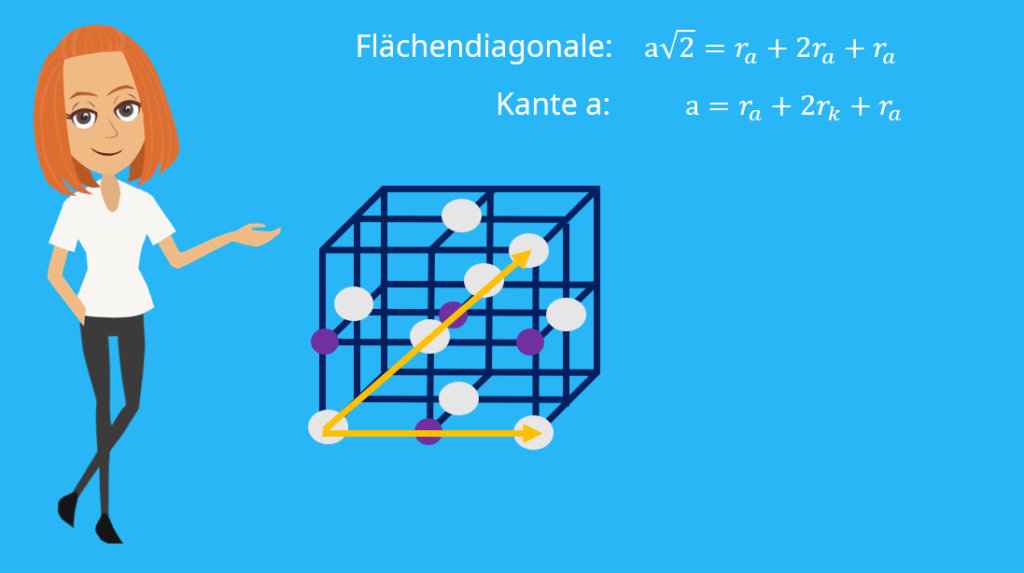
Rechnungsbeispiel – oktaedrische Struktur
Um die Flächendiagonale in der Gitterstruktur besser sehen zu können, müssen wir den Oktaeder erst einmal im Würfel erweitern. Du kannst noch ein zusätzliches Anion in der Mitte der Fläche erkennen.
Wir erhalten für die Flächendiagonale der Gitterstruktur:
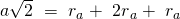
Auch für die zweite Gleichung müssen wir den Oktaeder wieder erweitert darstellen. Diese ergibt sich über die Kante a:
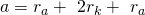
Durch Umstellen erhalten wir:
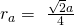
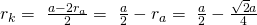
Den Radienquotienten erhalten wir damit mit:
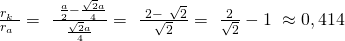
NaCl Struktur – Gitterstruktur Beispiel
Die Radien bestimmen wir aus einer Tabelle:
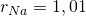 pm und
pm und 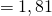 pm
pm
Der Radienquotient ergibt sich somit zu:
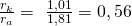
Nun betrachten wir die zuvor ermittelten Werte zu den jeweiligen Strukturen. Dabei musst du beachten, dass eine Verbindung in eine bestimmte Struktur eingeordnet wird, solange der nächstgrößere Wert noch nicht erreicht wurde. In diesem Fall handelt es sich also um eine oktaedrische Gitterstruktur, da 0,414 < 0,56 < 0,732.
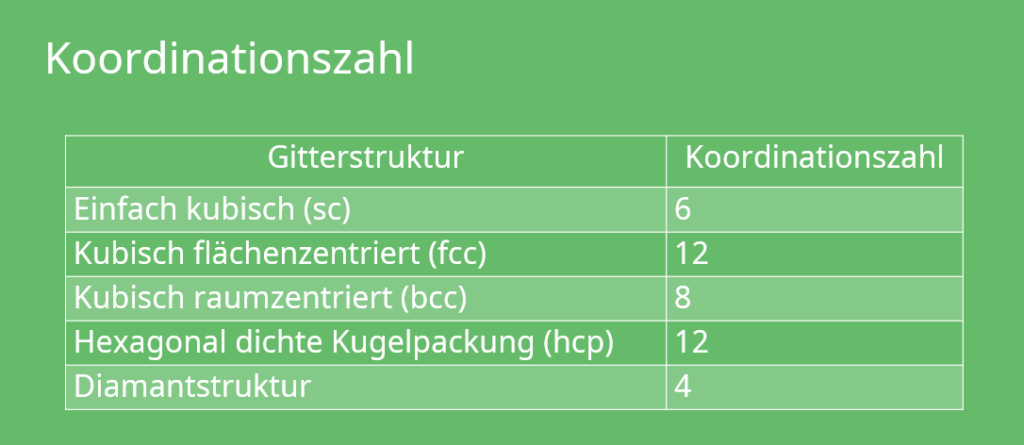
Diese Kennzahl zur Bestimmung der Gitterstruktur wird Koordinationszahl genannt.
Koordinationszahl
Um die Anzahl der nächsten Nachbarn einer Struktureinheit (d.h. Ion, Atom und Molekül) in einem Kristall zu finden, braucht man die Koordinationszahl. Damit kann eine Kristallstruktur durch die Angabe der Position ihrer Bausteine, also durch deren Koordination in der Einheitszelle beschrieben werden.
Wie du siehst, sind die Radienquotientenregel, Strukturtypen und die Koordinationszahl gar nicht so kompliziert, oder? Wenn du nochmal das Beispiel NaCl Struktur veranschaulicht haben möchtest, findest du dies in unserem Lernvideo.