PT1 Glied, Verzögerungsglied
In diesem Artikel möchten wir dir eine Zusammenfassung zum PT1-Glied geben. Wir erklären dir die Differenzialgleichung und Übertragungsfunktion die ein PT1 System beschreiben. Zusätzlich zeigen wir dir wie du die Sprungantwort bestimmst und das Bodediagramm zeichnest.
Schau dir am besten unser Video dazu an, in dem wir dir das wichtigste nochmal veranschaulichen.
Inhaltsübersicht
PT1-Glied einfach erklärt
Es handelt sich dabei um ein Übertragungsglied, das sich aus proportionalen Übertragungsverhalten mit Verzögerung 1. Ordnung zusammensetzt.
Systeme mit PT1 Verhalten werden auch als Systeme 1. Ordnung bezeichnet.
Differenzialgleichung des PT1 Glieds
Das PT1 Glied wird durch folgende Differenzialgleichung beschrieben:

Dabei ist 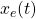 das Eingangssignal und
das Eingangssignal und  das Ausgangssignal des PT1 System,
das Ausgangssignal des PT1 System,
K ist der Proportionalitäts- bzw. Verstärkungsfaktor des Systems und T die Zeitkontante.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Übertragungsfunktion des PT1 Glieds
Die oben genannte Differenzialgleichung lässt sich im Bildbereich folgendermaßen ausdrücken:

Durch umstellen ergibt sich die Übertragungsfunktion des PT1 Glieds als Verhältnis von Ein- und Ausgangssignal:

Sprungantwort eines PT1 Glieds im Bildbereich
Die Sprungantwort  eines PT1 Systems im Bildbereich ergibt sich durch Multiplikation der Übertragungsfunktion mit
eines PT1 Systems im Bildbereich ergibt sich durch Multiplikation der Übertragungsfunktion mit  .
.


Die Ermittlung der Anfangs -und Endwerte kann unserem Artikel zur Sprungantwort entnommen werden.
Sprungantwort eines PT1 Glieds im Zeitbereich
Die Sprungantwort kann im Zeitbereich durch Rücktransformation aus dem Bildbereich ermittelt werden

In diesem Fall bietet es sich an eine Korrespondenztabelle für die Rücktransformation zu nutzen, dafür muss der Ausdruck aber zunächst in seine Partialbrüche zerlegt werden:



Die im Bildbereich ermittelten Anfangs und Endwerte lassen sich an der grafischen Darstellung der Sprungantwort des PT1 Gliedes ablesen. Das bedeutet auch, dass sich aus der Sprungantwort die Systemparameter als der Proportionalitätsfaktor K und die Zeitkonstante T ermitteln lassen.
Bodediagramm des PT1 Glieds
Für die Darstellung im Bodediagramm
ist es notwendig die Frequenzgangsfunktion des Systems zu ermitteln, dafür wird in der Übertragungsfunktion s durch  ersetzt:
ersetzt:

PT1 Glied: Amplitudengang
Im Folgenden ist der Amplitudengang zweier PT1 Systeme in asymptotischer Näherung dargestellt.
In Rot ist ein System mit der Übertragungsfunktion

mit 
Visualisiert. In Blau ein System mit K gleich 5 und T gleich 2.

mit 
Für niedrige Frequenzen entspricht das Amplitudenverhältnis K. Ab Erreichen der Eckfrequenz nimmt das Amplitudenverhältnis mit einer Steigung von 1:1 ab. Aus dem Amplitudengang lässt sich darauf schließen, dass es sich bei einem PT1 System um ein System mit Tiefpassverhalten handelt.
PT1 Glied: Phasengang
Im Phasengang markiert die Eckfrequenz den Punkt an dem die Phase -45 Grad beträgt. Ab diesem Punkt kann der Phasenverlauf mit einer Steigung von 45 Grad pro Dekade bis 0 bzw.- 90 Grad ergänzt werden. Ein PT1 Glied bewirkt also eine Phasenverschiebung von 0 Grad für Signale niedriger Frequenz und eine Phasenverschiebung von maximal -90 Grad für Signale hoher Frequenz.




