Bellman Ford Algorithmus
Du verstehst nicht, wie du mit dem Bellman-Ford-Algorithmus kürzeste Wege in Graphen finden kannst? In diesem Beitrag erklären wir dir genau das anhand von einfachen Beispielen.
Inhaltsübersicht
Bellman Ford Algorithmus – Kürzeste Wege
Mithilfe des Bellman-Ford-Algorithmus kannst du, ausgehend von einem Startknoten den kürzesten Weg zu allen anderen Knoten finden. Er kann außerdem auch mit negativen Kantengewichten umgehen.
Allgemeiner Ablauf des Bellman-Ford-Algorithmus
Doch wie läuft der Algorithmus ab? Das Ziel ist es, am Ende für jeden Knoten den Vorgänger zu finden, über den der Knoten am günstigsten erreicht wird.
Hierfür setzt du zuerst die Distanz zu jedem Knoten auf unendlich.
Dann wählst du einen Startknoten und setzt die Distanz zu diesem Knoten auf 0.
Für jede Kante musst du überprüfen, ob die Kosten zum Ausgangsknoten plus die Kosten der Kante geringer sind als die bisher bekannten Kosten zum Zielknoten. Sind die Kosten zum Ausgangsknoten unendlich, so kann die Kante aktuell keine Abkürzung liefern.
Findest du also eine Kante, die mit ihren Kosten plus den Kosten zum Ausgangsknoten kürzer zu einem Knoten, hier Knoten B, führt, dann hast du eine Abkürzung entdeckt.
Ist n die Anzahl der Knoten so müssen alle Knoten n – 1 mal überprüft werden. Danach musst du aber noch einmal jede Kante überprüfen. Aber warum, wir haben doch bereits den kürzesten Weg?
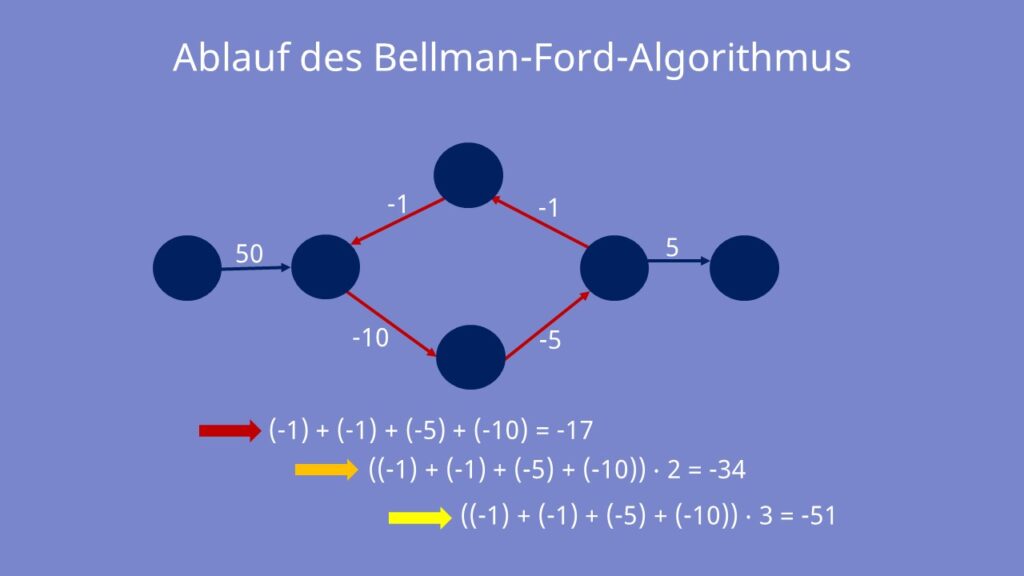
Um das zu verstehen schaust du dir am besten diesen Graphen an.
Wie du siehst, enthält der Graph zentral einen Zyklus . Zählen wir alle Kanten des Zyklus zusammen, erhalten wir als Ergebnis negative Kosten fürs Durchlaufen dieses Teilgraphen. Da der Weg mit jedem durchlaufenen Zyklus kürzer wird, kann man hier keinen eindeutigen kürzesten Weg festlegen.
Nachdem wir n – 1 mal jede Kante überprüft haben, testen wir ein letztes Mal jede Kante . Entsteht ein noch kürzerer Weg, dann enthält der Graph einen Zyklus mit negativem Gewicht und bricht ab.
Okay, soweit so gut. Doch woher weiß man nach dem Algorithmus, welcher Weg der kürzeste zu einem Knoten ist? Ganz einfach! Jeder Knoten speichert ab, über welchen Vorgänger der kürzeste Weg zu ihm verläuft. Man kann also den Weg vom Zielknoten rückwärts bis zum Startknoten verfolgen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Bellmann Ford Algorithmus Beispiel
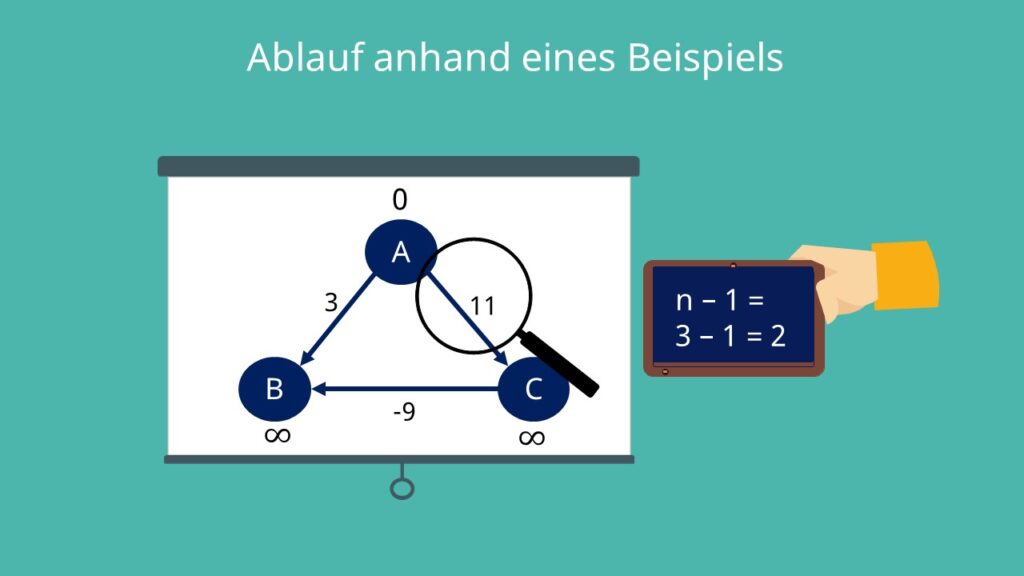
Genug Theorie, lass uns den Algorithmus an einem Beispiel testen. Wir wollen alle kürzesten Wege ausgehend von Knoten A finden.
Zuerst setzt du die Distanz zu allen Knoten auf unendlich, beziehungsweise die zum Startknoten A auf 0. Schreib einfach die aktuell kürzeste Distanz zu einem Knoten neben den Knoten selbst.
Alles klar! Nun überprüfen wir für jede Kante, ob es eine Abkürzung gibt. Wir haben 3 Knoten und müssen somit n – 1, also 2, mal alle Kanten überprüfen.
Beginnen wir mit der Kante AB mit dem Gewicht von 3. Wir zählen zum Kantengewicht noch die Kosten des Anfangsknoten der Kante hinzu. So kommen wir auf einen Weg von A zu B mit den Kosten 3. Das ist günstiger als unendlich und wir aktualisieren die Distanz.
Außerdem notieren wir uns den aktuellen Vorgänger von B.
Weiter geht es mit der Kante von C nach B. Diese startet bei einem Knoten, zu dem wir aktuell nur eine kürzeste Distanz von unendlich kennen. Somit liefert sie uns aktuell keine Abkürzung.
Zu guter Letzt betrachten wir noch die Kante AC: Null, die Distanz vom Ausgangsknoten, plus das Kantengewicht von 11 macht 11. Das ist kleiner als unendlich und wir aktualisieren die Distanz und den Vorgänger.
Unser erster Durchlauf ist beendet. Jetzt überprüfen wir erneut alle Kanten!
Beginnen wir wieder mit der Kante mit einem Gewicht von 3. Die Distanz zum Anfangsknoten plus das Kantengewicht ist nicht kleiner als die bekannte Distanz. Du musst also nichts ändern.
Jetzt überprüfen wir die Kante mit einem Gewicht von minus 9. Wir rechnen: Distanz zum Ausgangsknoten von 11 plus minus 9 gleich 2. Somit aktualisieren wir Distanz und Vorgänger von B.
Wie du siehst, liefert die Kante AC keine neue Abkürzung. Alle Kanten haben wir nun n – 1 mal getestet. Somit kommen wir jetzt zum letzten Teil des Algorithmus.
Jetzt musst du jede Kante ein letztes Mal überprüfen.
Finden wir eine Abkürzung enthält der Graph einen negativen Zyklus und wir müssen einen Fehler ausgeben. In diesem Fall sehen wir jedoch schnell, dass keine Abkürzungen mehr möglich sind, also sind wir an dieser Stelle fertig.
Doch wie findest du jetzt Beispielsweise den kürzesten Weg zu B heraus? Schauen wir nach, welcher Vorgänger von B uns das ermöglicht. Verfolgen wir den Weg bis zum Startknoten, erkennen wir, dass der kürzeste Weg von A nach B über den Knoten C führt und Kosten von 2 hat. Super!
Pseudocode des Bellman-Ford-Algorithmus
Du willst wissen, wie du den Bellman-Ford-Algorithmus implementieren kannst? Schau dir einfach diesen Pseudocode an:
n = Anzahl der Knoten
Für jeden Knoten:
Setze Distanz auf unendlich
Distanz von Startknoten = 0
Führe n – 1 mal aus:
Für jede Kante im Graph:
Wenn (Kantengewicht + Distanz zum Ausgangsknoten) < Distanz zum Zielknoten
Distanz zum Zielknoten = Kantengewicht + Distanz zum Ausgangsknoten
Vorgänger von Zielknoten = Ausgangsknoten
Für jede Kante im Graph:
Wenn (Kantengewicht + Distanz zum Ausgangsknoten) < Distanz zum Zielknoten
Gebe Fehler „Negativer Zyklus“ aus
Nun weißt du, wie du mithilfe des Bellman-Ford-Algorithmus, sogar in einem Graphen mit negativen Kantengewichten den kürzesten Weg findest.