Decision Tree
Du möchtest wissen, was ein Decision Tree ist und wozu man ihn verwendet? Das erfährst du hier und in unserem Video .
Inhaltsübersicht
Decision Tree Erklärung
Ein Decision Tree, zu Deutsch Entscheidungsbaum, ist ein Diagramm zur Entscheidungsfindung. Sein Aufbau erinnert an einen Baum. So besteht er aus Wurzeln, Knoten, Ästen und Blättern. Typischerweise werden Decision Trees zur Klassifizierung eingesetzt.
Einen Decision Tree baust du immer von oben nach unten auf, also hierarchisch. Am Anfang steht der Wurzelknoten. Dieser beinhaltet eine Aussage, auf dessen Basis eine Entscheidung zu treffen ist. Äste verbinden die Wurzel mit den jeweiligen Blättern.
Da die Aussage aus dem Wurzelknoten nur wahr oder falsch sein kann, handelt es sich um binäre Verzweigungen. Falls die Aussage wahr (True) ist, wird der linke Ast gewählt, andernfalls der rechte (False). In den Blättern findest du die Resultate. Zur Vereinfachung kannst du zukünftig die Beschriftung der Äste mit „True“ bzw. „False“ weglassen.
Anwendungsbereiche
Decision Trees lassen sich in verschiedenen Bereichen nutzen. Hier siehst du eine Übersicht der Anwendungsgebiete:
- Machine Learning , Statistik und Data Mining
- Analysegrundlage, z. B. Ergebnisse von Umfragen
- Automatische Gruppenzuordnung (Klassifikation)
- Vorhersage von stetigen Werten (Regression)
- Prüfung der Kreditwürdigkeit von Bankkunden
- Responseanalysen von Werbeaktivitäten
Außerdem kannst du Decision Trees als Algorithmus umsetzen (oftmals in Python ).
Wenn du komplexere Fragestellungen abbilden möchtest, kannst du mehrere Decision Trees zu einem Decision Forest kombinieren. Der macht die Klassifizierung genauer, ist aber nicht so intuitiv wie ein einzelner Decision Tree. Der wichtigste Algorithmus für einen Decision Forest ist der Random Forest.
Vom Problem zum Decision Tree
Wie genau kannst du Decision Trees erstellen? Schau es dir an einem einfachen Beispiel an.
Ein Fußballverein möchte wissen, aus welchen Gründen seine Spieler trainieren. Bei einer Befragung der Spieler sind Einflüsse wie ihre Motivation, ein anstehendes Spiel und ihr Gesundheitszustand aufgefallen. Du willst also feststellen, wie die Faktoren „Spiel steht an“, „Spieler ist motiviert“ und „Spieler ist gesund“ miteinander sowie mit der Folge „Spieler trainiert“ in Verbindung stehen. Folgende Daten liegen vor:
| Spiel steht an | Spieler ist motiviert | Spieler ist gesund | Spieler trainiert |
| Ja | Ja | Nein | Nein |
| Ja | Nein | Ja | Ja |
| Nein | Ja | Nein | Nein |
| Ja | Nein | Ja | Ja |
| Nein | Nein | Ja | Ja |
| Nein | Ja | Ja | Ja |
| Ja | Nein | Ja | Nein |
| Ja | Nein | Ja | Ja |
Zusammenhänge untersuchen
„Spieler trainiert“ soll also ein Blatt werden, die Positionierung der anderen Aussagen ist jedoch noch unbekannt. Da Decision Trees hierarchisch gegliedert sind, bestimmst du zunächst den Wurzelknoten. Im ersten Schritt untersucht du dazu, welcher Zusammenhang zwischen dem Ergebnis „Spieler trainiert“ und den einzelnen Aussagen besteht. Bevor du also den fertigen Decision Tree zeichnen kannst, stellst du separat kleine Decision Trees mit zwei Ebenen auf. Für die Aussage „Spiel steht an“ sieht das so aus:
Der Baum entsteht, indem du in der Tabelle überprüfst, ob die Aussage der Wurzel (in dem Fall, dass ein Spiel ansteht) mit Ja oder Nein beantwortet wurde. Ist Ja angegeben, nimmst du die linke Abzweigung, ansonsten die rechte. Im Anschluss schaust du dir an, was in derselben Zeile bei „Spieler trainiert“ ausgewählt wurde und notierst den Eintrag entsprechend unter Ja bzw. Nein. Sobald du alle Einträge der ersten Spalte gezählt hast, wiederholst du diesen Prozess für alle anderen Spalten der Tabelle. Du zeichnest zwei weitere kleine Decision Trees:
Den ersten Schritt hast du damit geschafft. Jetzt brauchst du noch eine Möglichkeit, die drei Aussagen zu vergleichen, damit du die geeignete Wurzel für deinen endgültigen Decision Tree findest.
Gini Impurity berechnen
Um zu entscheiden, welche Aussage die Wurzel bilden soll, bewertest du die drei entstandenen Decision Trees. Dafür verwendest du die Gini Impurity. Sie gibt an, wie fehleranfällig die Einordnung in „Spieler trainiert“ und „Spieler trainiert nicht“ ist:
bzw. Gini Impurity = 1 – ((Wahrscheinlichkeit für „Spieler trainiert“ Ja)2 + (Wahrscheinlichkeit für „Spieler trainiert“ Nein)2)
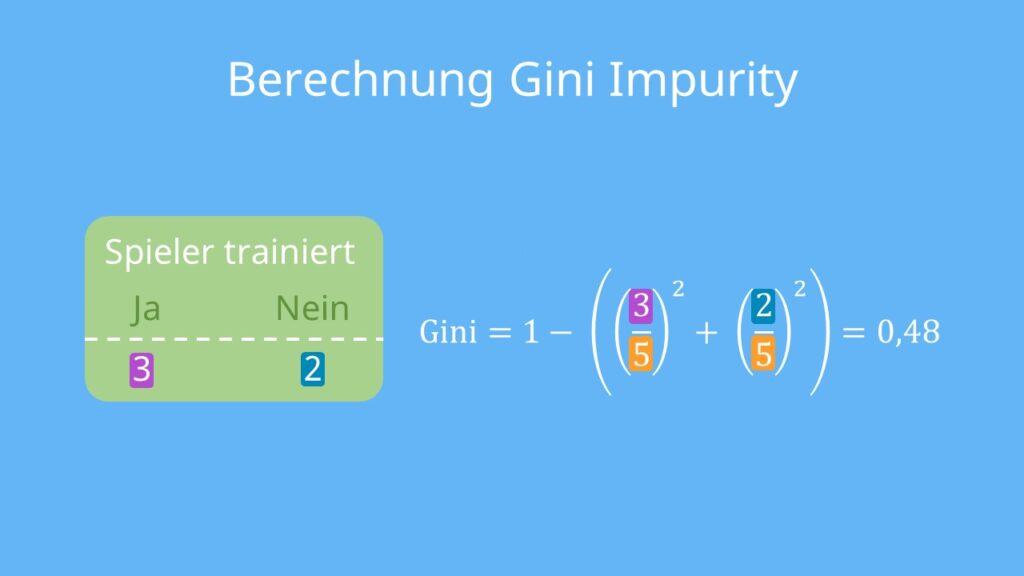
Berechne das Ganze einmal für den Baum mit der Wurzel „Spiel steht an“. Dafür bestimmst du die Gini Impurity für beide Blätter einzeln. Fangen wir mit dem linken Blattknoten an:
Die Gini Impurity des rechten Blattknotens 
ermittelst du analog. Aus den beiden Ergebnissen wird anschließend die Gini Impurity des gesamten Decision Trees errechnet:
Für unser Beispiel bedeutet das eingesetzt:
![\[\text{Gini Impurity} = (\frac{5}{5+3}) \cdot0,48 + (\frac{3}{3+5}) \cdot (\frac{4}{9}) \approx \textbf{0,47} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-7cee11f0922b8845dfa99cd4747952df_l3.png "Rendered by QuickLaTeX.com")
Das gleiche Vorgehen wendest du nun für die anderen beiden Decision Trees aus Schritt 1 an. Dabei kommst du auf folgende Werte:
| Spiel steht an | Spieler ist motiviert | Spieler ist gesund | |
| Gini Impurity | 0,47 | 0,37 | 0,21 |
Decision Tree aufstellen
Wenn du die Gini Impurities miteinander vergleichst, weist die des Decision Tree mit der Wurzel „Spieler ist gesund“ den geringsten Wert (0,21) auf. Also besteht hier die niedrigste Wahrscheinlichkeit für eine falsche Einordnung.
Damit hast du auch schon die Wurzel deines gesamten Decision Trees bestimmt! Da die Gini Impurity des rechten Pfades bereits 0 beträgt, kannst du gleich einen Blattknoten einfügen. Die Einordnung ist hier also fehlerfrei. Jeder Spieler, der nicht gesund war, hat auch nicht trainiert.
Die weiteren Ebenen und Pfade errechnest du nach dem selbem Prinzip. Einziger Unterschied besteht darin, dass es jetzt eine Vorbedingung gibt. Beim Vervollständigen des linken Pfades betrachtest du also nur noch die Zeilen der Tabelle, die in der Spalte „Spieler ist gesund“ Ja enthalten.
Ansonsten gehst du wie beim Ermitteln der Wurzel vor, indem du die Gini Impurity der verschiedenen weiteren Pfadverläufe vergleichst. Beachte dabei, dass auch ein direkter Blattknoten als Pfad infrage kommt. Dessen Gini Impurity schließt du also in deinen Vergleich mit ein.
Wenn du alles fertig gerechnet hast, kommst du zu folgendem Ergebnis:
Wie du siehst, ist selbst unser einfaches Modell nicht unfehlbar. In einem der Blätter (1/3) kann keine hundertprozentige Kategorisierung erfolgen. Vor allem beim Einsatz von Decision Trees im Machine Learning wird dir dieses Problem häufig begegnen.
Vor- und Nachteile zusammengefasst
Super! Jetzt kannst du Decision Trees aufstellen. Was aber sind die Vor- und Nachteile von Decision Trees? Hier eine Übersicht:
| Vorteile | Nachteile |
|
Hierarchischer Aufbau |
Leichte Änderungen der Trainingsdaten kann zu sehr unterschiedlichen Ergebnissen führen (instabil) |
| Theoretisch beliebig viele Entscheidungsebenen implementierbar | Algorithmus erfordert durchschnittlich hohe Trainingszeit |
Machine Learning
Du willst noch mehr über das Einsatzgebiet der Decision Trees erfahren? Dann schaue dir direkt unser Video zu Machine Learning an.
