Gleichgewichtslage berechnen
In diesem Beitrag behandeln wir die Gleichgewichtslagen noch einmal vertiefender. Zuerst schauen wir die Theorie an, bevor wir uns dem Beispiel eines Pendels widmen. Den kompletten Inhalt findest du auch in unserem Video , in kürzester Zeit zusammengefasst.
Inhaltsübersicht
Gleichgewichtslagen
Als erstes fassen wir noch einmal die Grundlagen zusammen:
Um herauszufinden, ob und wo ein System ein stabiles Gleichgewicht, ein indifferentes Gleichgewicht oder ein labiles Gleichgewicht hat, betrachten wir in der Regel das Potential beziehungsweise die Arbeit, aus der sich das Potential ergibt. Dazu überlegen wir uns vorher, welche Bewegung das System vollführen kann und stellen eine Gleichung für die Arbeit in Abhängigkeit einer Laufvariablen auf, die die Bewegung beschreibt.
Als nächstes ermitteln wir die Gleichgewichtslage des Systems, indem wir die Gleichung für die Arbeit ableiten, gleich null setzen und dann lösen. Vergleichbar ist das mit der Ermittlung der Extrempunkte einer Funktion. Als letztes überprüfen wir, ob die jeweilige Gleichgewichtslage stabil ist. Dazu leiten wir die Gleichung der Arbeit ein weiteres Mal ab und setzen unsere gefundenen Ergebnisse in die zweite Ableitung ein. Um nun eine Aussage über die Stabilität machen zu können, betrachten wir das Vorzeichen. Es gilt:
Wenn die zweite Ableitung kleiner null ist, handelt es sich um ein stabiles Gleichgewicht. Ist sie gleich null, können wir von einem indifferenten Gleichgewicht ausgehen und ist sie größer null, dann ist das Gleichgewicht labil. Wichtig ist, dass  nur stellvertretend für die Laufvariable steht und nicht generell verwendet werden kann. Das klingt zwar komplex, aber du wirst gleich sehen, dass es gar nicht so schwer ist.
nur stellvertretend für die Laufvariable steht und nicht generell verwendet werden kann. Das klingt zwar komplex, aber du wirst gleich sehen, dass es gar nicht so schwer ist.
Beispiel Pendel
Nachdem wir die Theorie in Bezug auf das stabile Gleichgewicht, das indifferente Gleichgewicht und das labile Gleichgewicht wieder parat haben, betrachten wir nun ein weiteres Beispiel zur Gleichgewichtslage: Ein einfaches Pendel mit der Länge  , an dem am Ende eine Masse mit
, an dem am Ende eine Masse mit  hängt. Wir gehen davon aus, dass das Pendel eine starre Stange ist und sich das System logischerweise im Erdschwerefeld befindet. Das heißt, wir haben eine Erdbeschleunigung von
hängt. Wir gehen davon aus, dass das Pendel eine starre Stange ist und sich das System logischerweise im Erdschwerefeld befindet. Das heißt, wir haben eine Erdbeschleunigung von  . Zu Beginn ist das Pendel in der Waagerechten festgehalten.
. Zu Beginn ist das Pendel in der Waagerechten festgehalten.
Wenn wir das Pendel nun loslassen, dreht es sich um die Befestigung. Dementsprechend nehmen wir als Laufvariable den Winkel  , um den sich das Pendel gegenüber der Ausgangslage bewegt.
, um den sich das Pendel gegenüber der Ausgangslage bewegt.
Als erstes stellen wir die Gleichung für die Arbeit auf: Da in unserem Fall nur die Gewichtskraft der Masse angreift, ist diese relativ schnell aufgestellt. Die Gewichtskraft zeigt immer nach unten. Deshalb müssen wir nur den Weg  nach unten betrachten. Dieser ist natürlich wiederrum abhängig von
nach unten betrachten. Dieser ist natürlich wiederrum abhängig von  und ergibt sich zu:
und ergibt sich zu:

Daraus resultiert dann für die Arbeit:
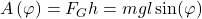
 ist dabei die Gewichtskraft gleich
ist dabei die Gewichtskraft gleich  .
.
Nachdem wir eine Gleichung für die Arbeit haben, bilden wir die erste Ableitung nach unserer Laufvariablen  und erhalten:
und erhalten:

Die erste Ableitung setzen wir jetzt gleich null und suchen Lösungen für  :
:
Das heißt, unsere jeweilige Gleichgewichtslage ist bei  gleich
gleich  senkrecht UNTER der Aufhängung und bei
senkrecht UNTER der Aufhängung und bei  gleich
gleich  senkrecht ÜBER der Aufhängung.
senkrecht ÜBER der Aufhängung.
Zum Schluss treffen wir noch eine Aussage über die Stabilität. Dazu bilden wir die zweite Ableitung:

Jetzt müssen wir nur noch jeweils die gefundene Gleichgewichtslage einsetzen. Wie du bereits weißt, gilt:
 und
und 
Damit ergibt sich für die Gleichgewichtslage:
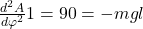

Erinnern wir uns jetzt zurück an die Bedingungen über die Stabilität, erkennen wir, dass  gleich 90° ein stabiles Gleichgewicht ist, da das Vorzeichen in jedem Fall negativ ist und
gleich 90° ein stabiles Gleichgewicht ist, da das Vorzeichen in jedem Fall negativ ist und  gleich 270° ein instabiles Gleichgewicht ist, da das Vorzeichen auch hier nicht wechseln kann. Du erkennst, dass wir keine Abhängigkeit vom System, sondern feste Winkel und damit Positionen haben. Das deckt sich auch mit unserer physikalischen Intuition.
gleich 270° ein instabiles Gleichgewicht ist, da das Vorzeichen auch hier nicht wechseln kann. Du erkennst, dass wir keine Abhängigkeit vom System, sondern feste Winkel und damit Positionen haben. Das deckt sich auch mit unserer physikalischen Intuition.



