Boolesche Algebra
Du möchtest wissen, was die Boolesche Algebra ist? Im Folgenden zeigen wir dir die verschiedenen Gesetze und Rechenregeln der booleschen Algebra.
Inhaltsübersicht
Boolesche Algebra einfach erklärt
Die boolesche Algebra wird auch häufig als boolescher Verband bezeichnet und ist ein mathematisches System, das auf Logik basiert. Sie wurde nach George Boole benannt. Dieser erfand die algebraischen Strukturen um komplexe boolesche Ausdrücke zu vereinfachen und wandte diese erstmals auf die Aussagenlogik an. Damit lässt sich in einem Schaltkreis beispielsweise die Zahl der benötigten Logikgatter reduzieren.
Grundsätzlich werden in der booleschen Algebra Variablen benutzt, die nur zwei mögliche Werte annehmen können, entweder eine logische „0“ oder eine logische „1“. Ein boolescher Ausdruck besteht aus beliebig vielen Variablen, die jeweils anders bezeichnet werden. Wir verwenden hierfür die Buchstaben A, B, C, …etc. aus dem Alphabet.
Boolesche Algebra Rechenregeln: Multiplikation
Schauen wir uns zunächst einen einfachen Rechenvorgang in der booleschen Algebra an: die Multiplikation.




Wie du sehen kannst, funktioniert diese genauso wie die Multiplikation mit realen Zahlen. Sie ist das Äquivalent zur Und-Operation bei den Logikgattern. Deshalb kann ein Produkt von zwei Variablen A und B auch als A und B geschrieben werden.

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Addition
Die zweite wichtige Rechenart ist die Addition. Für zwei Variablen A und B, welche beide die Werte 0 und 1 annehmen können, ergeben sich folgende Optionen:
Wenn eine Variable 1 ist, ist das Ergebnis auch 1. Wenn du dich noch nicht mir boolscher Algebra beschäftigt hast, bist du von der letzten Gleichung eventuell etwas überrascht. Du kannst dir das einfach folgendermaßen vorstellen: 0 steht für „nichts“ und 1 für „etwas“. Hast du zweimal „nichts“, hast du auch insgesamt nichts. Für den Fall, dass du einmal „nichts“ plus einmal „etwas“ hast, hast du etwas. Hast du zweimal „etwas“, hast du auch insgesamt „etwas“. Damit entspricht die boolesche Addition der Oder-Operation bei den Logikgattern.

Boolesche Logik: Grundlegende Gesetze
Jetzt machen wir mit den grundlegenden Gesetzen der booleschen Algebra weiter. Wie in der normalen Algebra, existieren in der booleschen Algebra auch das Kommutativ-, das Assoziativ- und das Distributivgesetz.
Schauen wir uns zuerst das Kommutativgesetz für Addition und Multiplikation an. Es gilt:


Auch hier entsprechen die Gesetze denen der normalen Algebra. Dasselbe gilt für die Assoziativgesetze.


…und auch für das Distributivgesetz!

Boolesche Algebra Gesetze
Nun, da wir die grundlegenden Rechenregeln behandelt haben, können wir uns die booleschen Algebra Gesetze ansehen. Wir beginnen mit folgenden Regeln:



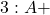




Diese ersten vier Gesetze ergeben sich aus den Grundsätzen, die für die Addition gelten. Egal ob A den Wert 1 oder 0 annimmt, bei der Addition von 0 ergibt sich immer der ursprünglicher Wert A und bei der Addition von 1 ergibt sich immer 1. Bei zwei gleichen Werten, also entweder 0 plus 0 oder 1 plus 1, ergibt sich auch wieder der ursprüngliche Wert A. Bei zwei ungleichen Werten 0 und 1 ergibt sich in der boolschen Addition immer 1.








Die Gesetze fünf und sechs lassen sich von den Multiplikationsregeln ableiten und entsprechen den Rechengesetzen der normalen Algebra. Bei Gesetz 7 haben wir wieder 2 gleiche Werte, deshalb ergibt sich wieder der Wert A. Multiplizieren wir A und Nicht A, muss ein Wert 0 sein und das Ergebnis ist somit auch 0.
Boolesche Algebra Regeln 9-12
Nicht nicht A entspricht A. Doppelte Negierungen heben sich also auf.
Das zehnte boolesche Theorem können wir mit dem Distributivgesetz beweisen. Wir klammern A aus. Wie wir aus dem zweiten booleschen Gesetz wissen, ist eine beliebige Variable plus 1 immer 1. Das heißt das Ergebnis ist A.
Schauen wir uns nun noch 2 weitere Theoreme an. Hier können wir mit Hilfe der 7. Regel ausklammern. Wir wissen bereits, dass A plus nicht A eins ergibt, also lautet das Ergebnis A plus B.
Nun schauen wir uns das letzte Theorem an.
Auch hier können wir das Theorem wieder mit Hilfe anderer Regeln beweisen. Zuerst multiplizieren wir aus. Dann klammern wir A bei den mittleren Termen aus. Wir haben bereits gelernt, dass A mal A A ergibt. Wir ziehen A an den Anfang und sehen nun, dass der Term in der Klammer 1 ergibt. Somit kommen wir auf unser Ergebnis A plus B mal C.
Nun kennst du die Grundregeln der booleschen Algebra und kannst sie auf Schaltkreise in der Digitaltechnik anwenden.




