Gleichverteilung
Hier erfährst du alles zu Gleichverteilungen. Zuerst wird die diskrete Gleichverteilung behandelt, dann die stetige Gleichverteilung. Unter anderem werden die Dichtefunktion, die Verteilungsfunktion, der Erwartungswert und die Varianz für den diskreten und stetigen Fall der Wahrscheinlichkeitsverteilung anhand eines anschaulichen Beispiels berechnet.
Du willst lieber gleich alles verstehen, ohne diesen Artikel zu lesen? Dann sind unsere Videos zur diskreten Gleichverteilung und zur stetigen Gleichverteilung genau das Richtige für dich!
Inhaltsübersicht
Gleichverteilung einfach erklärt
Die Gleichverteilung ist eine Wahrscheinlichkeitsverteilung der Statistik. Es wird zwischen der diskreten Gleichverteilung und der stetigen Gleichverteilung unterschieden. Im stetigen Fall wird diese Verteilung auch Uniformverteilung genannt. Grundlegend unterscheiden sich die beiden darin, dass im diskreten Fall alle möglichen Ergebnisse dieselbe Wahrscheinlichkeit haben und im stetigen Fall die Dichte konstant ist.
Diskrete Gleichverteilung
Die diskrete Gleichverteilung ist eine der einfachsten Verteilungen der Wahrscheinlichkeitsrechnung. Sie liegt vor, wenn eine Zufallsvariable diskret ist, sie also nur eine endliche Zahl an möglichen Ergebnissen hat und jedes Ergebnis dieselbe Wahrscheinlichkeit hat.
Zunächst beschränken wir uns jedoch auf ein Beispiel einer diskreten Gleichverteilung, nämlich Zufallsexperimente, deren mögliche Ergebnisse durch ganze Zahlen zwischen a und b dargestellt werden können.
Ein klassisches Anwendungsbeispiel ist der Wurf eines, natürlich ungezinkten, Würfels. Die Wahrscheinlichkeiten sind hier gleichverteilt. Gleichverteilt heißt, dass diesem Beispiel jedes mögliche Ergebnis zwischen a gleich 1 und b gleich 6 mit derselben Wahrscheinlichkeit auftritt.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Gleichverteilung Wahrscheinlichkeit
Fangen wir mit den Wahrscheinlichkeiten der disktreten Gleichverteilung und der dazugehörigen Wahrscheinlichkeitsfunktion an, welche die „Dichtefunktion“ für den diskreten Fall ist. Beim Würfelwurf hat jedes Ergebnis die Wahrscheinlichkeit  . Die Funktion sieht dann wie folgt aus:
. Die Funktion sieht dann wie folgt aus:
Die Formel sieht vielleicht etwas kompliziert aus, ist aber eigentlich ganz einfach. Für jedes gleichverteilte Ergebnis zwischen 1 und 6 ist die Wahrscheinlichkeit gleich  . Da bei einem Würfelwurf ja gar nichts anderes möglich ist, ist die Wahrscheinlichkeit für sonstige Ergebnisse gleich 0.
. Da bei einem Würfelwurf ja gar nichts anderes möglich ist, ist die Wahrscheinlichkeit für sonstige Ergebnisse gleich 0.
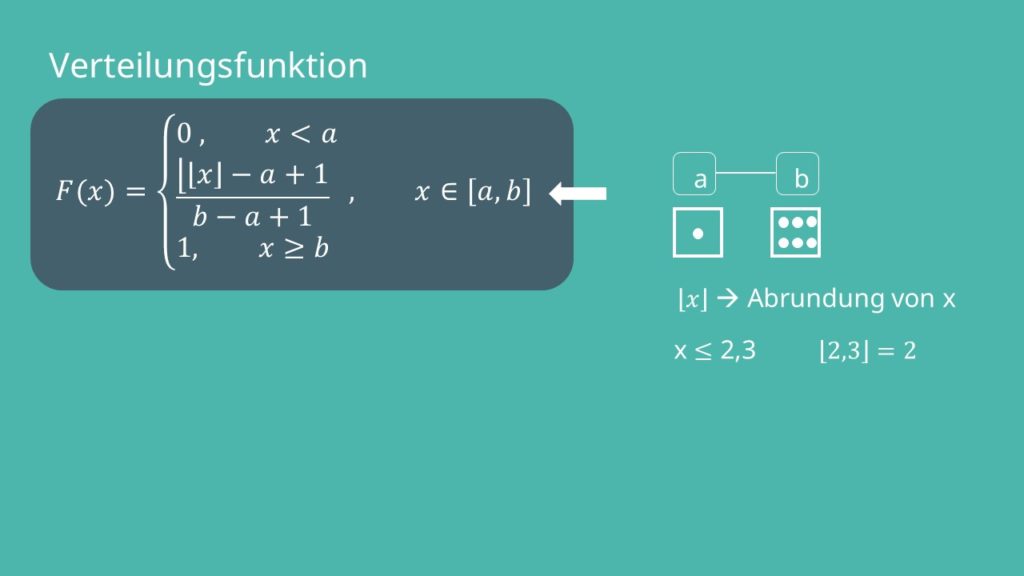
Gleichverteilung Verteilungsfunktion: diskret
Im allgemeinen Fall sieht die Verteilungsfunktion etwas seltsam aus:

Die beiden geraden Linien |…| stehen für die Mächtigkeit der Menge. Suchen wir also zum Beispiel die Wahrscheinlichkeit für ein Ergebnis  , zählen wir alle möglichen Ergebnisse, die kleiner gleich 4 sind, bei einem Würfelwurf also 1,2,3 und 4 auf. Das heißt unsere Menge im Zähler hat 4 Elemente. Somit gilt also:
, zählen wir alle möglichen Ergebnisse, die kleiner gleich 4 sind, bei einem Würfelwurf also 1,2,3 und 4 auf. Das heißt unsere Menge im Zähler hat 4 Elemente. Somit gilt also:

Wie du weißt, gibt die Verteilungsfunktion immer die Wahrscheinlichkeit dafür an, dass ein Ergebnis kleiner gleich x herauskommt. Der erste Abschnitt gilt für Ergebnisse kleiner a, also beim Würfelwurf zum Beispiel das Ergebnis 0. Da es gar nicht möglich ist, dieses Ergebnis zu erhalten ist die Wahrscheinlichkeit also gleich 0. Der zweite Abschnitt gilt für Ergebnisse zwischen a und b, also in unserem Fall zwischen 1 und 6. [x] steht für die Abrundung von x. Die Verteilungsfunktion des Beispiels der diskreten Gleichverteilung ist folglich ebenfalls dreigeteilt:
Erwartungswert Gleichverteilung: diskret
Der Erwartungswert der diskreten Gleichverteilung ist in diesem Fall ganz einfach der Mittelwert aus a und b, also a plus b geteilt durch 2.

Im allgemeinen Fall gilt diese Formel für den Erwartungswert:

Varianz Gleichverteilung: diskret
Die Formel der Varianz im hier behandelten Fall lautet wie folgt:

Für die Varianz der diskreten Gleichverteilung im allgemeinen Fall gilt diese Formel:

Hier findest du nochmal alle wichtigen Formeln, für das betrachtete Beispiel:
Allgemein sind die Formeln der diskreten Gleichverteilung folgende:
Stetige Gleichverteilung
Die stetige Gleichverteilung ist eine Wahrscheinlichkeitsverteilung, die auf einem Intervall eine konstante Wahrscheinlichkeitsdichte hat. Jeder denkbare reelle Wert der Zufallsvariable ist in einem vorgegebenen Intervall gleich wahrscheinlich. Daher kommt auch der Name uniforme Verteilung.
Das erscheint dir noch nicht ganz verständlich?
Dann stell dir das Ganze mit einem Beispiel vor. Nehmen wir an, es ist Samstagnacht und du bist auf dem Weg vom Club nach Hause.
Du weißt, dass die S-Bahn nachts nur noch stündlich fährt, aber hast die genauen Abfahrtszeiten vergessen. Läufst du also auf gut Glück zur Station ist deine Wartezeit eine stetige Gleichverteilung zwischen a gleich null und b gleich sechzig. Denn zwischen null und sechzig Minuten sind alle Zeiten uniform verteilt. Das heißt du kannst jede erdenkliche Zeit warten, zum Beispiel auch 5,2343 Minuten. Ist doch logisch, oder?
In Kurzschreibweise sieht das Ganze dann so aus:

bzw. allgemein 
Erwartungswert Gleichverteilung: stetig
Den Erwartungswert im stetigen Fall kannst du mit folgender Formel berechnen:

Du siehst, dass der Erwartungswert also genau in der Mitte von a und b liegt.
Varianz Gleichverteilung: stetig
Die Varianz der stetigen Gleichverteilung kannst du mit dieser Formel ausrechnen:
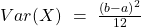
Keine Sorge, wir ersparen dir hier die mathematische Herleitung. Am besten du lernst diese Formeln auswendig oder schreibst sie auf dein Formelblatt.
Dichtefunktion Gleichverteilung
Die Dichtefunktion der stetigen Gleichverteilung stellst du wie folgt dar:
Die Dichtefunktion kann grob in zwei Teile aufgeteilt werden. Innerhalb des betrachteten Intervalls haben alle Werte – hier auch Träger genannt – die gleiche Wahrscheinlichkeit. Diese wird mit ausgedrückt. Außerhalb diesen Bereichs ist die Wahrscheinlichkeit immer gleich 0. Somit lässt sich auch die zweiteilige Definition der Dichtefunktion der stetigen Gleichverteilung erklären.
Gleichverteilung Verteilungsfunktion: stetig
Die zugehörige Verteilungsfunktion ist dreiteilig definiert:
Auch das lässt sich ganz leicht erklären, wenn du den Graphen betrachtest. Innerhalb des betrachteten Intervalls ist die Verteilungsfunktion eine Gerade, welche konstant von 0 bis 1 ansteigt. Das liegt daran, dass die kumulierten Wahrscheinlichkeiten gleichmäßig verteilt sind. An der Stelle x=a ist die Funktion gleich 0 und nähert sich kontinuierlich dem Wert 1mit Annäherung an b.
Stetige Gleichverteilung Beispiel
Greifen wir unsere Überlegung von oben wieder auf. Du bist gerade tot müde auf dem Weg zur S-Bahnstation. Da du so schnell wie möglich nach Hause in dein Bett möchtest und genau weißt, dass du bei einer Wartezeit von mehr als 15 Minuten am Bahnsteig einschlafen wirst, rechnest du aus, wie wahrscheinlich es ist, dass du weniger als 15 Minuten warten musst.
Dazu benutzt du die Formel der Verteilungsfunktion und setzen unsere Werte ein.
Die Wahrscheinlichkeit, dass du höchstens 15 Minuten warten musst, beträgt also 25 Prozent. Schade, du verbringst die Nacht also voraussichtlich am Bahnsteig.
Aber Spaß bei Seite! Du kannst jetzt gerne noch den Erwartungswert und die Varianz selbst berechnen, indem du die Werte in die Formeln einsetztst. Die Lösungen geben wir dir vor:


Das wars auch schon zur Gleichverteilung! Du weißt jetzt, wie man sie berechnet und dass du den Club nächstes Mal früher verlassen solltest.