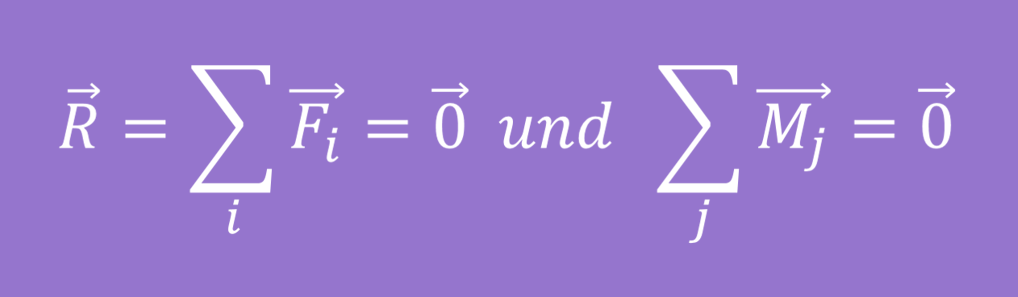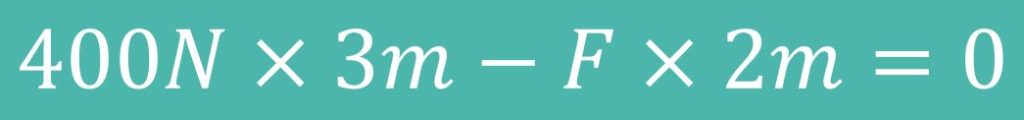Kräftegleichgewicht und Momentengleichgewicht
In diesem Beitrag geht es um die Gleichgewichtsbedingungen in der Statik. Dabei behandeln wir das Momentengleichgewicht und das Kräftegleichgewicht. Dazu gehen wir zunächst auf die Kraft und das Moment kurz ein, um dann die Gleichgewichtsbedingung herzuleiten. Im Anschluss erklären wir dir noch das Superpositionsprinzip und berechnen ein Beispiel zum Momentengleichgewicht.
Inhaltsübersicht
Gleichgewichtsbedingungen in der Statik
In der Statik beruhen die meisten Rechenwege, Herleitungen oder Annahmen auf der sogenannten Gleichgewichtsbedingung. Vereinfacht heißt das, dass sich ein Körper unter Last nicht bewegt. Dabei können am Körper sowohl Momente als auch Kräfte als Last wirken. Addieren sich, die auf das System wirkende Kräfte oder Momente zu null auf, so entsteht das Momenten– oder auch Kräftegleichgewicht.
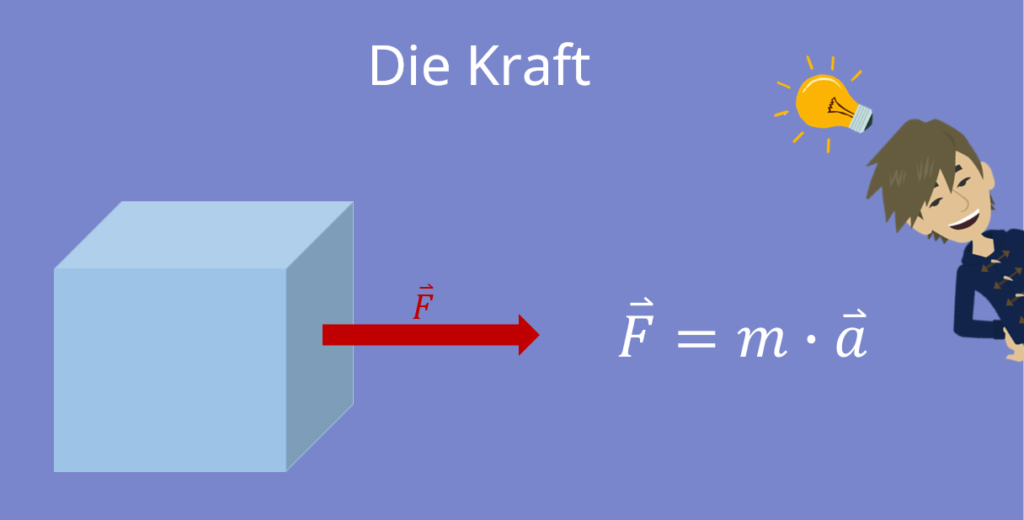
Formel der Kraft
Die grundlegenden Zusammenhänge zur Kraft lernst du in unserem Video für die Newtonschen Axiome
. Im Allgemeinen wird eine Kraft über die Beschleunigung 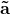 eines Körpers und dessen Masse
eines Körpers und dessen Masse 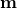 definiert. Leider ist das Messen einer Kraft
definiert. Leider ist das Messen einer Kraft 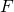 nicht so einfach möglich und wird daher über folgende Formel berechnet:
nicht so einfach möglich und wird daher über folgende Formel berechnet:
Der Vektorpfeil auf dem Formelzeichen der Kraft 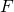 bedeutet, dass es sich um eine gerichtete Größe handelt.
bedeutet, dass es sich um eine gerichtete Größe handelt. 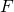 besitzt also eine sogenannte Wirkungslinie. Vereinfacht gesagt wirkt die Kraft in eine Richtung, die wiederum abhängig von der Beschleunigung ist.
besitzt also eine sogenannte Wirkungslinie. Vereinfacht gesagt wirkt die Kraft in eine Richtung, die wiederum abhängig von der Beschleunigung ist.
Formel des Moments
Was eine Kraft ist, wusstest du vielleicht schon vorher, doch du fragst dich jetzt, was man unter einem Moment versteht? Auch das könnte dir aus der Schule bekannt sein, jedoch nicht unter diesem Namen. Verwendet wird das nämlich auch beim Hebelgesetz, nur in vereinfachter Form.
Wichtig ist, dass ein Moment immer nur bezüglich eines Punktes definiert ist. Allgemein wird ein Moment durch folgende Formel beschrieben:
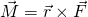
Dabei entspricht 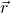 dem Ortsvektor von einem beliebigen Punkt zur Wirkungslinie der Kraft. Hier ist es egal welcher Punkt auf der Wirkungslinie gewählt wird. In der Regel ist es aber der Angriffspunkt der Kraft.
dem Ortsvektor von einem beliebigen Punkt zur Wirkungslinie der Kraft. Hier ist es egal welcher Punkt auf der Wirkungslinie gewählt wird. In der Regel ist es aber der Angriffspunkt der Kraft.
Momentengleichgewicht und Kräftegleichgewicht
Du fragst dich jetzt sicher, was so ein Moment genau macht. Das Hebelgesetz ist auch ein Spezialfall der Momentenrechnung. Deshalb betrachten wir nun eine Wippe: an einem Ende greift eine Kraft, z.B. in Form der Gewichtskraft eines Kindes, an. Unser Bezugspunkt ist die Aufhängung der Wippe. Stellen wir uns nun vor, dass die Aufhängung hoch genug angebracht wurde, damit die Wippe den Boden nicht berühren kann. Dann würde die Wippe sich um die Aufhängung drehen. Also erzeugt ein Moment nur eine Drehung um den gewählten Bezugspunkt. Auch hier ist grundsätzlich eine Drehung um jede beliebige Achse möglich.
Wahrscheinlich denkst du dir jetzt: Schön, dass es Kräfte und Momente gibt, aber was hat das mit den Gleichgewichtsbedingungen, dem Momentengleichgewicht und dem Kräftegleichgewicht zu tun? Wie du vielleicht bemerkt hast, haben sowohl Kraft als auch Moment etwas mit Bewegung zu tun. Bei der Gleichgewichtsbedingung geht es jetzt darum, dass keine Bewegung stattfindet, also sich das beobachtete Objekt im Gleichgewicht befindet. Daraus folgt, dass am Ende auf den Körper keine resultierende Kraft und kein resultierendes Moment wirken darf.
Superpositionsprinzip: Addition der Kräfte und Momente
Durch das Superpositionsprinzip der Mechanik, lassen sich die gesamten Momente und Kräfte jeweils durch einfache Addition errechnen. Falls du genaueres zu diesem Video wissen willst, haben wir dir hier ein extra Video dazu verlinkt. Daher lässt sich folgende Formulierung für die Gleichgewichtsbedingungen aufstellen:
Hierbei ist 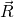 die resultierende Kraft, die durch die Addition der Kräfte entsteht. Du musst dabei beachten, dass sowohl Kraft als auch Moment vektoriell addiert werden müssen. Das führt zur folgenden, komponentenweisen Darstellung:
die resultierende Kraft, die durch die Addition der Kräfte entsteht. Du musst dabei beachten, dass sowohl Kraft als auch Moment vektoriell addiert werden müssen. Das führt zur folgenden, komponentenweisen Darstellung:
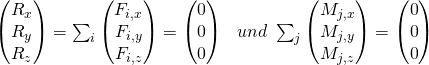
Es ergeben sich also 6 Gleichungen, um 6 Unbekannte zu bestimmen. Diese Gleichgewichtsbedingung gilt an jedem Punkt innerhalb eines Systems, das sich im Gleichgewicht befindet. Bei den Momenten ist zu beachten, dass diese sowohl von außen eingebrachte, als auch durch die Kräfte resultierende Momente beinhalten.
Berechnung des Momentengleichgewichts
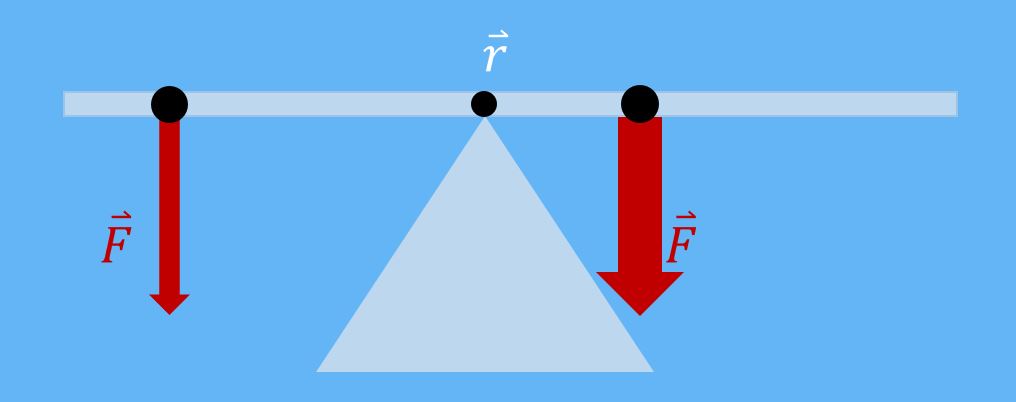
Das sieht natürlich jetzt sehr abstrakt aus. Also betrachten wir nun wieder die Wippe: jede Seite der Wippe ist nun 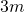 lang und auf einer Seite sitzt ein Kind, welches eine Gewichtskraft von 400 Newton besitzt. Auf der anderen Seite sitzt ein weiteres Kind, jedoch nur in
lang und auf einer Seite sitzt ein Kind, welches eine Gewichtskraft von 400 Newton besitzt. Auf der anderen Seite sitzt ein weiteres Kind, jedoch nur in 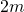 Abstand zum Drehpunkt der Wippe. Welche Kraft muss nun dort angreifen, damit die Wippe im Gleichgewicht ist?
Abstand zum Drehpunkt der Wippe. Welche Kraft muss nun dort angreifen, damit die Wippe im Gleichgewicht ist?
Um das zu lösen, stellen wir ein Momentengleichgewicht um die Aufhängung auf:
Damit sich die Wippe nicht bewegt, brauchen wir also eine Gegenkraft von 600 Newton. Die angreifenden Kräfte müssen sich zu null addieren.
Wie du siehst ist dieses einfache Prinzip überall zu finden. Zum Beispiel beim Tauziehen. Auch dort ist ein Kräftegleichgewicht zu beobachten: Zwei Personen ziehen mit gleicher Kraft an einem Seil, weshalb sich keine der Personen bewegt. Nur wenn eine Person stärker ist, also eine größere Kraft ausübt, setzt eine Bewegung ein und es gibt kein Kräftegleichgewicht mehr.
Das Momentengleichgewicht ist ebenfalls bei ganz einfachen Dingen zu entdecken. Nehmen wir einfach einen Stift zur Hand und versuchen diesen auf einem Finger auszubalanzieren. Dabei versuchen wir intuitiv ein Momentengleichgewicht aufzustellen, damit der Stift nicht runterfällt.