Loslager und Festlager
Festlager und Loslager werden in der Mechanik neben der festen Einspannung häufig zur Ermittlung von angreifenden Kräften betrachtet. Im nachfolgenden Beitrag geben wir dir einen Überblick, was man aus statischer Sicht unter den Begriffen Festlager und Loslager versteht.
Inhaltsübersicht
Lager einfach erklärt
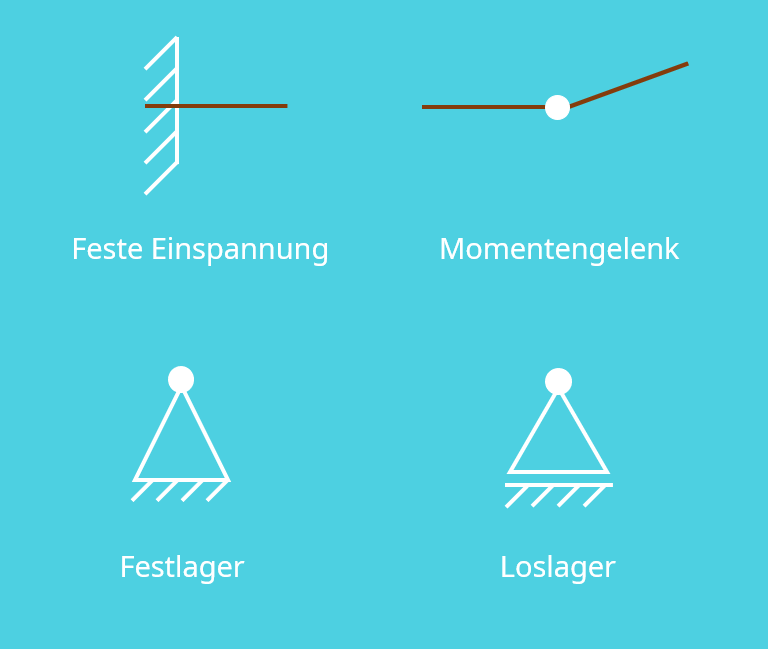
In der Statik gibt es insgesamt vier Arten von Lager. Dabei sind diese definiert als Orte, an denen der betrachtete Körper mit der Umgebung verbunden ist, und somit die Kräfte an die Umgebung übertragen werden. Die vier Arten sind die feste Einspannung, das Momentengelenk, das Festlager und das Loslager. Grafisch lassen sich diese wie folgt darstellen.
Im folgenden definieren wir jede Lagerart und erklären die Loslager Festlager Unterschiede.
Feste Einspannung
Bei der festen Einspannung handelt es sich um eine dreiwertige Lagerart, die Bewegungen in alle drei Koordinatenrichtungen unterbindet. Für die Definition der festen Einspannung kannst du dir einfach einen Stahlträger vorstellen. Dieser ist normalerweise fest mit einer Wand verbunden. Betrachten wir jetzt die Verbindung mit der Wand, finden wir dort die feste Einspannung. Bei dieser Art von Lagerung gibt es sechs verschiedene Auflagerreaktionen: Zum einen die Momente, bei denen wir im Räumlichen in jeder Koordinatenrichtung, also in 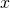 -,
-, 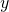 – und
– und  -Richtung, je eine haben. Auch bei den Kräften haben wir pro Koordinatenrichtung eine Kraft. Insgesamt ergeben sich somit also sechs Lagerreaktionen.
-Richtung, je eine haben. Auch bei den Kräften haben wir pro Koordinatenrichtung eine Kraft. Insgesamt ergeben sich somit also sechs Lagerreaktionen.
Momentengelenk
Weiter geht’s mit dem Momentengelenk. Dieses ist in der Regel einfach nur eine Verbindung zwischen zwei oder mehreren Körpern und sorgt dafür, dass zwischen den Körpern Kräfte aber keine Momente übertragen werden können. Das Momentengelenk ist damit schon etwas näher am Festlager und Loslager dran als die feste Einspannung. Stell dir als Beispiel ein einfaches Pendel vor: Das Pendel kann frei schwingen, obwohl du es an einem Punkt festhältst; dort befindet sich das Momentengelenk. Das Momentengelenk an sich, verursacht keine Auflagerreaktionen, sondern nur Zwischenreaktionen. Diese können einfach bestimmt werden:
Hierbei steht  für die Anzahl der Körper, die das Gelenk verbindet. Damit haben wir das Momentengelenk definiert und können uns jetzt den komplizierteren Fällen Loslager und Festlager widmen.
für die Anzahl der Körper, die das Gelenk verbindet. Damit haben wir das Momentengelenk definiert und können uns jetzt den komplizierteren Fällen Loslager und Festlager widmen.
Festlager
Als nächstes kommen wir zum Festlager. Dieses ist vom Prinzip eine Einspannung mit einem Momentengelenk. Dadurch wird kein Moment mehr übertragen, aber weiterhin Kräfte. Diese Lagerung kommt relativ häufig vor: Eine einfache Wippe stellt hier ein gutes Beispiel dar. Dabei befindet sich in der Mitte ein Festlager. Zählen wir nun die Auflagerreaktionen, kommen wir auf Kräfte in alle Richtungen des Koordinatensystems, aber auf keine Aufnahme von Momenten. Zusammengefasst ermöglicht also ein Festlager nur Drehungen im Lagerpunkt und erlaubt keine Verschiebungen. Deshalb wird auch von einem zweiwertigem Lager gesprochen. Es werden sowohl 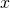 -, als auch
-, als auch 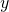 -Achsenbewegungen unterbunden.
-Achsenbewegungen unterbunden.
Loslager
Als letztes schauen wir uns noch das Loslager an. Hierbei handelt es sich um eine verschiebbare Lagerung eines Festlagers. Verglichen mit der Wippe heißt das nur, dass wir die Halterung der Wippe auf Rollen stellen. Aus diesem Grund heißt das Loslager auch Gleitlager oder verschiebliches Auflager. Diese Art des Lagers verhindert Bewegungen, die senkrecht zum Boden des Loslagers verlaufen. Aufgrund dessen wird von einem einwertigem Lager gesprochen. Somit nimmt es auch nur eine Kraft auf.
Loslager Festlager
Der Unterschied zwischen diesen beiden Lagerarten liegt in der Möglichkeit der Verschiebung. Das Festlager ermöglicht keine Verschiebungen. Bei einem Loslager hingegen kann in der Waagrechten verschoben werden. Des Weiteren ist das Loslager ein einwertiges und das Festlager ein zweiwertiges Lager. Ersteres ermöglicht mehr Bewegungen in verschiedene Richtungen als Letzteres.
Jetzt haben wir von „Kräfte aufnehmen“ gesprochen, da fragst du dich bestimmt was man darunter überhaupt versteht. In der Mechanik spricht man davon, wenn das jeweilige Lager einen Widerstand gegen die jeweilige Belastung aufbringen kann und im Umkehrschluss heißt es, dass es dann in die anderen Richtungen beweglich ist.
Loslager Festlager berechnen
Zur Berechnung von Los- und Festlagern ist es nötig, dass das zu berechnende System statisch bestimmt ist. Falls du genaueres zu der Definition und Erklärung der statischen Bestimmtheit wissen möchtest, haben wir dir hier unser Video dazu verlinkt.
Vereinfacht kann gesagt werden, dass wir im zweidimensionalen am Ende für drei unbekannte Lagerreaktionen nur drei Gleichungen aus den Freiheitsgraden bekommen. Und aus der Mathematik wissen wir, dass wir unser System dann einfach lösen können. Haben wir nun mehr Freiheitsgrade als Auflagerreaktionen, ist das System beweglich gelagert und wird „statisch unterbestimmt“ genannt.
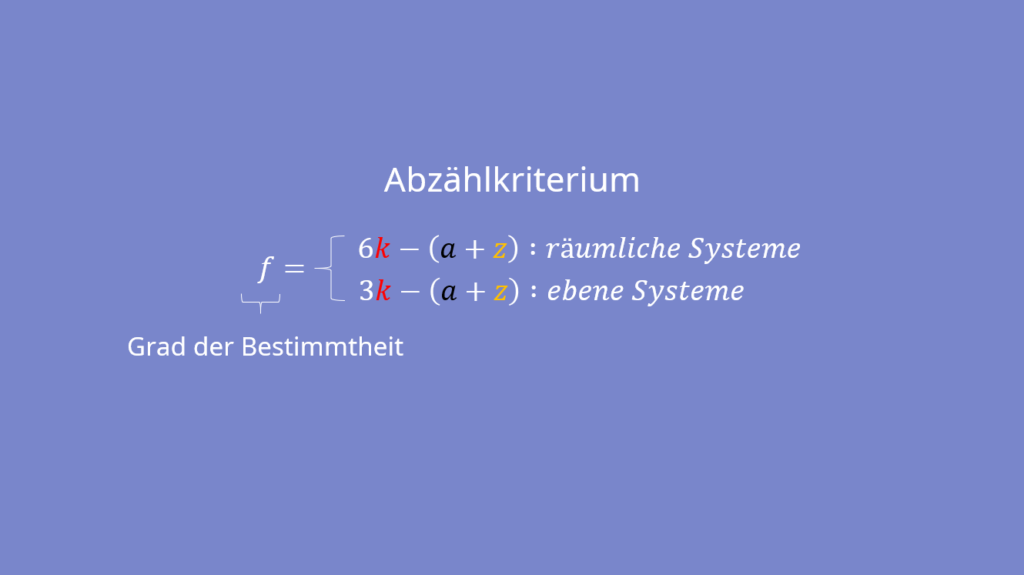
Um zu bestimmen, ob ein System statisch bestimmt ist, gibt es in der Statik das sogenannte Abzählkriterium. 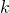 ist dabei die Anzahl der Körper,
ist dabei die Anzahl der Körper,  die Anzahl der Auflagerreaktionen und
die Anzahl der Auflagerreaktionen und  die Anzahl der Zwischenreaktionen.
die Anzahl der Zwischenreaktionen.
Hierbei ist 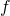 der Grad der Bestimmtheit. Sie kann wie folgt eingeteilt werden:
der Grad der Bestimmtheit. Sie kann wie folgt eingeteilt werden:
Ist 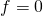 , dann ist das System statisch bestimmt.
, dann ist das System statisch bestimmt.
bei 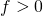 ist es
ist es 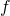 -fach verschiebbar.
-fach verschiebbar.
Ist  ist es
ist es 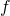 -fach statisch überbestimmt.
-fach statisch überbestimmt.
Doch uns interessieren hier erstmal nur die Systeme, die statisch bestimmt sind.
Statische Bestimmtheit Beispiel
Nehmen wir uns zur Ermittlung der statischen Bestimmtheit jetzt eine zweidimensionale Wippe als Beispiel. Die Anzahl der Körper ist dabei eins, sodass  gilt. Bei der Lagerung der Wippe handelt es sich um ein Festlager, weshalb wir Kräfte in jede Koordinatenrichtung haben. Somit ist
gilt. Bei der Lagerung der Wippe handelt es sich um ein Festlager, weshalb wir Kräfte in jede Koordinatenrichtung haben. Somit ist 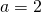 , da wir uns im zweidimensionalem befinden. Da wir nur einen Körper haben, gibt es keine Zwischenreaktionen und
, da wir uns im zweidimensionalem befinden. Da wir nur einen Körper haben, gibt es keine Zwischenreaktionen und 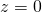 .
.
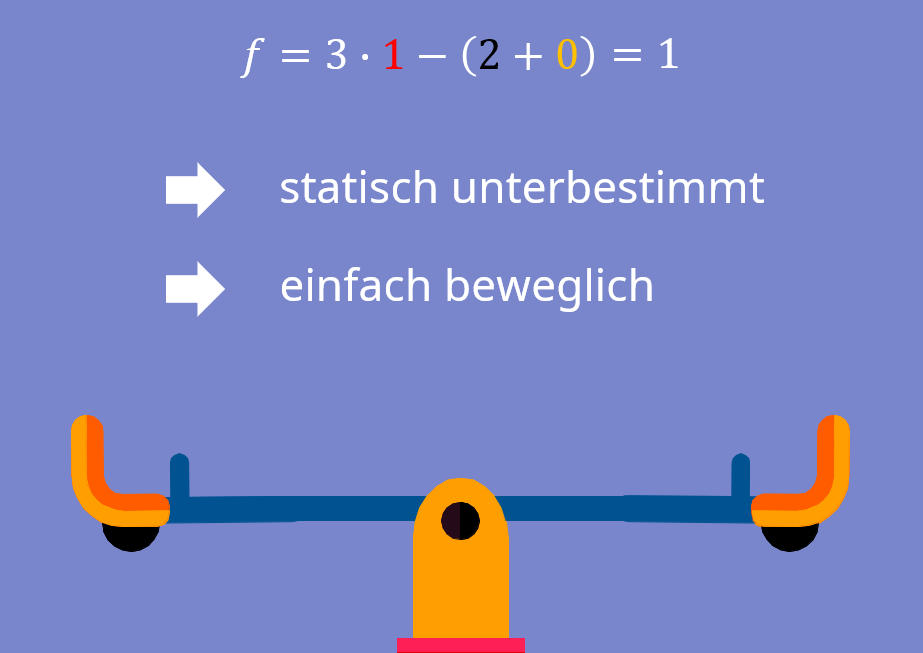
Eingesetzt in das Aufzählkriterium ergibt sich
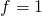
Das System ist somit statisch unterbestimmt.
Abschließend solltest du noch wissen, dass das Abzählkriterium nur eine notwendige, aber keine hinreichende Bedingung ist. Das heißt es gibt Systeme bei denen 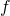 gleich
gleich 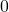 ist, aber das System trotzdem beweglich ist. Deshalb achte immer drauf ob nicht doch eine Bewegung möglich ist.
ist, aber das System trotzdem beweglich ist. Deshalb achte immer drauf ob nicht doch eine Bewegung möglich ist.