Ritterschnitt
Der Ritterschnitt oder auch das Ritterschnittverfahren wird häufig für Fachwerke im Bereich der Statik angewandt. In unserem Video erklären wir dir das Verfahren anhand eines Beispiels in nur 3 Minuten. Schau doch mal rein!
Inhaltsübersicht
Ritterschnitt einfach erklärt
Das Ritterschnittverfahren wird verwendet, um Stabkräfte in einem Fachwerk zu berechnen. Alle anderen Kräfte kannst du bei diesem Verfahren außer Acht lassen. Es werden die Stäbe so geschnitten, dass du genau drei Stabkräfte freistellst. Daraufhin kannst du dann Kräfte– beziehungsweise Momentengleichgewichte bilden.
Ritterschnittverfahren Beispiel
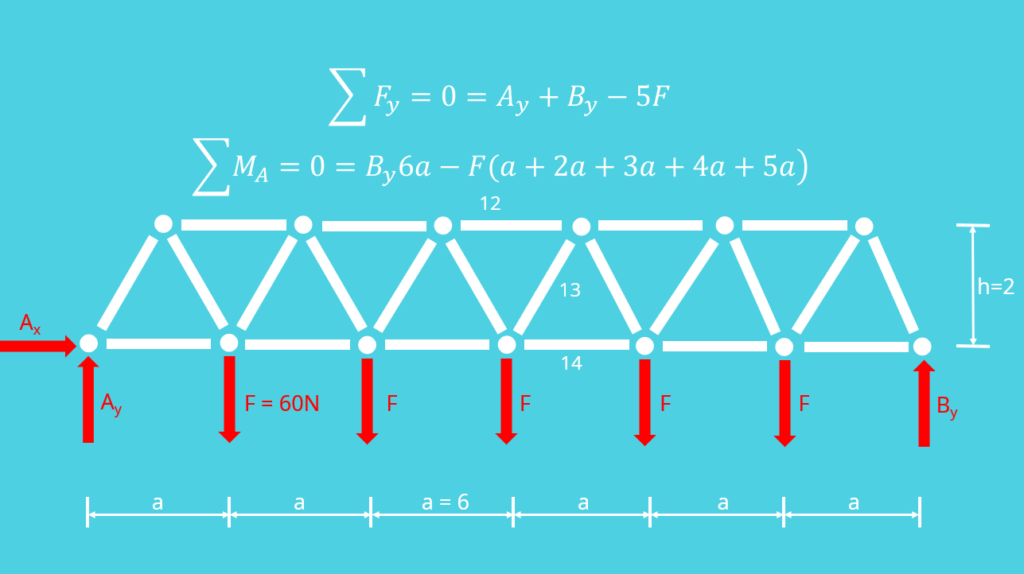
Damit du dir den Ritterschnitt gut vorstellen kannst, nehmen wir ein Fachwerk, das nach dem ersten Bildungsgesetz gebaut wurde. Die Bildungsgesetze kannst du in unserem Videobeitrag zu den Fachwerken, welchen wir dir hier
verlinkt haben, ansehen. Der horizontale Abstand der Knoten beträgt hier 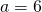 und die Höhe
und die Höhe 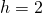 . Es wird durch ein Festlager
. Es wird durch ein Festlager 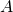 auf der linken Seite und ein Loslager
auf der linken Seite und ein Loslager 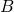 auf der rechten Seite befestigt. Die unterschiedlichen Lagerarten in der Statik findest du in diesem
Video erklärt. Das Fachwerk belasten wir dann mit fünf gleich starken Kräften von jeweils
auf der rechten Seite befestigt. Die unterschiedlichen Lagerarten in der Statik findest du in diesem
Video erklärt. Das Fachwerk belasten wir dann mit fünf gleich starken Kräften von jeweils 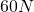 an den unteren Knoten.
an den unteren Knoten.
Rittersches Schnittverfahren Momentengleichgewicht
Für das Ritterschnittverfahren suchen wir zunächst die Kraft, die im Stab 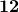 wirkt. Zu Beginn müssen wir wieder die Auflagerkräfte berechnen, indem wir ein Kräfte- und Momentengleichgewicht bilden. Falls du nicht mehr genau über die Gleichgewichtsbedingungen in der Statik bescheid weißt, kannst du in diesem
Video nachschauen.
wirkt. Zu Beginn müssen wir wieder die Auflagerkräfte berechnen, indem wir ein Kräfte- und Momentengleichgewicht bilden. Falls du nicht mehr genau über die Gleichgewichtsbedingungen in der Statik bescheid weißt, kannst du in diesem
Video nachschauen.
Als erstes formen wir das Momentengleichgewicht um das Festlager 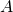 nach
nach 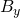 um und erhalten:
um und erhalten:
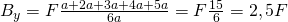
Daraus ergibt sich mit Hilfe des Kräftegleichgewichts:
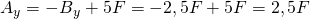
Somit haben beide Auflagerkräfte die gleiche Größe mit 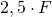 .
.
Als nächsten Schritt im Ritterschnitt schneiden wir durch die Stäbe 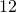 ,
, 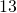 und
und 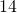 und betrachten die rechte Seite des Schnittes. Durch das Freischneiden erhalten wir die Stabkräfte
und betrachten die rechte Seite des Schnittes. Durch das Freischneiden erhalten wir die Stabkräfte 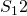 ,
, 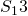 und
und 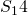 . Dann bilden wir das Momentengleichgewicht um einen Schnittpunkt der drei freigeschnittenen Kräfte. In unserem Fall nehmen wir den Schnittpunkt von
. Dann bilden wir das Momentengleichgewicht um einen Schnittpunkt der drei freigeschnittenen Kräfte. In unserem Fall nehmen wir den Schnittpunkt von 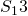 und
und 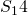 , die sich genau in einem Knoten schneiden. Das Momentengleichgewicht ergibt:
, die sich genau in einem Knoten schneiden. Das Momentengleichgewicht ergibt:
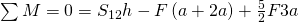
Nun müssen wir nur noch die Gleichung nach 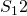 umstellen und erhalten:
umstellen und erhalten:
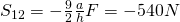
Wie du siehst, ist das Ritterschnittverfahren ganz einfach und wird dir von nun an keine Probleme mehr bereiten. Hiermit schlagen wir dich feierlich zum Ritterschnitt Experten!