Schnittgrößen
Die Begriffe Schnittgrößen, Streckenlast und Freischneiden lassen dir noch immer graue Haare wachsen? Dann kannst du dich jetzt entspannen, denn hier zeigen wir dir, dass das Thema rund um die Schnittgrößen gar nicht so schwierig ist.
Inhaltsübersicht
Schnittgrößen einfach erklärt
Zu Beginn ist es wichtig zu klären, was Schnittgrößen überhaupt sind. Man kann sie beschreiben als „innere Kräfte“ bzw. „innere Momente“, also auch Schnittkräfte oder Schnittmomente. Die Schnittkräfte können weiter in die Normalkraft und die Querkraft unterteilt werden. All diese Größen können durch einen senkrechten Schnitt „sichtbar“ werden. Der Schnitt wird aber natürlich nur gedanklich gemacht. Aus den Schnittgrößen lassen sich dann Spannungen ermitteln.
Schnittufer
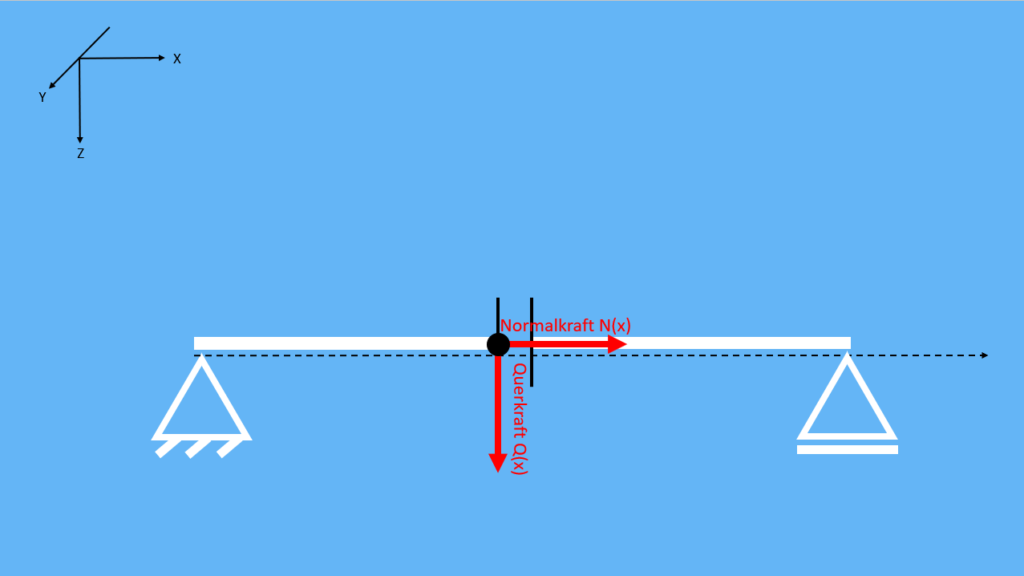
Betrachten wir vorerst für die Schnittkraftberechnung einen Balken unter ebener Belastung. Also wieder nur den zweidimensionalen Fall. Das Prinzip lässt sich aber auf das Räumliche ganz einfach erweitern.
Jetzt stellt sich die Frage, wie wir die Kraftrichtung annehmen. Dazu gibt es in der Mechanik wieder eine Konvention: das linke Schnittufer wird negatives Schnittufer und das rechte wird positives Schnittufer genannt. Positiv bzw. negativ heißt in diesem Fall einfach, dass Kräfte und Momente in positive bzw. negative Koordinatenrichtungen angenommen werden. Natürlich gibt es auch eine Konvention zur Ausrichtung des Koordinatensystems: Unter dem Balken wird eine „gestrichelte Faser“ angebracht. Sie zeigt an, dass die z-Achse nach unten zeigt. Die x-Achse zeigt immer durch den Balken hindurch und dementsprechend zeigt die y-Achse dann aus der Ebene heraus. Jetzt benennen wir noch die Kräfte: die Kraft in x-Richtung wird als Normalkraft 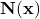 und die Kräfte in y- und z-Richtung werden als Querkraft
und die Kräfte in y- und z-Richtung werden als Querkraft 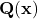 bezeichnet.
bezeichnet.
Schnittgrößen und Streckenlast
Als Streckenlast wird eine Kraft beschrieben, die sich über eine Strecke verteilt. Nun haben wir die Grundlagen zu Schnittgrößen, Streckenlast und Schnittufer geschaffen. Kommen wir nun zur Bestimmung von Schnittgrößen und der Streckenlast: Wie immer gehen wir von der Gleichgewichtsbedingung aus. Zuerst müssen wir die Auflagerkräfte berechnen, damit wir die vollständige Belastung des Balkens kennen. Danach schneiden wir den Balken an einer beliebigen Stelle  und bilden das Kräftegleichgewicht in x- und y-Richtung und das Momentengleichgewicht in z-Richtung in Abhängigkeit von
und bilden das Kräftegleichgewicht in x- und y-Richtung und das Momentengleichgewicht in z-Richtung in Abhängigkeit von  .
.
Falls du noch einmal nachschauen willst, was es mit den Gleichgewichtsbedingungen in der Statik auf sich hat, kannst du hier klicken. Für ein Beispiel zur Berechnung der Auflagerkräfte haben wir auch einen extra Videobeitrag.
Klingt alles ganz schön kompliziert, oder? Keine Sorge, folgendes Beispiel wird es dir deutlicher machen.
Schnittgrößen und Streckenlast Beispiel
Betrachten wir dazu einen einfachen Balken und schneiden ihn an einer beliebigen Stelle zwischen den Auflagern. Die Kräfte haben wir schon vorher bestimmt. Dann ergeben sich über die Gleichgewichtsbedingung folgende Gleichungen:
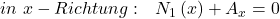
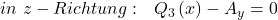
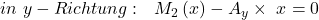
Wir sehen, dass in diesem Fall nur das Schnittmoment von  abhängig ist und die Quer- und Normalkraft über den Balken konstant sind.
abhängig ist und die Quer- und Normalkraft über den Balken konstant sind.
Schnittgrößen durch infinitesimale Betrachtung berechnen
Für einfache Anordnungen wie diese ist es ziemlich simpel die Schnittgrößen zu berechnen. Werden die Anordnungen aber komplizierter, ist die Berechnung deutlich aufwendiger. Deswegen verwenden wir wieder eine infinitesimale Betrachtung. Das ergibt einige differenzielle Zusammenhänge, die erstmal kompliziert wirken, unsere Arbeit jedoch erleichtern können:
Die Schnittgröße Schnittmoment wird durch ein 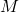 symbolisiert. Bei diesen Formeln bedeuten die kleinen Buchstaben, dass wir die Streckenlast betrachten. Dementsprechend können wir direkt jede Schnittgröße bestimmen, indem wir nur den jeweiligen Verlauf kennen und dann integrieren.
symbolisiert. Bei diesen Formeln bedeuten die kleinen Buchstaben, dass wir die Streckenlast betrachten. Dementsprechend können wir direkt jede Schnittgröße bestimmen, indem wir nur den jeweiligen Verlauf kennen und dann integrieren.
Streckenlast berechnen
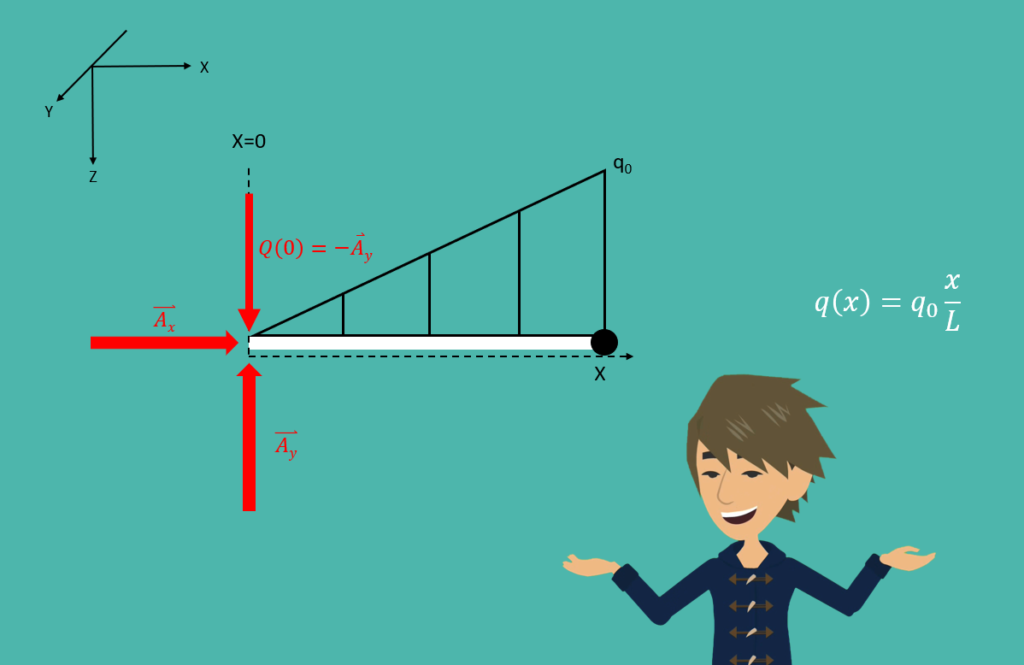
Das sieht jetzt natürlich wieder sehr aufwendig aus, ist aber gar nicht so schwer. Wir betrachten einfach wieder unseren Balken, nur diesmal unter einer dreieckigen Streckenlast.
Der Verlauf der Streckenlast ist damit:
Daraus ergibt sich dann durch einfaches integrieren der Querkraftverlauf:
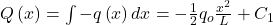
Die Konstante 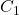 bestimmen wir einfach aus den Randbedingungen: z.B. muss an der Stelle
bestimmen wir einfach aus den Randbedingungen: z.B. muss an der Stelle 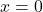 die Querkraft gleich der Auflagerkraft sein.
die Querkraft gleich der Auflagerkraft sein.
Für den Momentenverlauf gehen wir genauso vor. In diesem Fall haben wir keine Momentstreckenlast. Dementsprechend müssen wir hier nur den Querkraftverlauf integrieren:
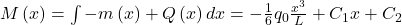
Für die Konstante 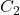 brauchen wir nun eine weitere Randbedingung: Da wir an der Stelle
brauchen wir nun eine weitere Randbedingung: Da wir an der Stelle 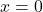 ein Momentengelenk haben, wissen wir, dass dort auch das Moment Null sein muss. Daraus folgt, dass
ein Momentengelenk haben, wissen wir, dass dort auch das Moment Null sein muss. Daraus folgt, dass 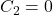 ist.
ist.
Nun haben wir die Schnittgrößen und die Streckenlast definiert und diese berechnet. Auch mit der integralen Berechnung des Querkraftverlaufs und Momentenverlaufs bist du jetzt vertraut. In einem zweiten Video, was wir dir hier verlinkt haben, gibt es eine Fortsetzung der Thematik Schnittgrößen. Dabei schauen wir uns das Vorgehen zur Berechnung der Größen anhand eines Beispiels an. Falls du lieber den Text lesen möchtest, findest du diesen hier im Anschluss.
Schnittgrößen und Freischneiden
Um die Schnittgrößen für ein beliebiges System zu berechnen, kannst du wie folgt vorgehen:
Zuerst musst du das System freischneiden, dann die Auflagerkräfte berechnen und als letztes die Schnittgrößen über die Gleichgewichtsbedingungen bestimmen.
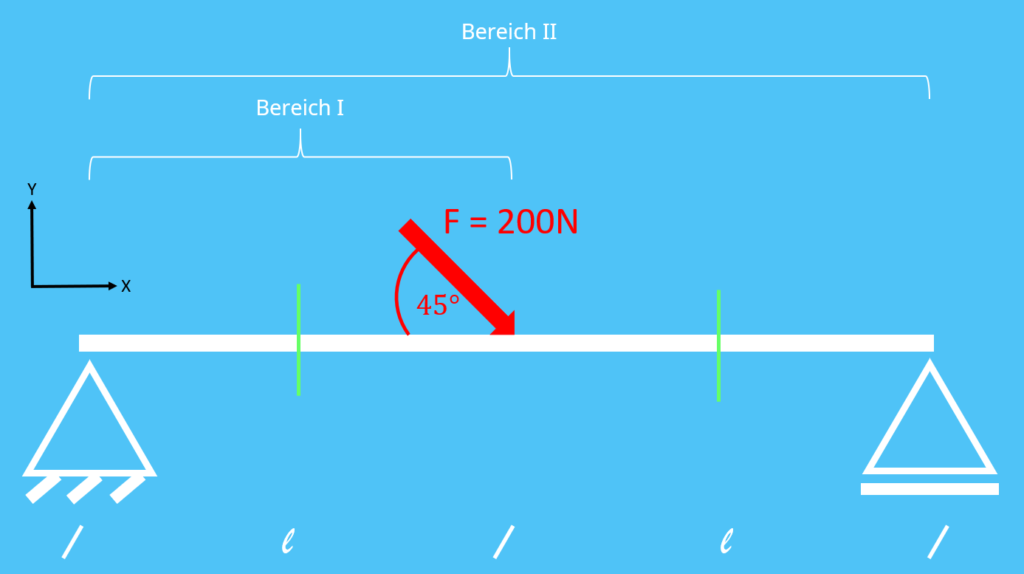
In unserem Fall sieht das System so aus:
Wie du siehst haben wir einen ebenen Balken, der mit einem Festlager und einem Loslager befestigt ist und auf den zusätzlich eine Kraft von 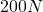 in einem Winkel von
in einem Winkel von 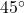 wirkt.
wirkt.
Freischneiden
Für das Freischneiden gibt es wieder eine Konvention. Wirkt auf den Balken zusätzlich zu den Lagerkräften eine Kraft, dann wird direkt vor und direkt hinter dieser Kraft geschnitten, der sogenannte Freischnitt. Das bedeutet, dass der erste Bereich unmittelbar vor der Kraft endet. Zur Visualisierung zeichnet man die Schnitte allerdings nicht direkt bei der Kraft ein. Der zweite Bereich umfasst den gesamten Balken. Nun haben wir unsere zwei Bereiche und können die Auflagerkräfte bestimmen.
Dafür muss man wissen, dass uns ein Festlager immer eine Kraft in horizontaler und eine in vertikaler Richtung liefert. Das Loslager hingegen bringt uns nur eine Kraft in vertikaler Richtung hervor. Jetzt haben wir alle Kräfte eingezeichnet und können uns mit Hilfe der Gleichgewichtsbedingungen an die Berechnung der Auflagerkräfte machen.
Auflagerkräfte berechnen
Das Vorgehen ist hier immer gleich: zuerst stellen wir in jede Richtung unsere Kräfte– und Momentengleichgewichte auf.
Als erstes betrachten wir die horizontale Richtung. In unserem Beispiel wirken hier die Kraft 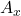 und die Kraft
und die Kraft 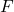 . Da die Kraft
. Da die Kraft 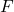 schräg auf den Balken auftrifft, wirkt sie nur zu einem Teil in x-Richtung. Nämlich nur mit dem Anteil
schräg auf den Balken auftrifft, wirkt sie nur zu einem Teil in x-Richtung. Nämlich nur mit dem Anteil 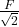 . Dies ergibt sich aus den trigonometrischen Beziehungen. Für unser Gleichgewicht in x-Richtung gilt also:
. Dies ergibt sich aus den trigonometrischen Beziehungen. Für unser Gleichgewicht in x-Richtung gilt also:
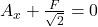
Wir stellen die Formel nun nach 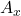 um und setzen für
um und setzen für  ein. Dadurch ergibt sich für
ein. Dadurch ergibt sich für 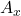 eine Kraft von
eine Kraft von 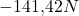 .
.
Die vertikalen Kräfte sind in unserem Beispiel die Kraft 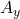 , die entlang der y-Achse wirkt, die Kraft
, die entlang der y-Achse wirkt, die Kraft 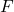 , die anteilig entgegen wirkt und die Kraft
, die anteilig entgegen wirkt und die Kraft 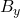 , die wiederum entlang der y-Achse wirkt. Als Formel ausgedrückt sieht das dann so aus:
, die wiederum entlang der y-Achse wirkt. Als Formel ausgedrückt sieht das dann so aus:
Wenn wir diese Formel nun nach 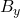 umstellen, fällt auf, dass wir zwei Unbekannte haben –
umstellen, fällt auf, dass wir zwei Unbekannte haben – 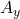 und
und 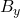 . Wir müssen also zuerst an einer anderen Stelle weitermachen, um
. Wir müssen also zuerst an einer anderen Stelle weitermachen, um 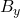 ausrechnen zu können.
ausrechnen zu können.
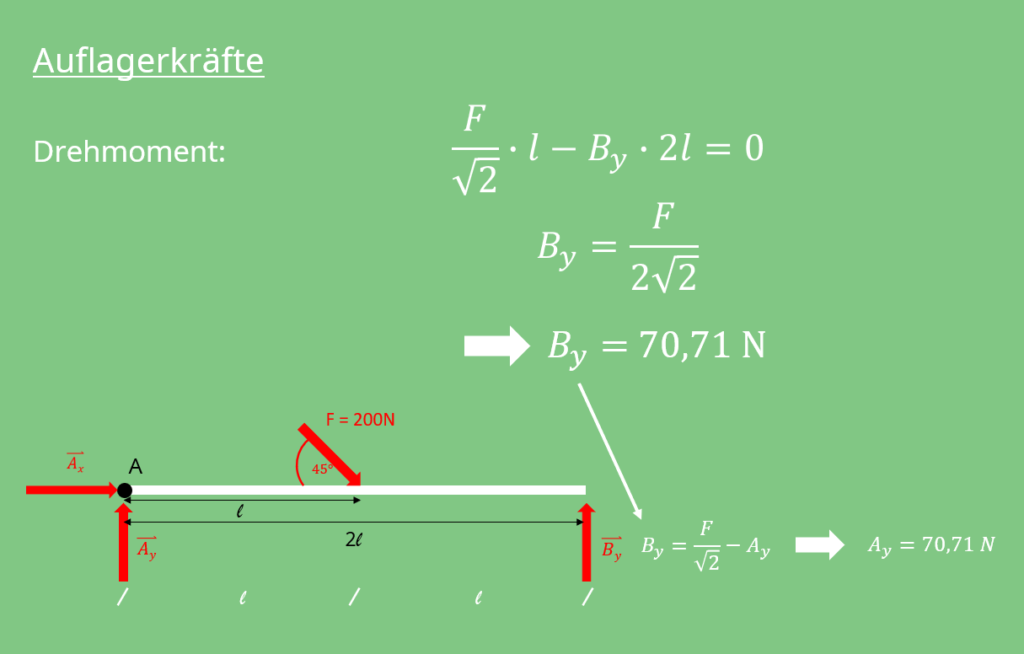
Drehmoment berechnen
Hier bietet sich das Drehmoment
an. Wir legen fest, dass wir den Punkt 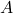 betrachten und unser Moment im Uhrzeigersinn drehen lassen. Rotieren wir nun rechts um den Punkt
betrachten und unser Moment im Uhrzeigersinn drehen lassen. Rotieren wir nun rechts um den Punkt 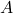 herum, stellen wir fest, dass die Kraft
herum, stellen wir fest, dass die Kraft 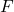 anteilig positiv zur Drehung beiträgt und, dass die Kraft
anteilig positiv zur Drehung beiträgt und, dass die Kraft 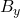 dieser entgegenwirkt. Da es sich hier um Drehmomente handelt, ist es wichtig, dass du den Abstand zu unserem Drehpunkt nicht vernachlässigst. Die Formel sieht dann so aus:
dieser entgegenwirkt. Da es sich hier um Drehmomente handelt, ist es wichtig, dass du den Abstand zu unserem Drehpunkt nicht vernachlässigst. Die Formel sieht dann so aus:
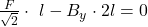
Jetzt können wir die Formel nach 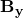 umstellen und erhalten dann nach Einsetzen unserer Zahlen eine Kraft
umstellen und erhalten dann nach Einsetzen unserer Zahlen eine Kraft 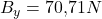 . Du siehst, dass wir nun auch unsere Kraft
. Du siehst, dass wir nun auch unsere Kraft 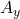 ausrechnen können, indem wir
ausrechnen können, indem wir 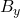 in die vorherige Formel einsetzen. Daraus ergibt sich eine Kraft
in die vorherige Formel einsetzen. Daraus ergibt sich eine Kraft 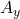 von
von 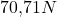 .
.
Jetzt haben wir alle Auflagerkräfte bestimmt und können uns endlich an die Berechnung der Schnittgrößen machen.
Berechnung der Schnittgrößen
Hier muss man jeden Bereich separat betrachten. Im ersten Bereich wirkt in horizontaler Richtung nun zusätzlich zu den bekannten Kräften noch die Normalkraft 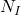 . Die Kraft
. Die Kraft 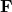 ist hier nicht relevant, da wir ja vor der Kraft geschnitten haben. Daraus resultiert folgende Formel:
ist hier nicht relevant, da wir ja vor der Kraft geschnitten haben. Daraus resultiert folgende Formel:
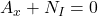
Wenn wir die Formel umstellen, dann gilt für unsere Schnittgröße:
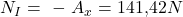
Für die vertikale Richtung im ersten Bereich erfolgt die Rechnung analog. Hier wirkt die Querkraft 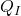 der Kraft
der Kraft 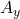 entgegen, die Kraft
entgegen, die Kraft 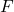 bleibt wieder unbeachtet. Für
bleibt wieder unbeachtet. Für 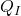 ergibt sich dann ein Wert von
ergibt sich dann ein Wert von 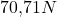 .
.
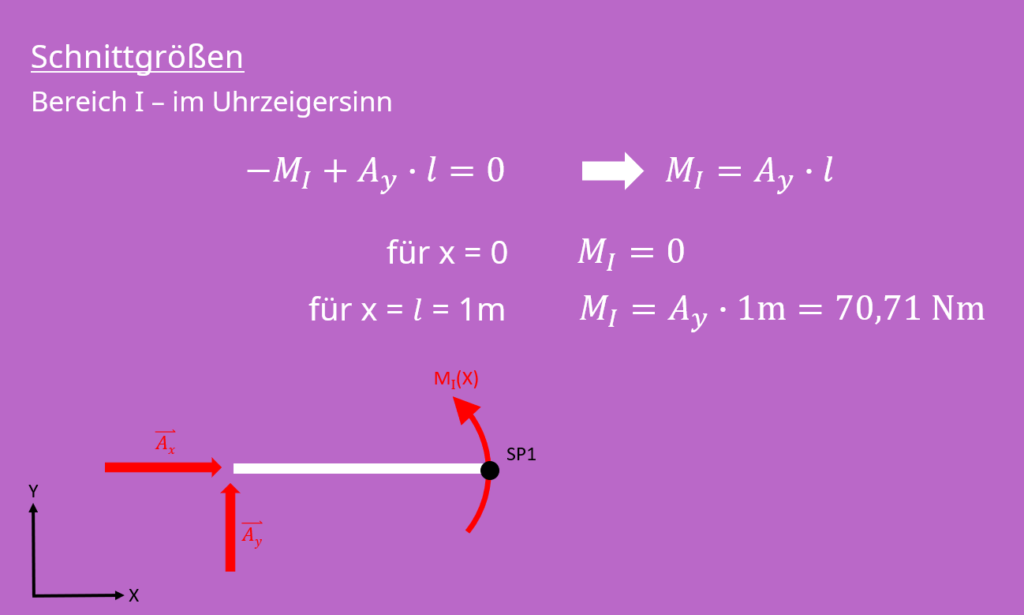
Schnittmoment bestimmen
Nun bestimmen wir das Schnittmoment. Wir drehen im Uhrzeigersinn um unseren Schnittpunkt 1. Das Moment 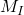 wirkt unserer Drehung also entgegen und die Kraft
wirkt unserer Drehung also entgegen und die Kraft 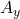 begünstigt unsere Drehung. Wichtig ist, dass wir wieder den Abstand zum Drehpunkt betrachten. Das ergibt dann:
begünstigt unsere Drehung. Wichtig ist, dass wir wieder den Abstand zum Drehpunkt betrachten. Das ergibt dann:
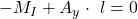
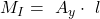
Du siehst, dass unser Drehmoment an der Stelle 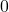 gleich
gleich 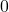 ist und bei „L ist gleich ein Meter“ den Wert
ist und bei „L ist gleich ein Meter“ den Wert 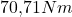 annimmt.
annimmt.
Als nächstes bestimmen wir die Schnittgrößen für den zweiten Bereich. Die Berechnung erfolgt analog zu Bereich I, allerdings kommt jetzt noch die Kraft 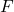 und die Auflagerkraft
und die Auflagerkraft 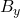 hinzu.
hinzu.
In horizontaler Richtung wirkt die Kraft 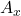 , die Normalkraft
, die Normalkraft 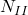 und anteilig die Kraft
und anteilig die Kraft 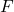 . Nach Umstellen und Einsetzen erhalten wir
. Nach Umstellen und Einsetzen erhalten wir 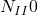 .
.
In y-Richtung sieht das sehr ähnlich aus. Hier wirkt die Kraft 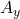 der Kraft
der Kraft 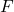 und der Querkraft
und der Querkraft 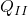 entgegen. In Formeln kann man das folgendermaßen ausdrücken:
entgegen. In Formeln kann man das folgendermaßen ausdrücken:
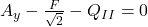
und
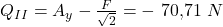
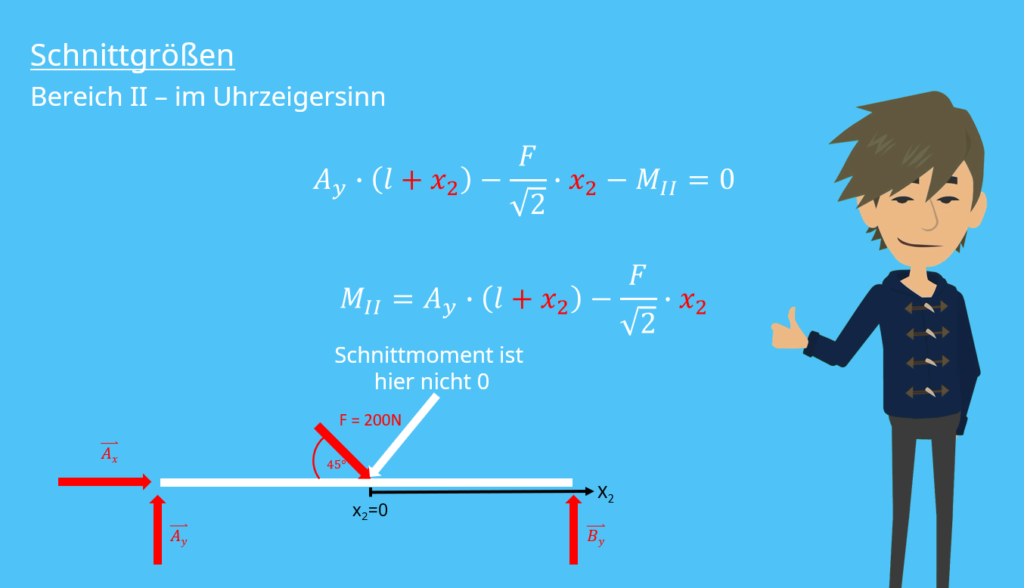
Jetzt fehlt nur noch das Schnittmoment für den zweiten Bereich. Wir müssen wieder das Schnittmoment für beide Enden unseres Bereichs bestimmen, allerdings ist unser Moment am positiven Schnittufer nicht wie vorher Null. Wir führen deswegen die Laufvariable 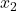 ein.
ein. 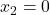 befindet sich dann direkt am Punkt der Krafteinwirkung von
befindet sich dann direkt am Punkt der Krafteinwirkung von 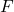 . Unsere Formel sieht nun ein kleines bisschen anders aus:
. Unsere Formel sieht nun ein kleines bisschen anders aus:
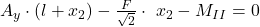
und
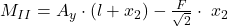
Setzen wir nun unsere Angaben ein. Für 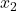 nehmen wir
nehmen wir 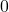 an. Daraus folgt:
an. Daraus folgt:
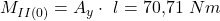
Und um das Drehmoment am Ende unseres Balkens herauszufinden, setzen wir nun für 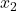
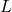 ein.
ein.
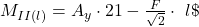 ≈ 0 Nm
≈ 0 Nm
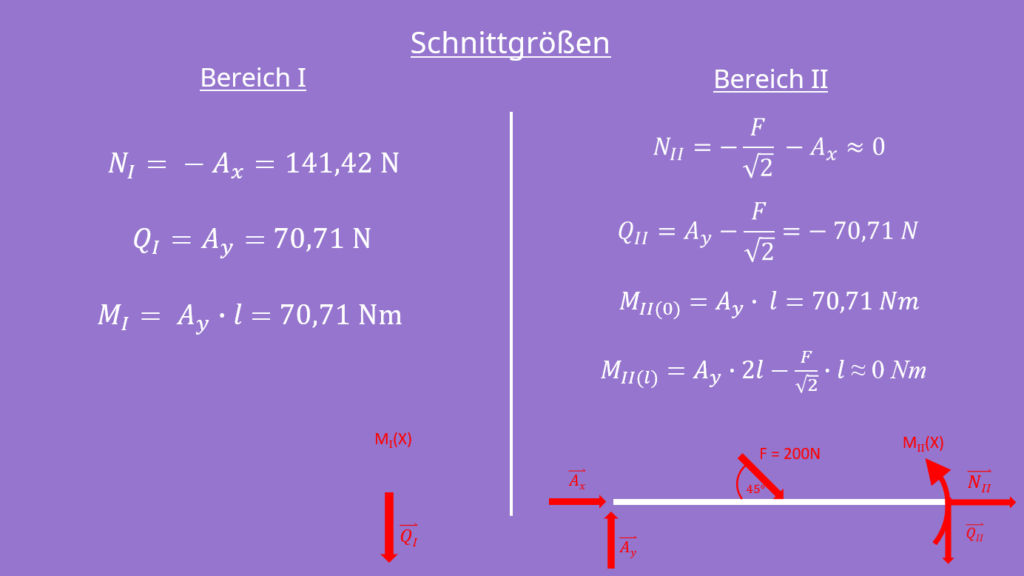
So kannst du ganz einfach die Schnittgrößen für jeden beliebigen Balken ausrechnen. Hier hast du nochmal alle Schnittgrößen für unser System im Überblick:
Ab sofort kannst du nun mit deinem Wissen über Schnittgrößen, Streckenlast und Freischneiden glänzen.