Steigungswiderstand & Beschleunigungswiderstand
In diesem Artikel betrachten wir zwei Fahrwiderstände: den Steigungswiderstand und den Beschleunigungswiderstand. Du lernst, wodurch sie entstehen und wie sie berechnet werden.
Inhaltsübersicht
Herleitung des Steigungswiderstands und des Beschleunigungswiederstands
Beginnen wir mit dem Steigungswiderstand! Jeder kennt es: Fahren wir mit einem Auto einen Berg hinauf, dann werden wir entweder langsamer oder müssen mehr Gas geben, um die Geschwindigkeit halten zu können. Verantwortlich dafür ist der Steigungswiderstand. Dieser ist einerseits abhängig von der Fahrzeugmasse und andererseits vom Steigungswinkel. Daraus folgt:

Eine Steigung liegt bei einem positiven Winkel α, bei einem negativen Winkel α sprechen wir von einem Gefälle. Bei Steigungen tritt die Kraft als Widerstandskraft auf, bei Gefällen als Hangabtriebskraft.
Berechnung des Steigungswiederstands mit Hilfe der Dreiecksformel
Wenn du schonmal in der Bergen unterwegs warst, dann ist dir bestimmt aufgefallen, dass die Steigung oft auf einem Verkehrsschild in Prozent angegeben ist. Diese Prozentzahl lässt sich mit dem Tangens aus dem Winkel  berechnen. Auch daraus können wir den Steigungswiderstand berechnen:
berechnen. Auch daraus können wir den Steigungswiderstand berechnen:
![Rendered by QuickLaTeX.com F_{St}=m\ \ast \ g\ \ast \tan\ ( \frac{p[\%]}{100} )](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-9e03931e1bc31f459559adf9358afd11_l3.png)
Da für kleine Winkel der Tangens ungefähr gleich dem Sinus entspricht und dieser wiederum dem Wert des Winkels selbst, können wir näherungsweise vereinfachen zu:
Jetzt wissen wir, was es mit dem Steigungswiderstand auf sich hat und können uns dem Beschleunigungswiderstand widmen. Dieser tritt bei der Beschleunigung von trägen Massen auf und wirkt der Bewegungsrichtung entgegen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Der Beschleunigungswiderstand
Um den Beschleunigungswiderstand zu erhalten, addierst du einfach die translatorische und die rotatorische Widerstandskraft:

Wollen wir den Beschleunigungswiderstand in Abhängigkeit der translatorischen Beschleunigung 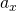 ausdrücken, müssen wir die Gleichung weiter auflösen.
ausdrücken, müssen wir die Gleichung weiter auflösen.
Der Translatorische Widerstand
Der translatorische Widerstand setzt sich aus der Masse des Fahrzeugs und der translatorischen Beschleunigung des Fahrzeugs zusammen. Hier gilt:

Der Rotatorischer Widerstand
Die rotatorische Widerstandskraft bezieht sich auf die Beschleunigung des Rads. Für sie gilt:

Dabei entspricht  dem Radius des Rades und
dem Radius des Rades und  dem Rotationsmoment. Letzteres erhalten wir indem wir das Trägheitsmoment des Reifens
dem Rotationsmoment. Letzteres erhalten wir indem wir das Trägheitsmoment des Reifens  mit der rotatorischen Winkelbeschleunigung
mit der rotatorischen Winkelbeschleunigung  multiplizieren:
multiplizieren:

Unter Vernachlässigung des Schlupfs können wir die Winkelbeschleunigung wie folgt ausdrücken:

 ist dabei die translatorische Beschleunigung und
ist dabei die translatorische Beschleunigung und  der Radius des Reifens. Damit ergibt sich für die rotatorische Widerstandskraft:
der Radius des Reifens. Damit ergibt sich für die rotatorische Widerstandskraft:

Sie ist also ungefähr gleich dem Trägheitsmoment geteilt durch den Radius des Reifens zum Quadrat mal der translatorischen Beschleunigung.
Der Beschleunigungswiderstand in Abhängigkeit von 
Jetzt können wir den Beschleunigungswiderstand als Funktion der translatorischen Beschleunigung formulieren:
Wenn du diese Formeln kombinierst und vereinfachst kommst du auf eine neue Formel die du jetzt immer zur Berechnung des Beschleunigungswiderstands verwenden kannst: 
Zusammenfassung
Fassen wir zusammen: der Steigungswiderstand tritt, wie der Name schon sagt, bei einer Steigung auf. Bei einem Gefälle wirkt dagegen die Hangabtriebskraft. Der Beschleunigungswiderstand entsteht bei der Beschleunigung von trägen Massen. Er setzt sich aus dem rotatorischen und translatorischen Widerständen zusammen.

