Einspurmodell
Das Einspurmodell ist ein vereinfachtes Modell zur Beschreibung der Querdynamik eines Fahrzeugs. In diesem Beitrag schauen wir uns an, was es damit auf sich hat.
Inhaltsübersicht
Querkräfte
Wenn wir das Fahrzeug in Querrichtung bewegen – beispielsweise bei einer Kurvenfahrt – dann geben wir über das Lenkrad einen Lenkimpuls. Durch diesen werden die Vorderräder schräg zur Längsachse ausgerichtet. Fahren wir langsam, dann wirken keine Querkräfte. Bei schnellen Kurvenfahrten erzeugen die Vorderräder durch den Lenkwinkel Seitenkräfte. Diese beschleunigen das Fahrzeug in Querrichtung.
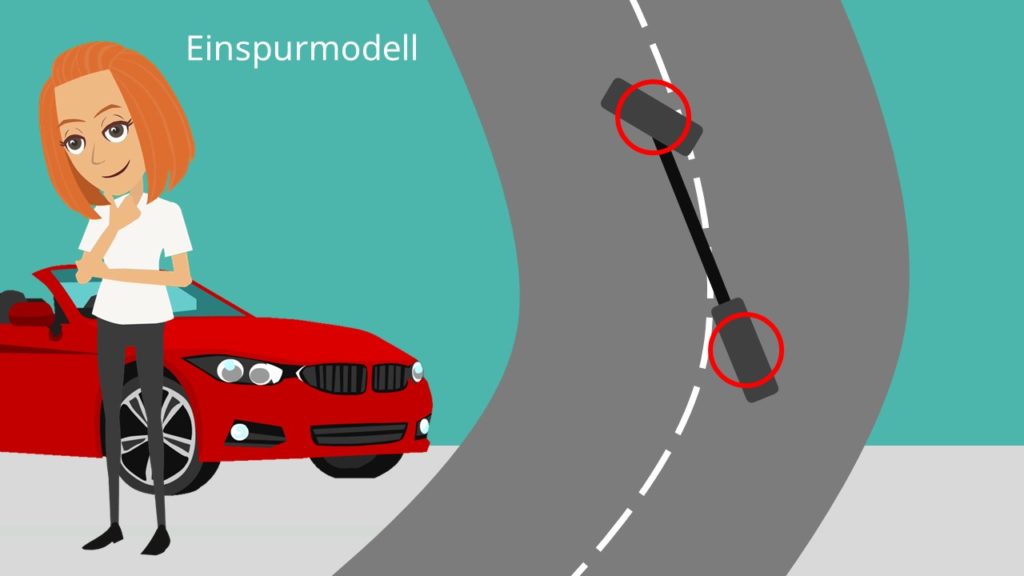
Eine Berechnung der Querkräfte für das ganze Fahrzeug ist recht aufwendig. Daher wird das Fahrzeugmodell vereinfacht: Wir nehmen an, dass der Schwerpunkt des Fahrzeugs auf Fahrbahnhöhe liegt. Dadurch kann es nicht zu Wank- und Hubbewegungen kommen. Des Weiteren führen wir die beiden Räder einer Achse zu einem Rad in der Fahrzeugmitte zusammen.
Betrachten wir das Modell, dann sehen wir, dass das Fahrzeug nur noch aus einem Hinter- und einem Vorderrad besteht. Die Räder haben jedoch jeweils die Eigenschaften beider Räder der jeweiligen Achse.
Wenn wir schnell durch eine Kurve fahren, dann zeigt die Längsachse des Fahrzeugs nicht in die Richtung des Geschwindigkeitsvektors. Die Abweichung wird mit dem Schwimmwinkel  angegeben. Die Abweichung der Längsachse zur festen x-Achse wird mit dem Gierwinkel
angegeben. Die Abweichung der Längsachse zur festen x-Achse wird mit dem Gierwinkel  beschrieben. Beim Einlenken des Rads stellt sich der Lenkwinkel
beschrieben. Beim Einlenken des Rads stellt sich der Lenkwinkel  zwischen dem Rad und der Längsachse ein. Für eine seitenkraftfreie Kurvenfahrt wird dieser auch als Ackermannlenkwinkel bezeichnet. Die Bewegung des Fahrzeugs lässt sich durch die translatorische Schwerpunktgeschwindigkeit und die rotatorische Giergeschwindigkeit um die z-Achse beschreiben.
zwischen dem Rad und der Längsachse ein. Für eine seitenkraftfreie Kurvenfahrt wird dieser auch als Ackermannlenkwinkel bezeichnet. Die Bewegung des Fahrzeugs lässt sich durch die translatorische Schwerpunktgeschwindigkeit und die rotatorische Giergeschwindigkeit um die z-Achse beschreiben.
Seitenführungskraft
Wie entstehen nun die Seitenkräfte? Durchfahren wir eine Kurve, dann entsteht durch die Zentripetalbeschleunigung eine Seitenkraft. Sie erhältst du, indem du die Fahrzeuggeschwindigkeit zum Quadrat durch den Kurvenradius teilst und mit der Fahrzeugmasse multiplizierst:

Die Seitenkraft wird nach dem Prinzip von d’Alembert als Trägheitskraft betrachtet. Falls du noch nicht weißt, was es mit diesem Prinzip auf sich hat, schaue dir doch gern unser Video dazu an.
Die Trägheitskraft ist der Beschleunigung des Fahrzeugs entgegengesetzt. Wenn wir uns in einem Auto befinden, das schnell durch eine Kurve fährt, dann spüren wir diese, weil wir nach außen gedrückt werden. Um der Kraft entgegenzuwirken, wirken an dem Vorder- und Hinterrad Seitenführungskräfte, die das Fahrzeug auf der Kreisbahn halten. Diese können wir durch folgende Formeln berechnen:


Die Seitenkräfte an den Reifen können nur erzeugt werden, wenn sie mit einem Schräglaufwinkel abrollen. Das heißt, dass die Längsachse des Rades versetzt zu seinem Geschwindigkeitsvektor stehen muss. Es stellt sich jeweils ein Schräglaufwinkel für das Vorderrad und einer für das Hinterrad ein. Berechnen lassen sich die Schräglaufwinkel wie folgt:


Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Bewegungsgleichungen
Als nächstes wollen wir die Bewegungsgleichungen für das Fahrzeug unter Berücksichtigung der Umfangskräfte untersuchen. Du kannst dir zur Wiederholung unser Video zum Fahrzeugkoordinatensystem anschauen. Für die Kräftegleichgewichte in Längs- und Querrichtung gelten die folgenden Formeln:
Auf der linken Seite finden wir jeweils die Beschleunigungskräfte in x- beziehungsweise Längsrichtung und y- beziehungsweise Querrichtung. Die Terme auf der rechten Seite sehen sehr ähnlich aus. Wir müssen hier den Lenkwinkel  , die Umfangskraft vorne
, die Umfangskraft vorne  und die Seitenführungskraft vorne berücksichtigen
und die Seitenführungskraft vorne berücksichtigen  . Während für die Gleichung in x-Richtung noch die Umfangskraft hinten
. Während für die Gleichung in x-Richtung noch die Umfangskraft hinten  berücksichtigt wird, ist dies bei der zweiten Gleichung die Seitenführungskraft hinten
berücksichtigt wird, ist dies bei der zweiten Gleichung die Seitenführungskraft hinten  .
.
Außerdem liegt noch eine Gierbewegung des Fahrzeugs um die z-Achse vor. Diese können wir mit dem Momentengleichgewicht um den Schwerpunkt beschreiben:

Beschleunigungen im Einspurmodell
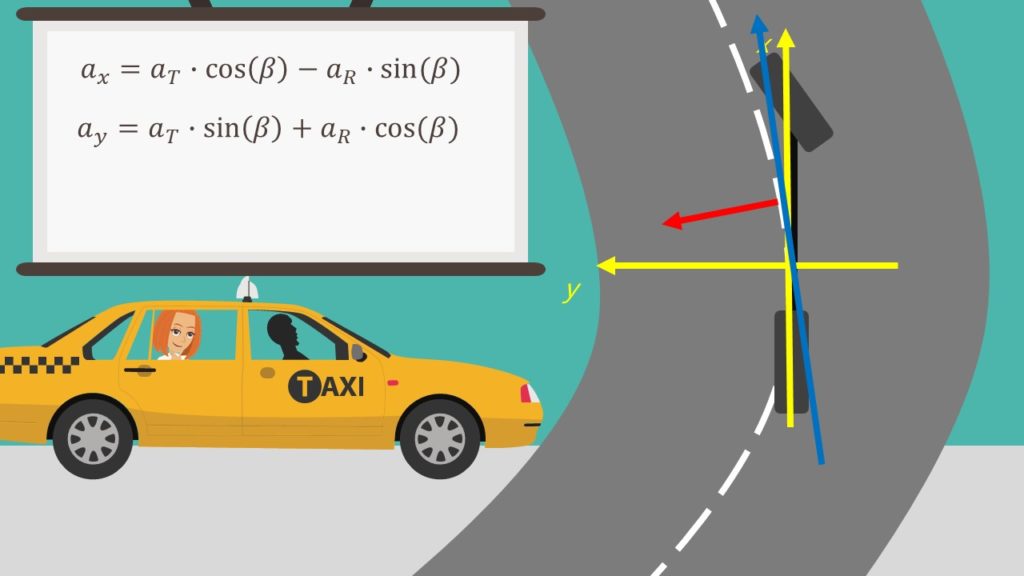
Wenn wir in einem Fahrzeug sitzen, interessieren uns die wirkenden Beschleunigungen des Fahrzeugs allerdings mehr als die Kräfte. Aus diesem Grund schauen wir uns den Zusammenhang zwischen den Beschleunigungen einmal näher an. Sie können mit der Radial- und Tangentialbeschleunigung beschrieben werden. Die Radialbeschleunigung wirkt zum Kurvenmittelpunkt und die Tangentialbeschleunigung wirkt tangential zur Kreisbahn. Dadurch ergeben sich für die Längs- und Querbeschleunigung folgende Formeln:
Wir müssen sowohl für die Längsbeschleunigung  als auch für die Querbeschleunigung
als auch für die Querbeschleunigung  dieselben Größen beachten: Die Tangentialbeschleunigung
dieselben Größen beachten: Die Tangentialbeschleunigung  , die Radialbeschleunigung
, die Radialbeschleunigung
 und den Schwimmwinkel
und den Schwimmwinkel  .
.
Wenn wir nun für die Radial-, die Zentripetalbeschleunigung einsetzen und für die Tangential- die Fahrzeugbeschleunigung, dann erhalten wir:


Mit diesen Formeln kannst du nun recht einfach die Beschleunigungen berechnen.
Sehr gut! Fassen wir zusammen, was wir in diesem Beitrag gelernt haben! Das Einspurmodell ist ein vereinfachtes Fahrzeugmodell zur Beschreibung der Querkräfte. Bei Kurvenfahrten wirken auf die Reifen Seitenführungskräfte, die der Zentripetalkraft entgegenwirken.