Bindungsenergie
Was die Bindungsenergie ausmacht und wie du sie berechnest, das erfährst du hier.
Schau auf jeden Fall noch das Video zum Artikel. Darin sind alle relevanten Inhalte für dich bereits audiovisuell aufbereitet.
Inhaltsübersicht
Was ist Bindungsenergie?
Bei der Bindungsenergie handelt es sich um die geringste, notwendige Energie , die du brauchst um ein gebundenes System aus zwei oder mehr Teilchen in seine Bestandteile zu zerlegen. Die Bindungsenergie steckt allerdings nicht im System selbst, sondern wurde bereits bei dessen Bildung frei gesetzt. Binden sich zwei oder mehr Teilchen aneinander setzen diese eine Energie frei, die dem Energiebetrag entspricht, welchen du aufwenden musst, um das System zu zerlegen.
Bei der Bindungsenergie handelt es sich nicht um eine im System enthaltene Energie, sondern um die Energie die bei der Zusammensetzung des Systems abgegeben wurde. Das wird vor allem in der Chemie näher betrachtet. Hier bezeichnet die Bindungsenergie die Änderung des Energiegehalts des Systems bei der Verbindung seiner Teile. Der Energiebetrag ist der gleiche, jedoch ist das Vorzeichen negativ.
In der Kernphysik betrachtest du die Bindungsenergie zwischen den Nukleonen des Kerns und in der Teilchenphysik die Bindungsenergie des gesamten Atoms mit Elektronen.
Bindungsenergie Formel
Zur besseren Veranschaulichung, stell dir zwei Dauermagneten vor, welche durch ihre Anziehung aufeinander zu fliegen. Kurz bevor sich die beiden Magneten treffen, ist ihre kinetische Energie am größten. Bei Kontakt setzen beide Magneten die Bindungsenergie in Form von Schallwellen und Wärme frei. Um beide Magneten wieder voneinander zu trennen, musst du den gleichen Energiebetrag aufwenden der auch freigesetzt wurde.
Es ist dir möglich dies mathematisch zu beschreiben. Du stellst jedoch fest, dass deine Formel für verschiedene Fachbereiche verschieden aussieht. Grundsätzlich hat sie aber immer die gleiche Struktur.
Diese Formel kommt aus der Relativitätstheorie.
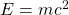
In dieser Formel ist 
die Energie, 
die Masse und 
die Lichtgeschwindigkeit
. Betrachtest du ein aus Teilchen zusammengesetztes System, stellst du fest, dass dessen Masse geringer ist, als die Summe der Massen seiner Bestandteile. Diese Massendifferenz, auch Massendefekt
, 
ist, wie du an Einsteins Formel erkennst, Äquivalent zu einem Energiebetrag.
Hier steht 
für die Bindungsenergie.
Atomphysik
In der Atomphysik bezeichnet die Bindungsenergie, die Energie die du benötigst um ein Atom in ein anderes Atom und ein Elektron zu zerlegen.
In der Formel bezeichnet 
die Bindungsenergie aller Elektronen der Atomhülle.
Hier steht 
für die Kernmasse des Atoms, 
für dessen Ordnungszahl, 
für die Masse des Elektrons,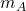 
für die Masse des Atoms und für die Lichtgeschwindigkeit.
Im Experiment ist es schwer die gesamte Bindungsenergie eines Atoms zu messen. In der Regel benutzt du hierzu meist theoretische Ansätze.
Kernphysik
Stell dir vor du hast die Bausteine eines Atomkerns vor dir. Also eine Menge an Protonen und Neutronen. Alle diese Teilchen liegen soweit voneinander entfernt, dass keine Kräfte zwischen ihnen wirken. Anhand ihrer Massen berechnest du die Gesamtenergie der Teilchen.
Nun setzt du aus diesen Nukleonen einen Atomkern zusammen. Aufgrund der anziehenden Kräfte, verliert das System an Energie. Die Gesamtenergie reduziert sich also. Die Äquivalenz von Masse und Energie erlaubt es dir, aus dieser Energiedifferenz die Bindungsenergie zu berechnen.
In der Kernphysik bezeichnet die Bindungsenergie die Energie die du brauchst um einen Atomkern in seine Nukleonen zu zerlegen. Vereinen sich die Nukleonen zu so einem Kern, setzen sie eine betragsgleiche Energiemenge frei.
Diese Bindung entsteht durch die starke Kernkraft, welche die abstoßende Coulomb-Kraft der positiv geladenen Protonen überwiegt.
Diese Bindung ist wegen der Äquivalenz von Masse und Energie mit einem Massendefekt verbunden. Das heißt, dass die Masse des Atomkerns geringer ist, als die Summe der Massen seiner Bestandteile. Daher ist es dir Möglich, aus der Masse 
eines Atoms, die Bindungsenergie des Kerns abzuleiten.
Hier steht 
für die Masse des Atoms, 
für dessen Massenzahl, für dessen Ordnungszahl, 
für die Protonenmasse, für die Elektronenmasse, 
für die Neutronenmasse und für die Lichtgeschwindigkeit.
Bindungsenergie berechnen
Als Beispiel, berechnen wir hier die Bindungsenergie des Helium-4-Atoms. Dessen Massendefekt ist 
.
Willst du wissen wie du den Massendefekt berechnest, schau am besten noch in den Artikel zum Massendefekt .
Zunächst rechnest du den Massendefekt in Kilogramm um.
Damit beträgt der Massendefekt in Kilogramm:
Das setzt du nun in die Formel ein.
Die Bindungsenergie des Helium-4-Atoms beträgt also 28,3 MeV (Megaelektronenvolt).
Bindungsenergie pro Nukleon
Zum Abschluss berechnen wird noch die Bindungsenergie pro Nukleon des Helium-4-Atoms. Diese Berechnung ist relativ einfach.
Der Kern des Helium-4-Atoms besteht aus zwei Protonen und zwei Neutronen, insgesamt also aus vier Nukleonen. Die Nukleonenzahl entspricht der Massenzahl .
Damit ergibt sich für die mittlere Bindungsenergie pro Nukleon auf folgende Weise:
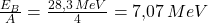
Das heißt also, dass die mittlere Bindungsenergie pro Nukleon des Helium-4-Atoms 7,07 MeV beträgt.
Wie du anhand des Graphen siehst, ist die mittlere Bindungsenergie pro Nukleon für die meisten Kerne im Bereich um 8 MeV. Bei kleinen Massenzahlen jedoch schwankt diese stark.
Im Bereich um 
erreicht die Bindungsenergie ihr Maximum. Bei größeren Massenzahlen fällt sie dann wieder ab.