Massendefekt
Was es mit dem Massendefekt auf sich hat und wo er sich bemerkbar macht erfährst du hier.
Schau am besten noch unser Video an. Hierin haben wir die essentiellen Informationen für dich audiovisuell aufbereitet.
Inhaltsübersicht
Massendefekt einfach erklärt
Betrachtest du einen Atomkern, erkennst du, dass dieser aus Protonen und Neutronen besteht. Nun misst du die Massen dieser Nukleonen individuell und im Anschluss die des Atomkerns. Du stellst fest, dass die Summe der Nukleonenmassen nicht der Masse des Atomkerns entspricht. Der Kern ist leichter als die Summe seiner Bestandteile. Diese Differenz heißt Massendefekt. Damit ist die klassische Aussage der Massenerhaltung widerlegt. Allerdings kannst du über die einsteinsche Äquivalenz von Masse und Energie eine Erklärung finden.
Die Kernbindungsenergie entspricht nämlich genau dem Massendefekt. Je höher dieser ist, desto stabiler ist der Atomkern.
Gleiches gilt auch für das ganze Atom. Misst du dessen Masse und vergleichst diese mit den Massen der individuellen Teilchen, stellst du einen erneuten Massendefekt fest. Dieser ist jedoch deutlich kleiner und kann meistens vernachlässigt werden.
Massendefekt und Bindungsenergie
Der Massendefekt erklärt sich, wenn du die Formel des relativistischen Zusammenhangs zwischen Masse und Energie betrachtest.
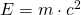
Hierbei steht  für die Energie,
für die Energie,  für die Masse und
für die Masse und  für die Lichtgeschwindigkeit. Die Masse des ruhenden Teilchens gibt Auskunft über dessen Energie. Misst du die Masse des Kerns, ist diese kleiner als die Summe der Massen aller seiner Bestandteile. Die Bindungsenergie vermindert die Masse des Kerns. Mit obiger Formel kannst du die so freigesetzte Bindungsenergie berechnen, indem du für
für die Lichtgeschwindigkeit. Die Masse des ruhenden Teilchens gibt Auskunft über dessen Energie. Misst du die Masse des Kerns, ist diese kleiner als die Summe der Massen aller seiner Bestandteile. Die Bindungsenergie vermindert die Masse des Kerns. Mit obiger Formel kannst du die so freigesetzte Bindungsenergie berechnen, indem du für  den Massendefekt einsetzt. Je größer die Bindungsenergie pro Nukleon, desto stabiler der Kern, da mehr Energie zu dessen Teilung notwendig ist.
den Massendefekt einsetzt. Je größer die Bindungsenergie pro Nukleon, desto stabiler der Kern, da mehr Energie zu dessen Teilung notwendig ist.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Massendefekt Atom und Atomkern
Es ist sehr schwer ein Atom vollständig zu ionisieren und die Masse des Kerns zu bestimmen. Daher wird in der Praxis der Massendefekt  eines neutralen Atoms im nuklearen und elektronischen Grundzustand mit der Masse
eines neutralen Atoms im nuklearen und elektronischen Grundzustand mit der Masse  bestimmt.
bestimmt.

 ist die Masse des Wasserstoff Atoms.
ist die Masse des Wasserstoff Atoms.
Diese Formel hat zwei Summanden, welche du definieren musst.

 ist hierbei das Massenäquivalent der Bindungsenergie des Elektrons im Wasserstoff. Dieser Wert ist bekannt und wird als Rydberg-Energie bezeichnet.
ist hierbei das Massenäquivalent der Bindungsenergie des Elektrons im Wasserstoff. Dieser Wert ist bekannt und wird als Rydberg-Energie bezeichnet.
Die Masse  des neutralen Atoms ist auf ähnliche Weise gegeben.
des neutralen Atoms ist auf ähnliche Weise gegeben.

 ist der Massendefekt der Elektronenhülle. Dies ist das Massenäquivalent der Bindungsenergie aller Elektronen.
ist der Massendefekt der Elektronenhülle. Dies ist das Massenäquivalent der Bindungsenergie aller Elektronen.
Setzt du das in deine ursprüngliche Formel ein heben sie die Massen der Elektronen raus.

Da  viel kleiner ist als
viel kleiner ist als  , wird dieser Term meist vernachlässigt.
, wird dieser Term meist vernachlässigt.
Massendefekt berechnen
Als Beispiel berechnen wir mit dir den Massendefekt und die Bindungsenergie des Helium-4 Kerns.
Der Kern hat eine Masse von  und besteht aus zwei Protonen und zwei Neutronen. Diese haben eine Masse von
und besteht aus zwei Protonen und zwei Neutronen. Diese haben eine Masse von  und
und  .
.
Diese Werte setzt du in deine Formel für den Massendefekt  ein.
ein.

Damit berechnet dieser sich wie folgt:

Die Bindungsenergie  berechnest du über
berechnest du über  .
.

In der Atomphysik wird in der Regel die Energieeinheit des Elektronen-Volts (eV) verwendet.

Damit ergibt sich für deine Bindungsenergie:

Damit hast du berechnet, das ein Helium-4 Kern eine Bindungsenergie von  hat.
hat.

 und Neutronenmasse
und Neutronenmasse  die Masse des Kerns
die Masse des Kerns  abziehst.
abziehst. steht hierbei für die Kernladungszahl und
steht hierbei für die Kernladungszahl und  für die Anzahl der Neutronen.
für die Anzahl der Neutronen.