Knotenpunktverfahren
Du bist dir noch unsicher, was es mit dem Knotenpunktverfahren auf sich hat und wie es funktioniert? Dann können wir dich jetzt beruhigen, denn im nachfolgenden Beitrag erfährst du alles rund um das Verfahren anhand eines Beispiels.
Inhaltsübersicht
Knotenpunktverfahren einfach erklärt
Das Knotenpunktverfahren ist auch unter den Begriffen Rundschnitt oder Knotenschnittverfahren bekannt. Es wird hauptsächlich auf Fachwerke angewandt. Die Idee ist dabei einzelne Knoten freizuschneiden, um die Kräfte, die an diesem angreifen, zu bestimmen. Dabei muss sich jeder Knoten in einem kraftmäßigem Gleichgewicht befinden. Am besten fängt man dabei beim Knoten mit den wenigsten unbekannten Stabkräften an. In dem Video, welches wir dir hier verlinkt haben, erklären wir dir die Grundlagen zu der Bauweise von idealisierten Fachwerken. Zusätzlich erfährst du in diesem Videobeitrag alles rund um das Kräfte– beziehungsweise Momentengleichgewicht.
Knotenpunktverfahren Beispiel
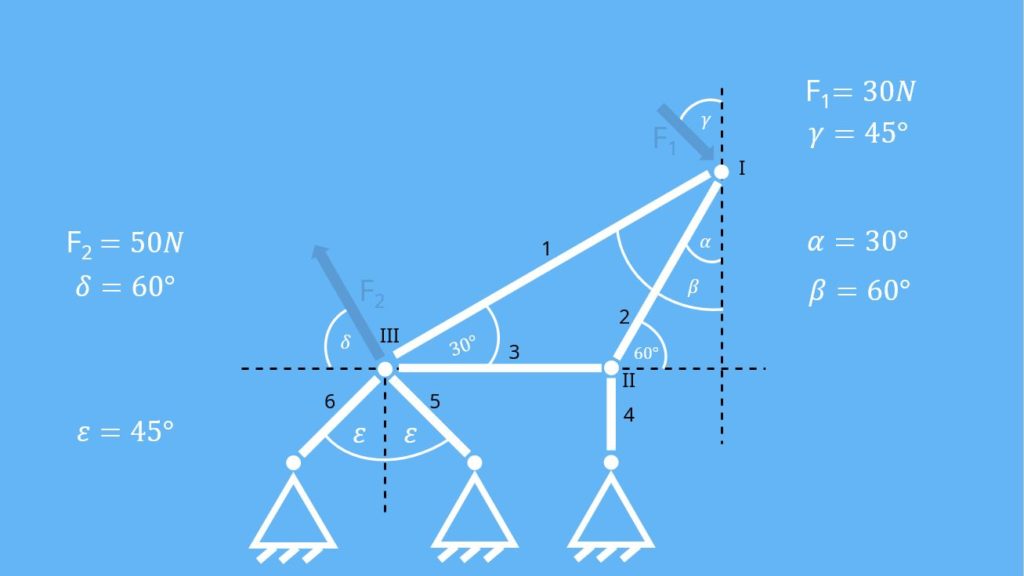
Dann können wir jetzt mit dem Knotenpunktverfahren loslegen. Als Beispiel nehmen wir ein Fachwerk, welches auf drei Festlagern gebaut ist. Zu den einzelnen Lagern erfährst du in diesem
Video mehr. Wir kennen die Winkel 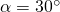 ,
, 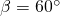 und
und 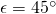 . An unserem Fachwerk greifen jetzt die Kräfte
. An unserem Fachwerk greifen jetzt die Kräfte 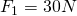 unter dem Winkel
unter dem Winkel 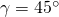 und
und 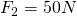 unter dem Winkel
unter dem Winkel 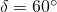 an.
an.
Um eine bessere Übersicht im Knotenpunktverfahren zu behalten, nummerieren wir alle Stäbe und Knoten: Die Stäbe von oben nach unten von eins bis sechs, den oberen Knoten als I, den unteren rechten als II und den linken als III. Hier lohnt es sich wieder die Werte erst in die Ergebnisgleichung des Knotenschnittverfahrens einzusetzen, wenn alle bekannt sind.
Winkelbestimmung
Jetzt müssen wir noch die restlichen Winkel für das Knotenpunktverfahren bestimmen. Der Winkel zwischen Stab eins und drei entsteht, indem man ein imaginäres Dreieck mit einem rechten Winkel und 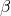 spannt. Außerdem ergibt sich, dass der Winkel zwischen Stab eins und drei
spannt. Außerdem ergibt sich, dass der Winkel zwischen Stab eins und drei 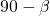 ist. Weiterhin brauchen wir noch den Winkel zwischen Stab zwei und der Horizontalen. Den bestimmen wir ähnlich: Wir stellen uns wieder ein Dreieck mit
ist. Weiterhin brauchen wir noch den Winkel zwischen Stab zwei und der Horizontalen. Den bestimmen wir ähnlich: Wir stellen uns wieder ein Dreieck mit 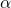 und einem rechten Winkel vor und finden heraus, dass der Stab zwei um
und einem rechten Winkel vor und finden heraus, dass der Stab zwei um 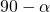 geneigt ist.
geneigt ist.
Knoten freischneiden und Kräftegleichgewicht
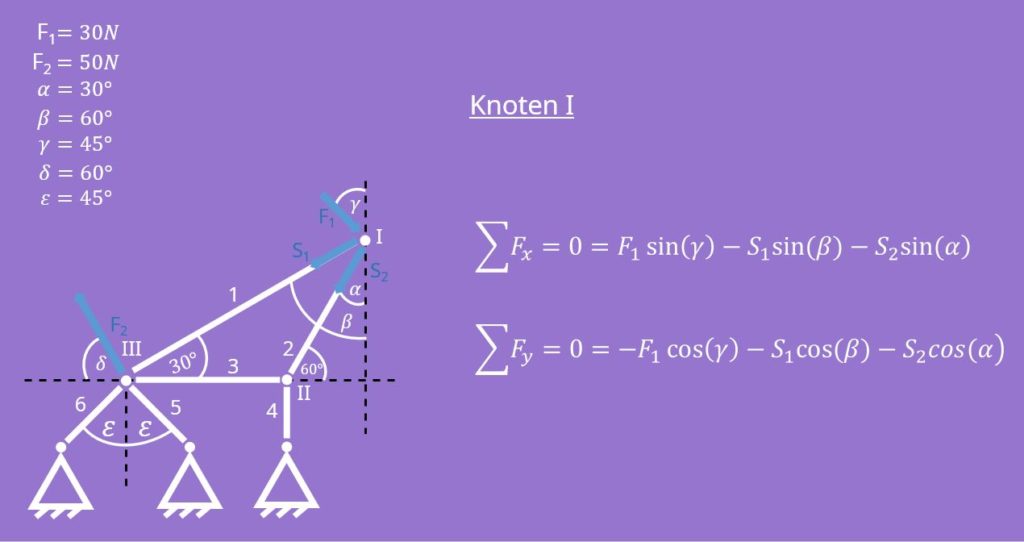
Im nächsten Schritt des Knotenschnittferfahrens schneiden wir jeden einzelnen Knoten frei und bilden ein Kräftegleichgewicht in x- und y-Richtung. Wir beginnen bei Knoten I:
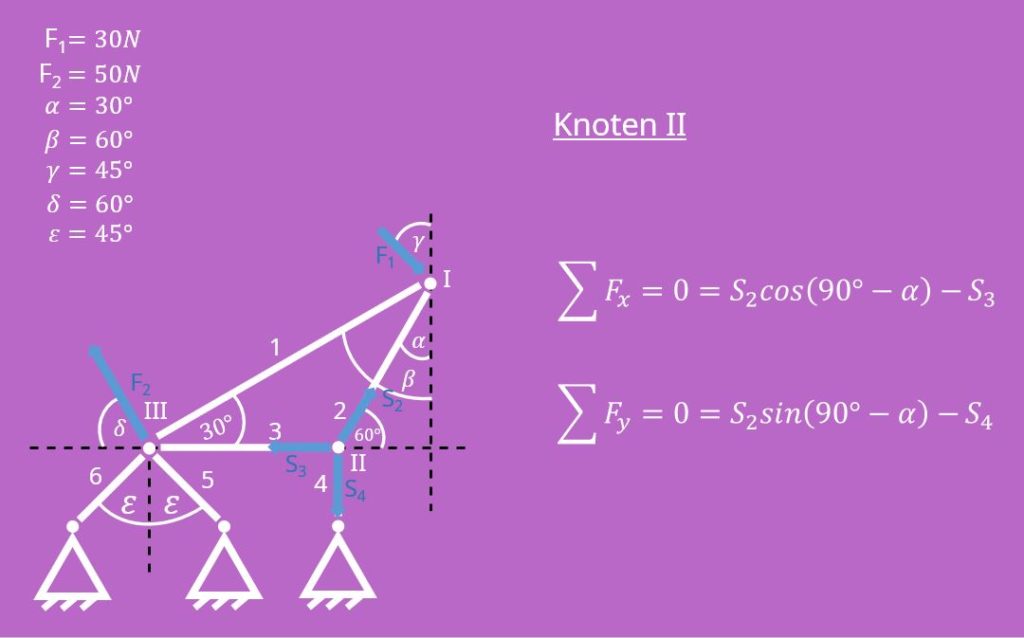
Als nächstes bei Knotenschnittverfahren schneiden wir den Knoten II frei und stellen wiederrum das Kräftegleichgewicht in x- und y-Richtung auf:
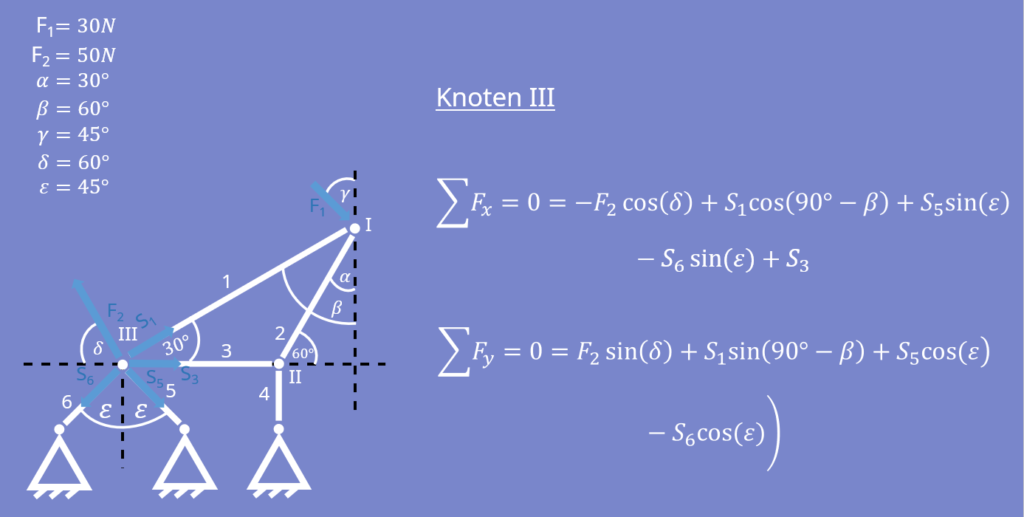
Zum Schluss schneiden wir den dritten Knoten frei und bilden das Kräftegleichgewicht:
Knoten berechnen
Nachdem wir nun die Gleichungen aufgestellt haben, fangen wir an, diese nach unseren Unbekannten umzustellen. Als erstes nehmen wir den Knoten mit den wenigsten unbekannten Größen. In unserem Fall ist das der Knoten I: Hier stellen wir unsere Gleichung in x-Richtung nach 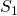 um und erhalten:
um und erhalten:
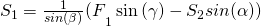
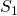 setzen wir nun in die Gleichung für die y-Richtung ein. Damit wird der erhaltene Term für
setzen wir nun in die Gleichung für die y-Richtung ein. Damit wird der erhaltene Term für 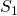 in der Gleichung für die y-Richtung mit
in der Gleichung für die y-Richtung mit 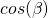 multipliziert:
multipliziert:
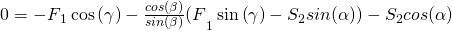
Als nächstes sortieren wir die Gleichung nach 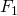 und
und 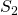 und erhalten:
und erhalten:
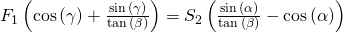
Jetzt müssen wir nur noch durch die Klammer hinter 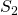 teilen. Um uns Schreibarbeit zu ersparen, multiplizieren wir den Term mit der Klammer hoch
teilen. Um uns Schreibarbeit zu ersparen, multiplizieren wir den Term mit der Klammer hoch 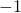 .
.
Wenn wir das wieder in unsere Gleichung für 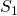 einsetzen, erhalten wir für
einsetzen, erhalten wir für 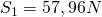 und haben so mit dem Knotenpunktverfahren den ersten Knoten berechnet.
und haben so mit dem Knotenpunktverfahren den ersten Knoten berechnet.
Ab jetzt kennen wir schon einige Unbekannte und das Knotenpunktverfahren wird deutlich einfacher.
Betrachten wir jetzt den zweiten Knoten, sehen wir, dass wir nach 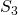 und
und 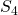 umstellen können und erhalten
umstellen können und erhalten 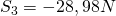 und für
und für 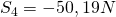 .
.
Als letzten Schritt des Knotenschnittverfahrens können wir uns dem dritten Knoten widmen. Bei diesem sehen die Gleichungen zwar am komplexesten aus, sind aber durch die Ergebnisse, die wir durch das Knotenpunktverfahren vorher bestimmt haben, einfach zu lösen. Als erstes stellen wir die Gleichung in x-Richtung nach 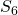 um und erhalten:
um und erhalten:
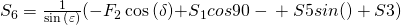
Das setzen wir danach in die Gleichung für die y-Richtung ein und erhalten 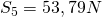 .
.
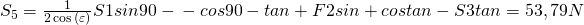
Das können wir wieder in die Gleichung für 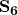 einsetzen. Die letzte Unbekannte Stabkraft
einsetzen. Die letzte Unbekannte Stabkraft 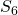 ist dann gleich
ist dann gleich 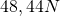 . Damit sind alle Unbekannten berechnet und das Knotenschnittverfahren ist beendet.
. Damit sind alle Unbekannten berechnet und das Knotenschnittverfahren ist beendet.