Losgrößenmodell bei Eigenproduktion
Bei der Eigenproduktion stellst du die Armbänder selbst her. In der Supply Chain befinden wir uns hier in der Phase der Produktion. Wie du die optimale Losgröße bei Eigenproduktion mit der Andler Formel berechnen kannst, zeigen wir dir hier!
Wenn du eher der audiovisuelle Lerntyp bist, dann schau dir direkt unser Video zum Losgrößenmodell bei Eigenproduktion an.
Inhaltsübersicht
Bestimmung des Losgrößen in der Eigenproduktion
Um die optimale Losgröße und die optimalen Produktionsabstände herauszufinden, schauen wir uns wie beim Video zum Losgrößenmodell bei Fremdbeschaffung eine Grafik dazu an:
Im Vergleich zum Fall der Fremdbeschaffung erweitert sich hier unser Modell um die Variable x. Diese ist die Produktionsgeschwindigkeit, mit der das Los in das Lager kommt. Dabei kommt es nicht wie bei der Bestellung zeitpunktgeballt in das Lager, sondern nach und nach.
Kostenfunktion für die Optimale Losgröße
Schauen wir uns nun an, wie sich die Kostenfunktion zusammensetzt. Sie besteht zum einen, wie bei der Fremdbeschaffung, aus den Lagerkosten, also den Kapitalbindungskosten, und zum anderen aus den losfixen Kosten. Die Kapitalbindungskosten sind hier nun geringer, da der Bestand ja nicht auf einmal, sondern mit der Produktionsgeschwindigkeit zunimmt. Das wird in der Formel berücksichtigt.
Sie erweitert sich um die Komponente  .
.
Unter losfixen Kosten versteht man die Rüstkosten. Das sind die Kosten, die dadurch entstehen, dass wir die Maschine auf die Produktion von Uhrenbändern vorbereiten müssen. Das können Personalkosten, Opportunitätskosten für entgangene Deckungsbeiträge oder Materialverlust sein. Um die losfixen Kosten herauszufinden, teilen wir auch hier unsere Fixkosten F einfach durch die Bestellzykluslänge t.

Grafisch sieht das genauso aus wie bei Fremdbeschaffung der Uhrenbänder.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Optimale Losgröße bei Eigenproduktion – Andler Formel
Leiten wir unsere neue Kostenfunktion nach der Produktionsmenge q ab, erhalten wir die Andler Formel:

Im Folgenden nehmen wir an, dass dir pro Rüstvorgang Kosten in Höhe von 500€ entstehen. Die Bedarfsrate beträgt 500 Bänder pro Woche und die Produktionsgeschwindigkeit 30 Stück pro Stunde. Beachte aber, dass du die Produktionsgeschwindigkeit noch in Wochen umrechnen musst. Hat eine Woche 80 Arbeitsstunden beträgt unsere Produktionsgeschwindigkeit also 2400 Stück pro Woche:
Optimale Losgröße berechnen bei Eigenpoduktion – Andler Formel
Jetzt können wir alle Werte ganz einfach in die Andler Formel einsetzen und erhalten unsere optimale Losgröße:

Du solltest also 3697 Uhrenbänder in einem Los produzieren.
Optimale Zeitabstände für die Optimale Losgröße
Aber in welchen Zeitabständen soll produziert werden? Um das herauszufinden, teilen wir einfach wie vorhin unser optimales Produktionslos durch die Bedarfsrate:
Die Kosten sind also minimal, wenn du alle 7,4 Wochen 3697 Uhrenbänder produzierst.
Kosten berechnen für die Optimale Losgröße
Wenn wir jetzt noch die wöchentlichen Kosten berechnen wollen, wenn wir die optimale Losgröße produzieren, setzen wir diese wie vorhin einfach in unsere Kostenfunktion ein:
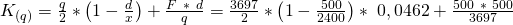

Es entstehen dir also Kosten von 135,23 € pro Woche bei Eigenherstellung der Uhrenbänder.
Jetzt weißt du, wie du die optimale Losgröße und die optimale Bestellmenge mit der Andler Formel ermitteln kannst.



