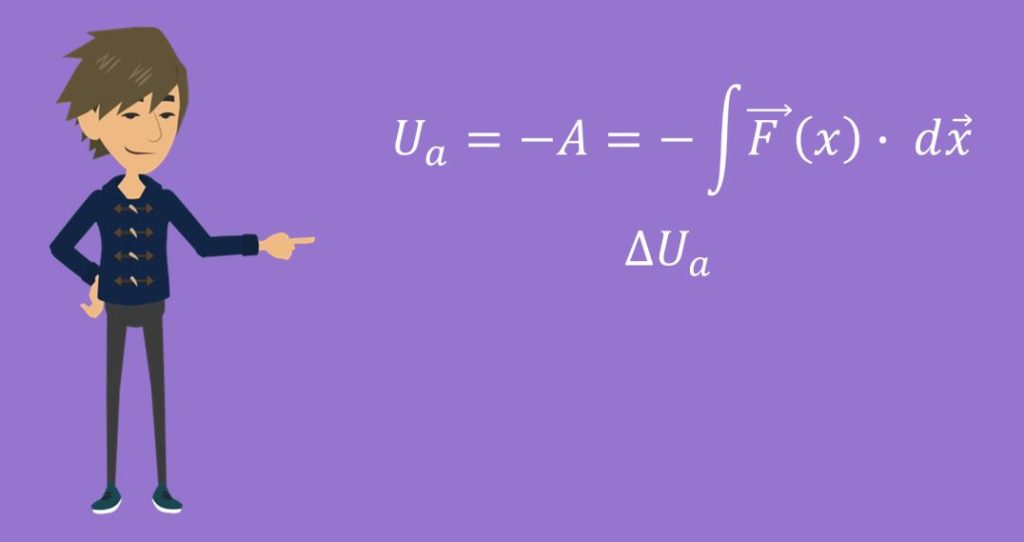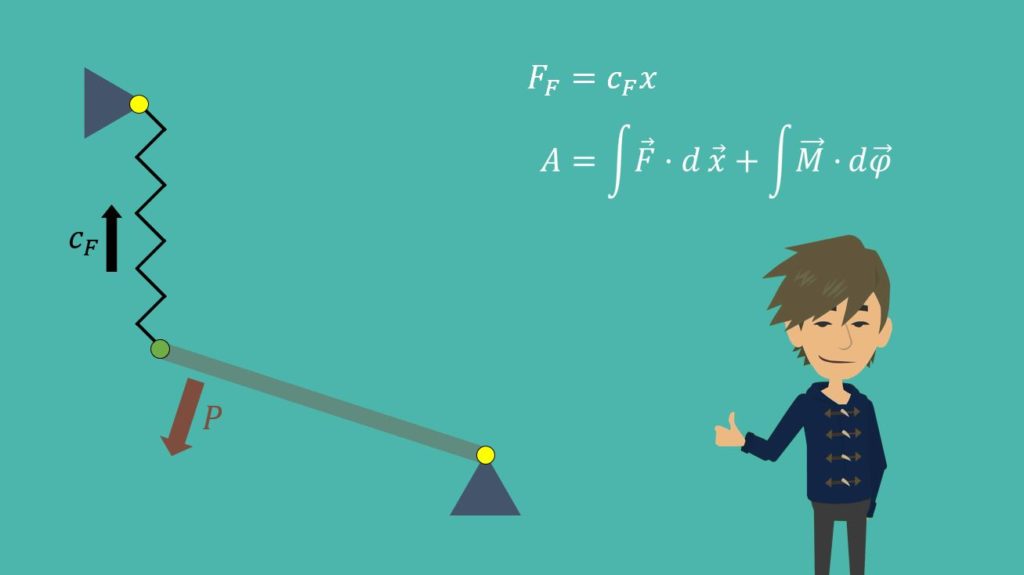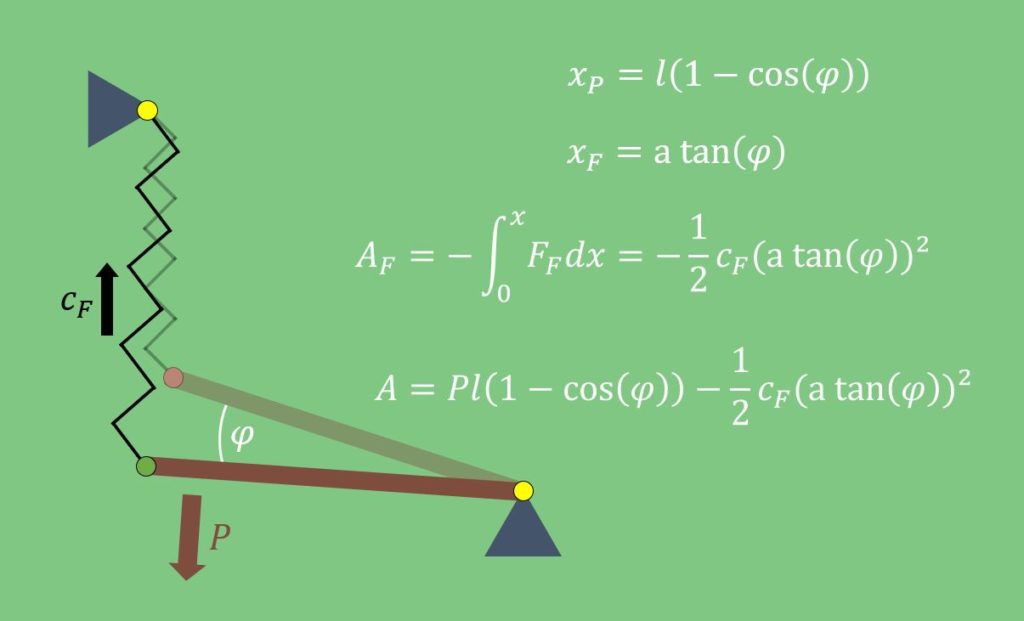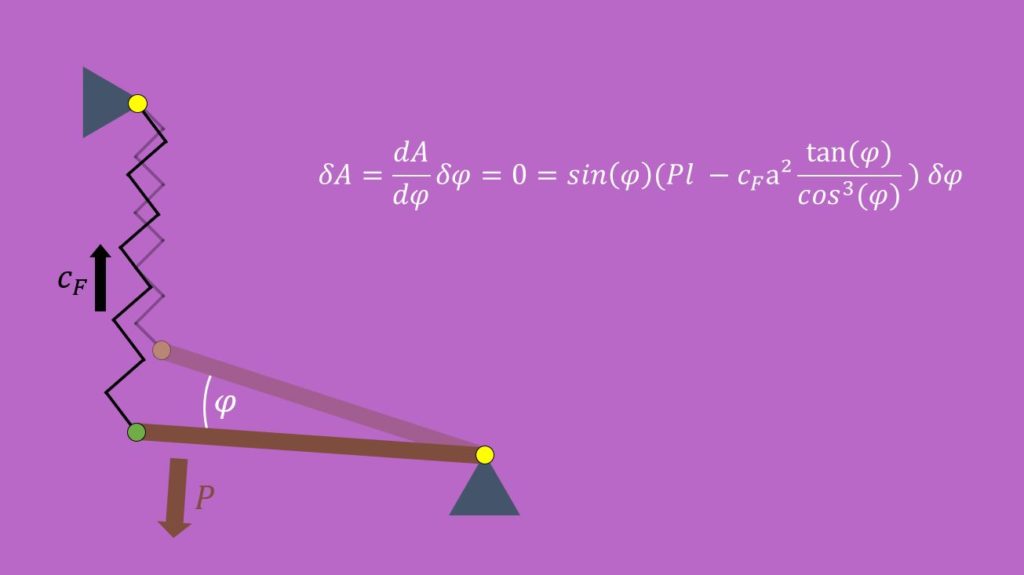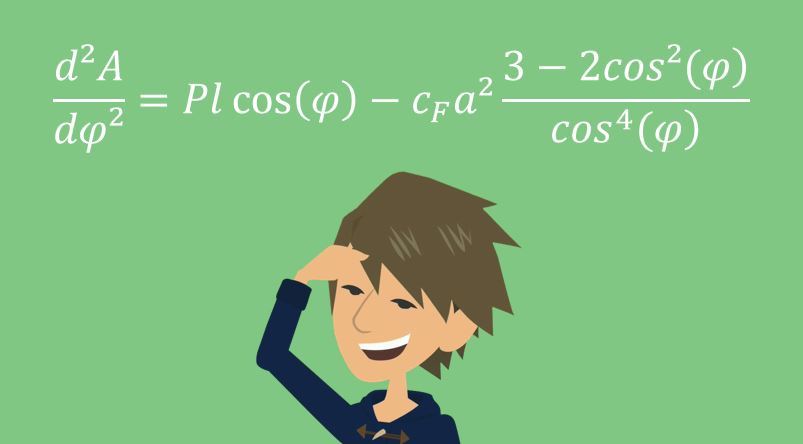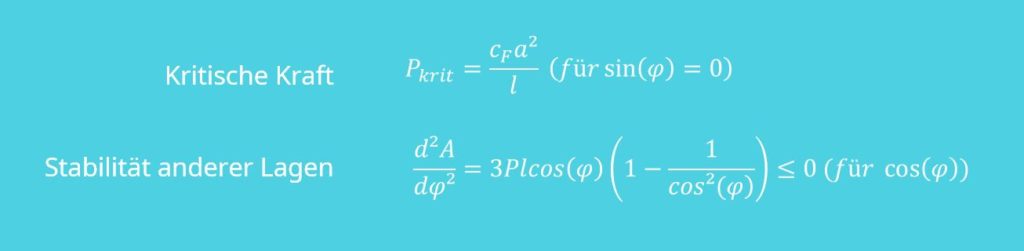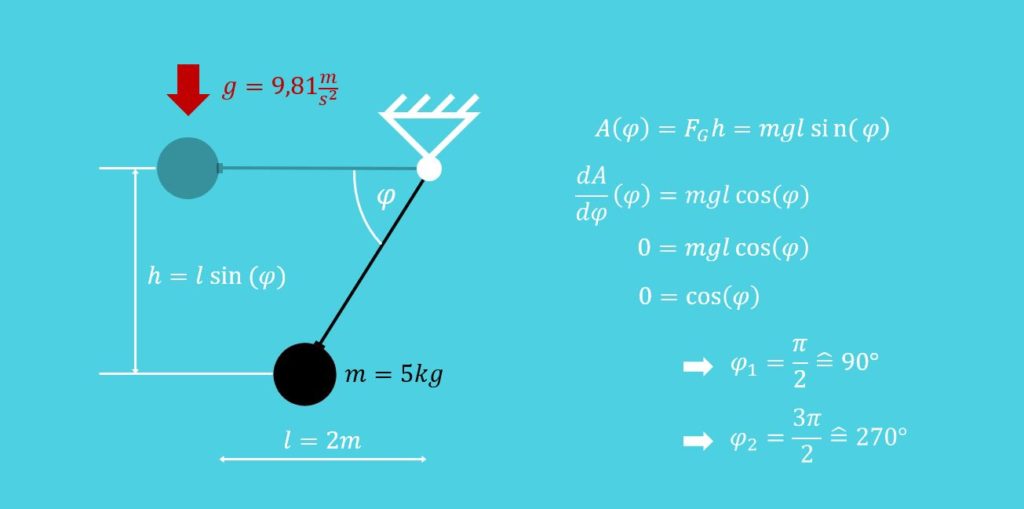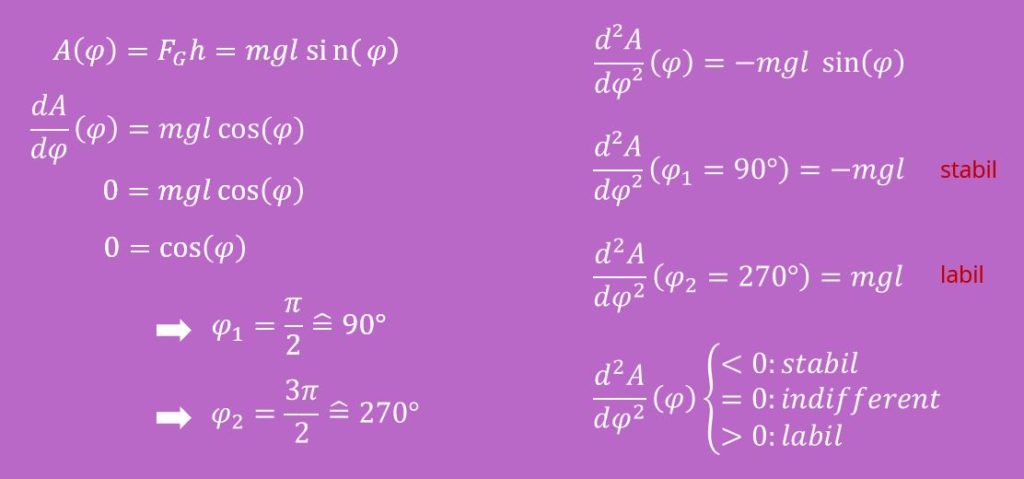Gleichgewichtslage
Was man unter der Gleichgewichtslage versteht, erfährst du hier. Außerdem erklären wir dir die Unterschiede zwischen dem stabilen, dem indifferenten und dem labilen Gleichgewicht. In unserem Video erfährst du das Alles in kürzester Zeit. Schau doch mal rein.
Inhaltsübersicht
Gleichgewichtslage einfach erklärt
Du fragst dich, warum du überhaupt lernen musst, wann ein System stabil ist und wie es sich mit der Gleichgewichtslage verhält? Im Endeffekt willst du damit nur herausfinden, ob das System, das du gerade betrachtest, belastbar genug ist für das, was du damit vorhast. Außerdem will man oftmals wissen, ob es sich um ein stabiles, ein indifferentes oder ein labiles Gleichgewicht handelt. Außerdem kannst du so herausfinden, welche Kraft oder welches Moment du maximal aufbringen kannst, bevor das System instabil wird, also quasi „kaputt“ geht.
Insgesamt unterscheiden wir in drei verschiedene Arten der Gleichgewichtslagen:
Stabiles Gleichgewicht
Nach einer Störung würde das System, welches sich in diesem Gleichgewicht befindet, wieder in seine Ursprungslage zurückkehren.
Neutrales Gleichgewicht
Bei einer Störung des neutralen oder auch indifferenten Gleichgewichtssystem, entsteht ein neuer Gleichgewichtszustand, in dem das System zur Ruhe kommt.
Labiles Gleichgewicht
Hier geht das System bei der kleinsten Störung in einen neuen Zustand über.
Gleichgewichtslage – Beispiel Ball
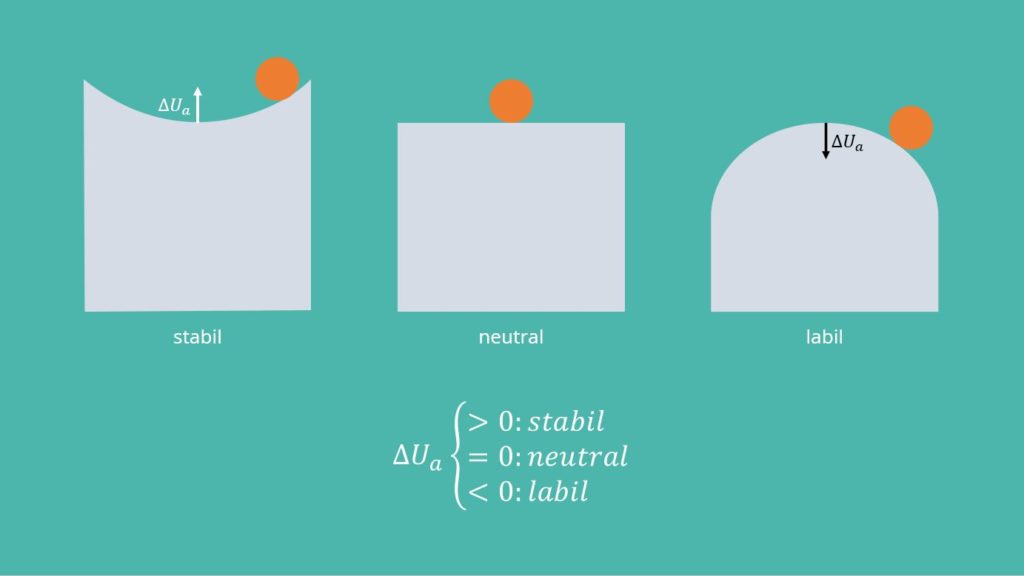
Für eine anschaulichere Vorstellung der verschiedenen Gleichgewichtslagen, denken wir uns einen Ball auf unterschiedlichen Untergründen.
- Der Ball liegt in einer Kuhle
- Der Ball liegt auf einer geraden Fläche
- Der Ball liegt auf der Spitze eines Hügels
Nun verändern wir die Gleichgewichtslage des Balles leicht. Du kannst dir sicher vorstellen, was dann passiert: Der Ball in der Kuhle rollt zurück, der Ball auf der Spitze des Hügels rollt den Berg hinunter und der Ball auf der geraden Fläche bleibt da liegen, wo er hinbewegt wurde. Daraus ergibt sich, dass im ersten Fall ein stabiles Gleichgewicht vorherrscht, im zweiten Fall ein indifferentes Gleichgewicht und im dritten Fall ein labiles Gleichgewicht. Stabil ist ein System also dann, wenn die Gleichgewichtslage wiederhergestellt werden kann.
Gleichgewichtslage und Potential
Doch wie sieht die Gleichgewichtslage bei komplexeren Systemen aus? Dazu betrachten wir einfach wieder die Potentiale. Zur Erinnerung: Das Potential 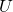 ist definiert als die negative Arbeit einer konservativen Kraft. Wir betrachten im Genaueren eine Potentialdifferenz
ist definiert als die negative Arbeit einer konservativen Kraft. Wir betrachten im Genaueren eine Potentialdifferenz 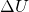 , was einfach nur bedeutet, dass wir uns das Potential an zwei verschiedenen Punkten anschauen.
, was einfach nur bedeutet, dass wir uns das Potential an zwei verschiedenen Punkten anschauen.
Betrachten wir nun wieder den Ball: Im ersten Fall steigt das Potential und die Differenz ist positiv, im zweiten Fall ändert sich nichts, also existiert ein indifferentes Gleichgewicht und im dritten Fall fällt das Potential und wir haben eine Differenz kleiner null. Daraus kann man allgemein herleiten, dass Folgendes gelten muss:
Gleichgewichtslage, Potential und Definition Arbeit
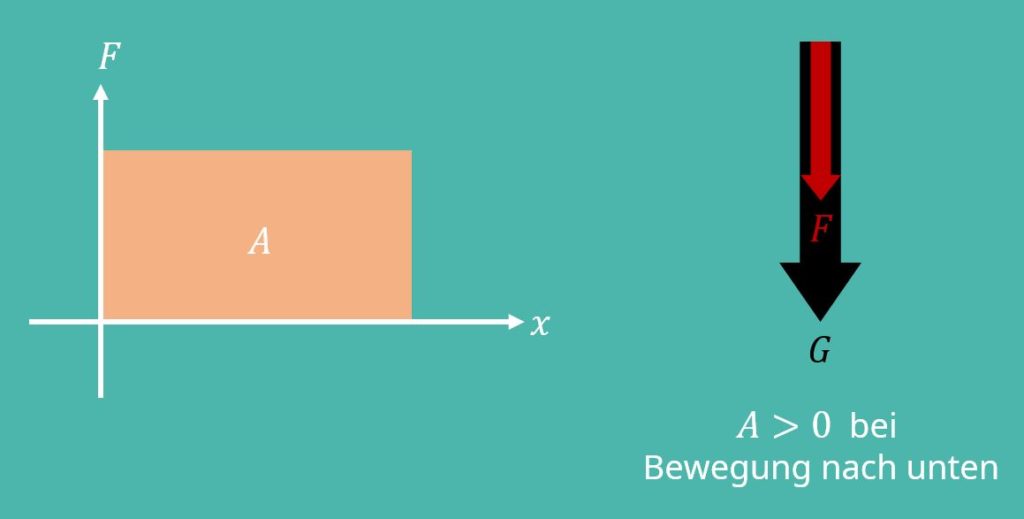
Nun ist es schwierig etwas über das Potential direkt zu sagen. Deshalb verwenden wir einfach die Definition über die Arbeit. Diese ist der Weg, der infolge einer Kraft zurückgelegt wird. Dabei ist die Arbeit in Kraftrichtung positiv definiert. Zur Erinnerung: Die Gewichtskraft ist positiv nach unten, und somit ist die Arbeit positiv bei einer Bewegung nach unten. Da wir nun keinen definierten Weg gehen, haben wir eine Funktion, bei der eine Abhängigkeit vom Weg besteht. Das werden wir später noch brauchen.
Mit Hilfe eines mathematischen Tricks, der sogenannten Taylorentwicklung, auf die wir hier genauer eingehen, ergibt sich, dass 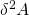 relevant für die Stabilität ist. Doch was hat das jetzt schon wieder mit der Gleichgewichtslage zu tun und wie finden wir heraus, ob es sich um ein stabiles Gleichgewicht, ein indifferentes Gleichgewicht oder ein labiles Gleichgewicht handelt? Im Endeffekt beschreibt
relevant für die Stabilität ist. Doch was hat das jetzt schon wieder mit der Gleichgewichtslage zu tun und wie finden wir heraus, ob es sich um ein stabiles Gleichgewicht, ein indifferentes Gleichgewicht oder ein labiles Gleichgewicht handelt? Im Endeffekt beschreibt 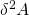 nur die zweite Ableitung der Arbeit. Die zweite Ableitung könnte dir wieder aus der Schule bekannt vorkommen und zwar aus der Berechnung der Hoch- und Tiefpunkte. Mit Hilfe der Überlegung vorher ergibt sich für die Betrachtung folgender Zusammenhang:
nur die zweite Ableitung der Arbeit. Die zweite Ableitung könnte dir wieder aus der Schule bekannt vorkommen und zwar aus der Berechnung der Hoch- und Tiefpunkte. Mit Hilfe der Überlegung vorher ergibt sich für die Betrachtung folgender Zusammenhang:
Beispiel Federstab
Das schaut jetzt natürlich sehr abstrakt aus, doch eigentlich ist es gar nicht so schwer, die Gleichgewichtslage zu bestimmen. Betrachten wir nun einen Stab, der am Boden nur mit einem Momentengelenk befestigt ist und von links mit einer Feder gehalten wird. Wir wollen jetzt herausfinden, mit welcher Kraft 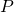 wir den Stab belasten können.
wir den Stab belasten können.
Bei der Betrachtung der Stabilität bietet sich das Prinzip der virtuellen Verrückung an, da bei beiden Verfahren die Arbeit zentral ist. Als erstes überlegen wir uns wieder, wodurch Arbeit verursacht werden kann: Durch die Kraft 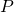 und die Federkraft. Die Federkraft ist definiert als:
und die Federkraft. Die Federkraft ist definiert als:
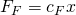
Hier bildet 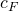 die Federkonstante. Wie du weißt, wirkt sie immer entgegen der Bewegungsrichtung und ist somit keine konservative Kraft.
die Federkonstante. Wie du weißt, wirkt sie immer entgegen der Bewegungsrichtung und ist somit keine konservative Kraft.
Wir kennen zudem die allgemeine Definition der Arbeit:
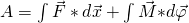
Unsere äußere Last ist konservativ, weshalb wir hierfür das Integral sehr einfach lösen können. Wir suchen nur den Weg, den die Kraft nach unten zurücklegt, wenn sich der Stab um den Winkel 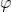 dreht:
dreht:
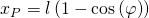
Da die Federkraft nicht konservativ ist, müssen wir hier das Integral lösen. Dazu betrachten wir wieder den Weg bei einer Auslenkung um 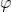 :
:
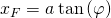
Wir haben jetzt eine Abhängigkeit von 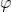 und können das Integral nach
und können das Integral nach 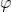 integrieren und erhalten:
integrieren und erhalten:
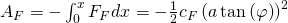
Das negative Vorzeichen kommt daher, dass der Weg, den wir gehen, immer entgegengesetzt der Kraftrichtung ist.
Daraus ergibt sich dann für die Arbeit, die verrichtet wird, infolge einer Drehung um 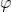 :
:
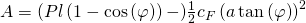
Mit Hilfe des Prinzips der virtuellen Verrückung und eines mathematschen Tricks erhalten wir folgende Formel:
Der mathematische Trick besteht darin, dass wir die Arbeit nach 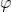 ableiten und wieder mit
ableiten und wieder mit 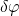 multiplizieren, um
multiplizieren, um 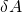 zu bekommen. Und aus dem Prinzip der virtuellen Verrückung wissen wir, dass für statisch bestimmte System
zu bekommen. Und aus dem Prinzip der virtuellen Verrückung wissen wir, dass für statisch bestimmte System 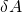 gleich null sein muss.
gleich null sein muss.
Damit kennen wir nun auch die Gleichgewichtslagen unseres Systems:
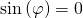
![Rendered by QuickLaTeX.com \cos{\left(\varphi\right)}=\sqrt[3]{\frac{c_Fa^2}{Pl}}](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-72c4d9ae7cb38054488b0d2bdeca51f2_l3.png)
Jetzt wollen wir wissen, welche Art von Gleichgewichtslage diese Lagen sind. Dafür machen wir das Gleiche wie bei der Arbeit und differenzieren wieder nach 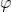 . Dieses Mal brauchen wir allerdings nicht mit
. Dieses Mal brauchen wir allerdings nicht mit 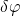 multiplizieren. Wir haben hier also die zweite Ableitung der vorher bestimmten Funktion:
multiplizieren. Wir haben hier also die zweite Ableitung der vorher bestimmten Funktion:
Jetzt müssen wir nur noch die, aus dem Prinzip der virtuellen Verrückung gewonnene jeweilige Gleichgewichtslage einsetzen. Dazu werden die beiden Lagen nach 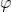 umgeformt, da dies unsere einzige Variable ist.
umgeformt, da dies unsere einzige Variable ist.
Aus Sinus von 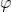 gleich null erhalten wir unsere kritische Kraft, bei der unser System anfängt sich zu bewegen. Aus der zweiten Gleichgewichtslage können wir eine Aussage über die Stabilität in anderen Lagen treffen. Es ergibt sich durch das Einsetzen folgender Zusammenhang:
gleich null erhalten wir unsere kritische Kraft, bei der unser System anfängt sich zu bewegen. Aus der zweiten Gleichgewichtslage können wir eine Aussage über die Stabilität in anderen Lagen treffen. Es ergibt sich durch das Einsetzen folgender Zusammenhang:
Das heißt, wir kennen jetzt die Kraft, die bei 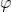 gleich null aufgegeben werden darf, damit keine Auslenkungen zu sehen sind und wissen, dass für alle anderen Auslenkungen unser System stabil ist. Das können wir wieder aus unserer vorherigen Überlegung schließen, bei der wir festgestellt haben, dass die zweite Ableitung der Arbeit kleiner null sein muss, damit unser System stabil ist und wir ein stabiles Gleichgewicht haben. Du siehst, dass der Term für
gleich null aufgegeben werden darf, damit keine Auslenkungen zu sehen sind und wissen, dass für alle anderen Auslenkungen unser System stabil ist. Das können wir wieder aus unserer vorherigen Überlegung schließen, bei der wir festgestellt haben, dass die zweite Ableitung der Arbeit kleiner null sein muss, damit unser System stabil ist und wir ein stabiles Gleichgewicht haben. Du siehst, dass der Term für 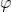 gleich null auch null ist. Für den Fall aber, haben wir ja eine kritische Kraft gefunden, bis zu der keine Bewegung stattfinden wird.
gleich null auch null ist. Für den Fall aber, haben wir ja eine kritische Kraft gefunden, bis zu der keine Bewegung stattfinden wird.
Nun haben wir die verschiedenen möglichen Gleichgewichtslagen und das dazugehörige Potential kennengelernt. Im Folgenden soll dies noch einmal vertieft behandelt werden. Dabei kannst du dir auch das hier verlinkte Video dazu anschauen.
Gleichgewichtslage berechnen
Als erstes fassen wir noch einmal die Grundlagen zusammen:
Um herauszufinden, ob und wo ein System ein stabiles Gleichgewicht, ein indifferentes Gleichgewicht oder ein labiles Gleichgewicht hat, betrachten wir in der Regel das Potential beziehungsweise die Arbeit, aus der sich das Potential ergibt. Dazu überlegen wir uns vorher, welche Bewegung das System vollführen kann und stellen eine Gleichung für die Arbeit in Abhängigkeit einer Laufvariablen auf, die die Bewegung beschreibt.
Als nächstes ermitteln wir die Gleichgewichtslage des Systems, indem wir die Gleichung für die Arbeit ableiten, gleich null setzen und dann lösen. Vergleichbar ist das mit der Ermittlung der Extrempunkte einer Funktion. Als letztes überprüfen wir, ob die jeweilige Gleichgewichtslage stabil ist. Dazu leiten wir die Gleichung der Arbeit ein weiteres Mal ab und setzen unsere gefundenen Ergebnisse in die zweite Ableitung ein. Um nun eine Aussage über die Stabilität machen zu können, betrachten wir das Vorzeichen. Es gilt:
Wenn die zweite Ableitung kleiner null ist, handelt es sich um ein stabiles Gleichgewicht. Ist sie gleich null, können wir von einem indifferenten Gleichgewicht ausgehen und ist sie größer null, dann ist das Gleichgewicht labil. Wichtig ist, dass 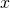 nur stellvertretend für die Laufvariable steht und nicht generell verwendet werden kann. Das klingt zwar komplex, aber du wirst gleich sehen, dass es gar nicht so schwer ist.
nur stellvertretend für die Laufvariable steht und nicht generell verwendet werden kann. Das klingt zwar komplex, aber du wirst gleich sehen, dass es gar nicht so schwer ist.
Beispiel Pendel
Nachdem wir die Theorie in Bezug auf das stabile Gleichgewicht, das indifferente Gleichgewicht und das labile Gleichgewicht wieder parat haben, betrachten wir nun ein weiteres Beispiel zur Gleichgewichtslage: Ein einfaches Pendel mit der Länge 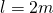 , an dem am Ende eine Masse mit
, an dem am Ende eine Masse mit 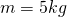 hängt. Wir gehen davon aus, dass das Pendel eine starre Stange ist und sich das System logischerweise im Erdschwerefeld befindet. Das heißt, wir haben eine Erdbeschleunigung von
hängt. Wir gehen davon aus, dass das Pendel eine starre Stange ist und sich das System logischerweise im Erdschwerefeld befindet. Das heißt, wir haben eine Erdbeschleunigung von 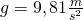 . Zu Beginn ist das Pendel in der Waagerechten festgehalten.
. Zu Beginn ist das Pendel in der Waagerechten festgehalten.
Wenn wir das Pendel nun loslassen, dreht es sich um die Befestigung. Dementsprechend nehmen wir als Laufvariable den Winkel 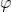 , um den sich das Pendel gegenüber der Ausgangslage bewegt.
, um den sich das Pendel gegenüber der Ausgangslage bewegt.
Als erstes stellen wir die Gleichung für die Arbeit auf: Da in unserem Fall nur die Gewichtskraft der Masse angreift, ist diese relativ schnell aufgestellt. Die Gewichtskraft zeigt immer nach unten. Deshalb müssen wir nur den Weg 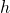 nach unten betrachten. Dieser ist natürlich wiederrum abhängig von
nach unten betrachten. Dieser ist natürlich wiederrum abhängig von 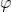 und ergibt sich zu:
und ergibt sich zu:
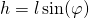
Daraus resultiert dann für die Arbeit:
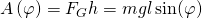
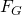 ist dabei die Gewichtskraft gleich
ist dabei die Gewichtskraft gleich 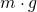 .
.
Nachdem wir eine Gleichung für die Arbeit haben, bilden wir die erste Ableitung nach unserer Laufvariablen 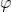 und erhalten:
und erhalten:
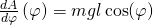
Die erste Ableitung setzen wir jetzt gleich null und suchen Lösungen für 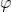 :
:
Das heißt, unsere jeweilige Gleichgewichtslage ist bei 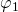 gleich
gleich 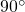 senkrecht UNTER der Aufhängung und bei
senkrecht UNTER der Aufhängung und bei 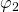 gleich
gleich 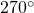 senkrecht ÜBER der Aufhängung.
senkrecht ÜBER der Aufhängung.
Zum Schluss treffen wir noch eine Aussage über die Stabilität. Dazu bilden wir die zweite Ableitung:
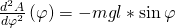
Jetzt müssen wir nur noch jeweils die gefundene Gleichgewichtslage einsetzen. Wie du bereits weißt, gilt:
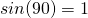 und
und 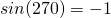
Damit ergibt sich für die Gleichgewichtslage:
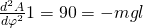
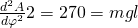
Erinnern wir uns jetzt zurück an die Bedingungen über die Stabilität, erkennen wir, dass 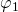 gleich 90° ein stabiles Gleichgewicht ist, da das Vorzeichen in jedem Fall negativ ist und
gleich 90° ein stabiles Gleichgewicht ist, da das Vorzeichen in jedem Fall negativ ist und 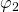 gleich 270° ein instabiles Gleichgewicht ist, da das Vorzeichen auch hier nicht wechseln kann. Du erkennst, dass wir keine Abhängigkeit vom System, sondern feste Winkel und damit Positionen haben. Das deckt sich auch mit unserer physikalischen Intuition.
gleich 270° ein instabiles Gleichgewicht ist, da das Vorzeichen auch hier nicht wechseln kann. Du erkennst, dass wir keine Abhängigkeit vom System, sondern feste Winkel und damit Positionen haben. Das deckt sich auch mit unserer physikalischen Intuition.