Dualer Simplex
Du hast dich schon mit dem Simplex Algorithmus beschäftigt? Super, dann wird dir der duale Simplex keine großen Probleme bereiten. Aber selbst wenn dir der Simplex Algorithmus noch Schwierigkeiten bereitet, kein Problem! Im folgenden Beitrag erklären wir dir den dualen Simplex – auf englisch dual Simplex – Schritt für Schritt mit Hilfe einer Beispielrechnung.
Inhaltsübersicht
Dualer Simplex: Beispiele und Erklärungen
Den dualen Simplex Algorithmus verwendet man – anders als den primalen Simplex – wenn negative rechte Seiten vorhanden sind. Ansonsten gilt weiterhin, dass sich in der Normalform eine Einheitsmatrix unter den Schlupfvariablen bilden muss. Außerdem muss die Zielfunktion maximierend sein.
Dualer Simplex Beispiel:
Der Ablauf des dualen Simplex ist ähnlich wie beim primalem Simplex. Wir gehen ihn anhand dieses Beispiels durch: Im folgenden Teil zeigen wir dir das Vorgehen Schritt für Schritt anhand eines Beispiels. Dafür stellen wir die Normalform auf:
Um mit dem ersten Schritt beginnen zu können, müssen wir noch die Normalform in das Simplextableau übertragen:
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Dualer Simplex – Erster Schritt:
Als erstes wählen wir nun wieder die Pivotzeile z. Gibt es keine negativen rechten Seiten, also ist bi größer gleich 0, ist die aktuelle Basislösung zulässig und es findet der Übergang zum primalen Simplex-Algorithmus statt. Ist dies nicht der Fall, wie in unserem Beispiel Minus 24 und Minus 4, markieren wir die Zeile mit dem kleinsten bi, in unserem Fall Minus 24. Damit haben wir auch schon unsere Pivotzeile gefunden!
Dualer Simplex – Zweiter Schritt:
Als zweites wählen wir die Pivotspalte s. Dazu berechnest du für jede Spalte cj/azj, indem du jedes Element aus der Zielfunktionszeile durch das jeweilige Element in der Pivotzeile teilst. Hier markierst du die Spalte mit dem größten, negativen Quotienten. In unserem Fall also Minus 1. Das Pivotelement azs ist das, wo sich die Pivotzeile und -spalte schneiden, also Minus 2.
Dualer Simplex – Dritter Schritt:
Im dritten Schritt berechnen wir die neue Basislösung. Wir fügen fünf neue Zeilen hinzu und beschriften die Basisvariablenzeilen. Dabei ersetzen wir die Basisvariable  in der Pivotzeile mit der Nichtbasisvariable
in der Pivotzeile mit der Nichtbasisvariable  .
.
Jetzt schaffen wir in der Spalte der neuen Basisvariable einen Einheitsvektor durch Transformation. Die neue Basisvariable soll den Wert 1 bekommen. Dazu wird die Pivotzeile 2 durch das Pivotelement „Minus 2“ geteilt. Für den Rest der Zeile erhalten wir damit:
Für die übrigen Zeilen wird die umgewandelte Pivotzeile so multipliziert und zur jeweiligen Zeile hinzuaddiert, dass eine Null im Einheitsvektor entsteht. Damit also in Zeile 5 im Einheitsvektor eine Null entsteht, muss die Zeile 6 zwei Mal zur Zeile 1 addiert werden. Diese Rechnung gilt natürlich wieder für jedes Element der Zeile.
Analog berechnen wir für die anderen Zeilen:
Damit hast du jetzt eine Iteration geschafft und wir können uns um die zweite Iteration kümmern.
Dualer Simplex – Zweite Iteration:
Da wir noch negative rechte Seiten haben, müssen wir weiter iterieren. Für die nächste Iteration müssen wir wieder das Pivotelement ermitteln. Diesen Schritt wollen wir noch gemeinsam machen und erhalten das Pivotelement Minus 2.
Den Rest der Iteration haben wir bereits ausgefüllt.
Du siehst: es gibt keine negativen rechten Seiten mehr. Das bedeutet, dass wir jetzt mit dem primalen Simplex weitermachen können, um zur optimalen Lösung zu kommen. Normalerweise…Wenn du bereits ein wenig mit dem primalen Simplex geübt hast, siehst du sofort, dass in der F-Zeile, bis auf den Zielfunktionswert „Minus 32“ keine negativen Einträge mehr vorhanden sind und wir bereits die optimale Lösung besitzen. Du kannst diese in der b-i-Spalte ablesen.
Alle Nichtbasisvariablen, die sich jetzt in der Basisvariablenspalte befinden, also  und
und  , treten in der Lösung auf.
, treten in der Lösung auf.  erhält deshalb den Wert null. Die Lösung lautet damit: x* gleich 12, 4, 0. So ergibt sich der Zielfunktionswert zu: F* gleich 32. Der duale Simplex Algorithmus ist damit abgeschlossen.
erhält deshalb den Wert null. Die Lösung lautet damit: x* gleich 12, 4, 0. So ergibt sich der Zielfunktionswert zu: F* gleich 32. Der duale Simplex Algorithmus ist damit abgeschlossen.
Alternative Lösung:
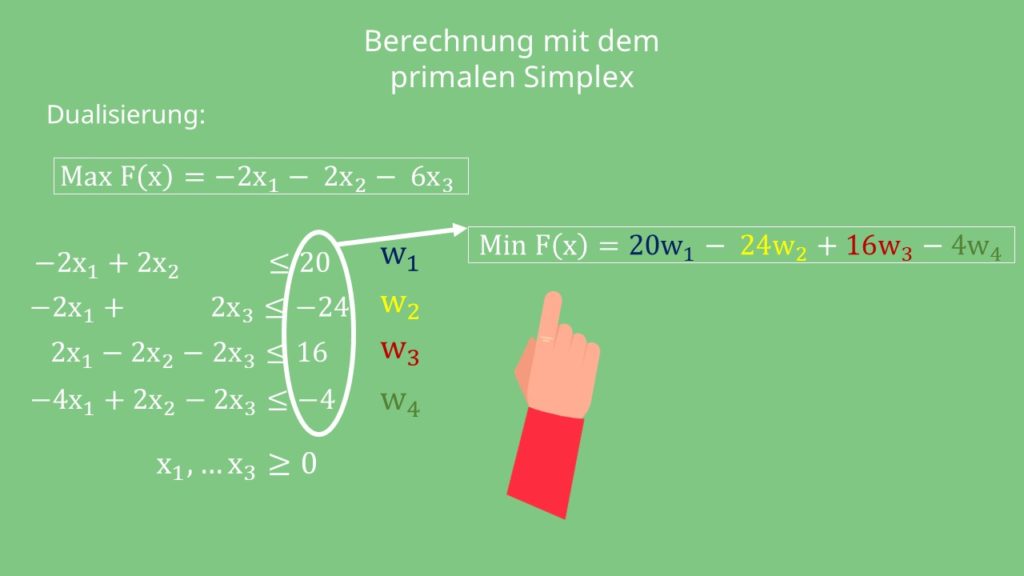
Übrigens: Man braucht für dieses Beispiel nicht unbedingt den dualen Simplex. Du hättest das Beispiel auch direkt mit dem primalen Simplex berechnen können und die gleiche Lösung herausbekommen. Dafür musst du das Gleichungssystem allerdings vorher dualisieren, um die rechten negativen Seiten wegzubekommen.
Denn diese müssen positiv sein. Was dualisieren heißt, schauen wir uns jetzt an: Zu jeder Nebenbedingung i des primalen Modells gibt es jetzt eine Dualvariable wi. Das bedeutet, dass die rechten Seiten zu den Zielfunktionskoeffizienten des dualen Modells werden. Damit ergibt sich die neue Zielfunktion zu:
Du siehst, dass Maximierungen im primalen Modell zu Minimierungen im dualen Modell werden und umgekehrt. Zu jeder Variable xj gibt es nun eine Nebenbedingung j im dualen Modell. Für  beispielsweise erhalten wir die neue Nebenbedingung:
beispielsweise erhalten wir die neue Nebenbedingung:
Du überträgst also einfach die Faktoren vor jedem  in eine neue duale Nebenbedingung. Für die rechte Seite verwendest du den Faktor vor
in eine neue duale Nebenbedingung. Für die rechte Seite verwendest du den Faktor vor  in der Zielfunktion, also -2. Analog erhalten wir die anderen Nebenbedingungen zu:
in der Zielfunktion, also -2. Analog erhalten wir die anderen Nebenbedingungen zu:
Jetzt gibt es noch ein einige weitere Regeln, die du beachten musst. Die i-te Nebenbedingung im primalen Modell mit einem kleiner-gleich-Zeichen besagt, dass die i-te Dualvariable größer gleich Null ist. Also, da die erste Nebenbedingung ein kleiner-Zeichen hat, ist die Dualvariable  größer gleich Null. Da hier alle Nebenbedingungen ein kleiner-gleich-Zeichen haben, sind auch alle Dualvariablen größer gleich Null.
größer gleich Null. Da hier alle Nebenbedingungen ein kleiner-gleich-Zeichen haben, sind auch alle Dualvariablen größer gleich Null.
Die i-te Nebenbedingungen im primalen Problem mit einem Gleichheitszeichen besagt, dass die i-te Dualvariable Element der reellen Zahlen ist. Da wir in unserem Beispiel keine Nebenbedingung mit einem Gleichheitszeichen haben, betrifft uns diese Regel nicht. Die primal i-te Variable, die größer oder gleich Null ist, besagt, dass die i-te Nebenbedingung im dualen Problem ein größer- oder gleich-Zeichen bekommt. In unserem Fall bedeutet das, dass alle dualen Nebenbedingungen 1 bis 3 ein größer-gleich-Zeichen bekommen, da alle Variablen  bis
bis  größer Null sind. Sollte eine i-te Variable Element der rellen Zahlen sein, würde die i-te Nebenbedingung im dualen System ein Gleichheitszeichen bekommen.
größer Null sind. Sollte eine i-te Variable Element der rellen Zahlen sein, würde die i-te Nebenbedingung im dualen System ein Gleichheitszeichen bekommen.
Auch diesen Fall haben wir in unserem Beispiel nicht. Bei einem Gleichungssystem mit minimierender Funktion, wendest du die Regeln einfach rückwärts an. Super, jetzt haben wir die Dualform. Wie du bereits im Video Optimierungsmodelle gelernt hast, müssen wir diese jetzt noch transformieren, damit wir eine zu maximierende Zielfunktion bekommen. Das duale, transformierte Gleichungssystem können wir dann mit dem primalen Simplex lösen und erhalten das gleiche Ergebnis wie beim dualen Simplex.