Prim Algorithmus
Der minimale Spannbaum eines Graphen – was das ist, und wie man diesen mit dem Algorithmus von Prim erstellt, zeigen wir dir in diesem Beitrag!
Inhaltsübersicht
Algorithmus von Prim – minimaler Spannbaum
Der Algorithmus von Prim berechnet, wie der Kruskal-Algorithmus , den minimalen Spannbaum eines zusammenhängenden , gewichteten Graphen . Du weißt nicht was das ist? Kein Problem! Ein Spannbaum ist dann minimal, wenn er alle Knoten eines Graphen enthält. Zudem darf kein anderer Baum existiert, der die Knoten zu geringeren Kosten verbinden kann.
Ablauf des Prim Algorithmus
Aber wie berechnet man denn jetzt mit dem Prim-Algorithmus den minimalen Spannbaum?
Als erstes erstellen wir einen neuen Graphen . Dazu suchst du dir einen beliebigen Startknoten aus dem alten Graphen. Es ist egal welchen du zuerst auswählst. Am Ende wird sowieso jeder Knoten im minimalen Spannbaum enthalten sein.
Bis alle Knoten im neuen Graphen abgebildet sind wählst du immer genau die Kante mit den geringsten Kosten, die einen neuen Knoten mit dem Graphen verbindet. Dieses Schema wird wiederholt, bis der neue Graph alle Knoten des alten enthält.
Vielleicht ist dir bereits aufgefallen, dass der Algorithmus immer die aktuell beste Möglichkeit, nicht aber die global beste betrachtet. Aus diesem Grund fällt er in die Klasse der Greedy-Algorithmen . Was diese sind erklären wir dir in einem kurzen Video.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispiel für Prims Algorithmus
Schauen wir uns nun den Prim-Algorithmus an einem Beispiel an.
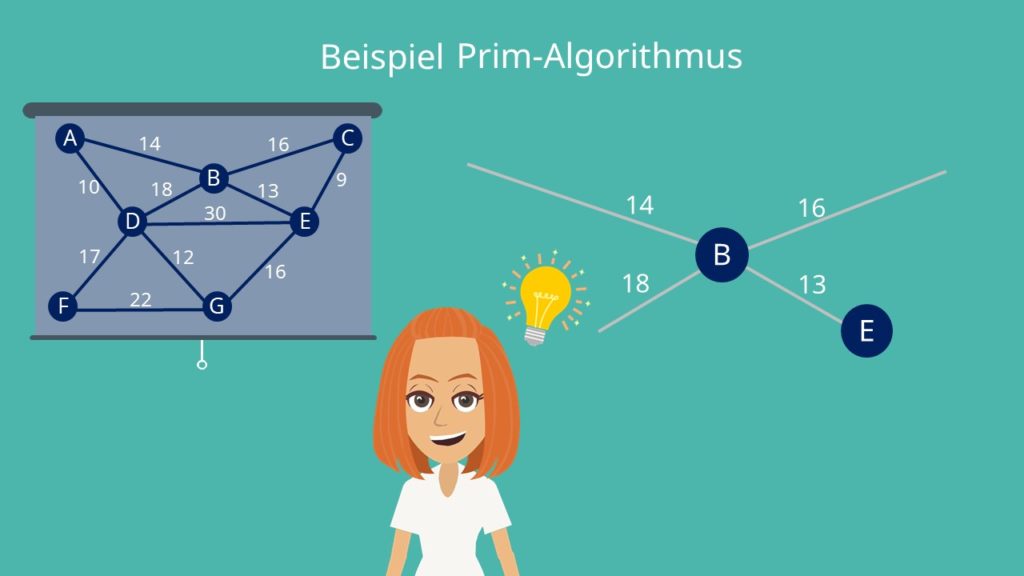
Als Startknoten wählen wir einfach Knoten B. Jeder andere wäre aber ebenfalls völlig in Ordnung.
Werfen wir nun einen Blick auf alle Kanten, die im ursprünglichen Graphen von B ausgehen. Wir wählen die kürzeste, also die Kante von B zu E mit den Kosten von 13 und fügen sie zu unserem Graphen hinzu. Perfekt!
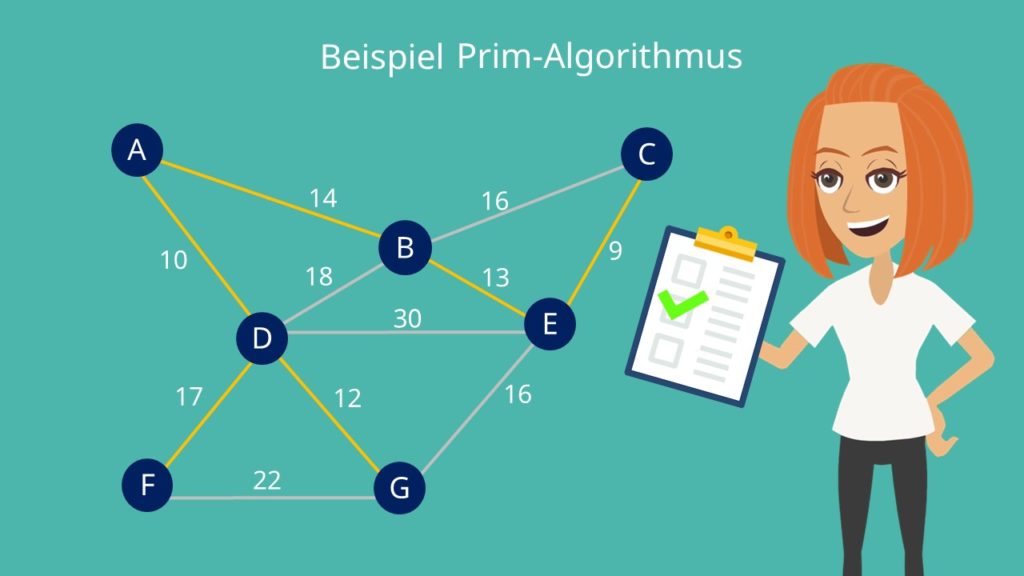
Diesen Schritt wiederholen wir. So kannst du erkennen, dass die kürzeste Kante, die einen neuen Knoten mit einem der Knoten unseres Teilgraphen verbindet, die Kante von E nach C ist. Auch diese fügen wir also hinzu.
Diese Schritte wiederholen wir so lange, bis wir alle Knoten in unserem neuen Graphen eingefügt haben.
Wie du siehst, haben wir nun alle Knoten miteinander verbunden. Einige Kanten des alten Graphen werden nicht genutzt. Diese sind überflüssig also lassen wir sie weg. Somit haben wir nun unseren minimalen Spannbaum gefunden.
Jetzt kannst du mithilfe des Prim-Algorithmus den minimalen Spannbaum eines beliebigen Graphen berechnen. Super simpel, oder?
Unterschied zwischen Prim und Kruskal Algorithmus
Der Unterschied zum Kruskal-Algorithmus liegt darin, wie der minimale Spannbaum aufgebaut wird. Beim Prim-Algorithmus wird mit einem Knoten gestartet. Von diesem ausgehend wird nach und nach ein Teilgraph gebildet. Der Kruskal-Algorithmus hingegen sortiert die Kanten nach den Gewichten und fügt sie in aufsteigender Reihenfolge hinzu.
Pseudocode Prim Algorithmus
Wie der Prim-Algorithmus implementiert werden kann, wird an diesem einfachen Pseudocode klar:
Initialisierung
Ausgangsgraph G
Erstelle neuen Graphen MST
Wähle Startknoten von G und füge ihn in MST hinzu
Iterationen
solange Knoten MST ≠ Knoten G
finde Kante mit min. Knotengewicht die mit Knoten aus MST verbunden ist und neuen Knoten zu MST hinzufügt
füge neue Kante zu MST hinzu
füge neuen Knoten zu MST hinzu
Output:
MST ist der Minimale Spannbaum von G