Ungarische Methode
Du wolltest immer schon wissen wie du möglichst fair zuordnen kannst wer wann in den Urlaub fahren darf? Wir erklären dir wie du Zuordnungsprobleme mithilfe der ungarischen Methode ganz einfach lösen kannst!
Inhaltsübersicht
Lösung linearer Zuordnungsprobleme: Ungarische Methode
Die Ungarische Methode, die auch als Kuhn-Munkres-Algorithmus bezeichnet wird, ist ein Algorithmus der gewichtete Zuordnungsprobleme löst.
Zwischen zwei Gruppen von Objekten soll eine eindeutige Zuordnung hergestellt werden. Zu beachten ist außerdem, dass entweder die Gesamtkosten der Zuordnung minimiert werden oder der Gesamtgewinn zu maximieren ist.
Allgemeiner Ablauf und Vorgehen bei der Ungarischen Methode
Allgemein läuft die Ungarische Methode folgendermaßen ab:
Zuerst findet eine Reduktion der Ausgangsmatrix statt. Zum einen eine Reduktion der Spaltenelemente um das Spaltenminimum, zum anderen eine zeilenweise Reduktion um das jeweilige Zeilenminimum.
Dann wird die Zuordnung vorgenommen. Dafür suchst du dir zuerst die Zelle mit einer Null, bei der sonst in der Zeile oder Spalte keine weitere Null zu finden ist. Bei den weiteren Zuordnungen musst du darauf achten, dass jede Spalte und jede Zeile nur genau eine Zuordnung aufweist.
Sind n Zuordnungen gefunden ist die Lösung optimal.
Das klingt jetzt erstmal ganz schön komplex, aber eigentlich ist das alles gar nicht so schwer.
-
Reduktion der Ausgangsmatrix
- Spaltenweise Reduktion
- Zeilenweise Reduktion
-
Zuordnung
- Jede Spalte und jede Zeile dürfen nur eine Zuordnung aufweisen
- Genau n Zuordnungen gefunden? -> Lösung ist optimal
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispiel zur Ungarischen Methode
Wir schauen uns am besten ein ganz einfaches Beispiel für ein Zuordnungsproblem an.
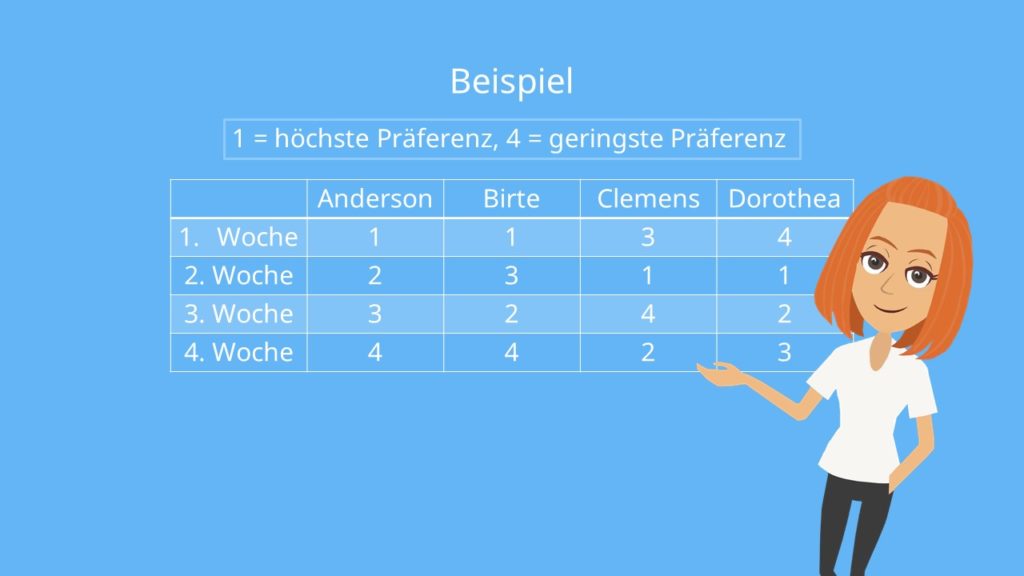
4 Kollegen planen ihre Arbeitsaufteilung für den Sommer. Jeder von Ihnen möchte im Juli eine Woche in den Urlaub fahren. Doch es werden immer mindestens 3 von Ihnen in der Arbeit gebraucht.
Also erstellen sie eine Matrix, in die sie ihre Präferenzen eintragen. Die Spalten stehen für die jeweiligen Mitarbeiter und die Zeilen für die Wochen 1 bis 4 im Juli. 1 beutet die höchste Präferenz, 4 die geringste.
Reduktion der Spaltenelemente um das Spaltenminimum
Im ersten Schritt werden die Spaltenelemente um das jeweilige Spaltenminimum reduziert. Für die Spalte Anderson bedeutet das konkret: Das Spaltenminimum 1 wird ganz einfach von den Spalteneinträgen abgezogen.
Für alle anderen Spalten wird analog vorgegangen.
Optimale Zuordnung
Nun beginnst du mit der Zuordnung. Das funktioniert so ein bisschen wie Sudoko.
Zuerst suchst du dir die Zeile oder Spalte, die nur eine Null enthält und umrandest die entsprechende Zelle. Von hier ausgehend kannst du jetzt ermitteln, welche weiteren Nullen du umranden musst. Dabei darf jeweils in jeder Zeile und Spalte nur ein Kästchen markiert sein.
Sehr gut! Jetzt kannst du ganz einfach ablesen welcher Kollege in welcher Woche in den Urlaub darf und mit welcher Präferenz er die jeweilige Woche bewertet hat:
Anderson zum Beispiel hat in der ersten Woche frei. Das war auch seine erste Wahl. Birte muss in der Dritten Woche nicht arbeiten – das war ihre zweite Präferenz.
Super! Das ging doch ganz einfach!
Jetzt weist du wie du dich ganz einfach mit deinen Geschwistern einigen kannst wer wann dafür verantwortlich ist die Blumen zu gießen, wenn eure Eltern im Urlaub sind.