Big-M-Methode / M-Methode
Du bist dir nicht mehr sicher wie man bei der Big-M-Methode (kurz: M-Methode) vorgehen muss? Keine Sorge! In diesem Beitrag erklären wir dir die M-Methoden Schritt für Schritt anhand einer Beispielrechnung.
Inhaltsübersicht
Big-M-Methode / M-Methode: Erklärung und Beispielrechnung
Bei der Big-M-Methode ist es möglich auf die optimale Lösung eines Gleichungssystems zu kommen, ohne dass sich eine Einheitsmatrix unter den Schlupfvariablen bilden muss. Jedoch gilt dabei wieder, dass die rechten Seiten nichtnegativ sein müssen, das System in der Normalform vorliegt, und die Zielfunktion maximierend ist. In unserem Beispiel ist die M-Methode sinnvoll. Hier haben wir nämlich größer gleich- und kleiner gleich- Zeichen. Wenn wir dieses Gleichungssystem jetzt in die Normalform bringen, siehst du, dass die Schlupfvariablen nicht alle positiv sind und wir es nicht mit dem primalen und dem dualen Simplex lösen können.
Beispiel: Big-M-Methode
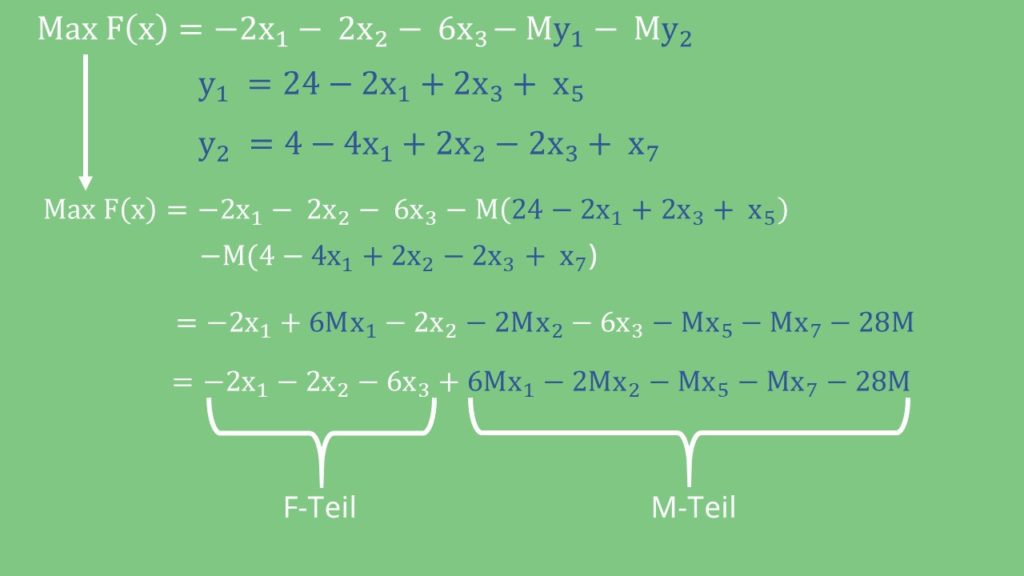
In den Zeilen, die einen negative Schlupfvariable haben, werden künstliche Variablen yn eingeführt.
Diese künstlichen Variablen werden in der Zielfunktion mit einer sehr hohen Zahl M multipliziert.
Nun musst du die Nebenbedingungen nach  und
und  umstellen. Das setzt du jetzt in die Zielfunktion ein und wir erhalten:
umstellen. Das setzt du jetzt in die Zielfunktion ein und wir erhalten:
Dann vereinfachst du diesen Term, so weit es geht. Nachdem wir alle Komponenten sortiert haben, kannst du dann einen F-Teil und einen M-Teil ablesen.
Damit haben wir den ersten der Teil Big-M-Methode erledigt und können zu unserem Gleichungssystem zurückkehren.
Dieses können wir jetzt wieder in unser Tableau übertragen. Wie du siehst, gibt es im Tableau eine zusätzliche M-Zeile unter der F-Zeile und Spalten für jede künstliche Variable y. In die F-Zeile fügst du den F-Teil aus der Zielfunktion ein. In die M-Zeile schreibst du den Strafkosten-M-Teil der Zielfunktion . Beachte dabei, dass die Werte wie bisher auch mit umgekehrtem Vorzeichen eingesetzt werden. Der b i-Wert der M Zeile behält sein Vorzeichen, da er zuvor auf die andere Seite der Gleichung gebracht werden muss. So, kommen wir nun zur ersten Iteration!
Als Pivotspalte wählst du aus der M-Zeile die kleinste Eintragung. In unserem Fall Minus 6M. Für die Pivotzeile berechnest du bi/aiz. In Zeile 4 beispielsweise teilen wir 4 durch 4 und erhalten 1. Für die restlichen Quotienten erhalten wir:
Wir wählen jetzt wieder den kleinsten Quotienten, also in unserem Fall die 1. Unser erstes Pivotelement ist damit gleich 4. Um mit der Big-M-Methode fortzufahren, fügen wir wieder neue Zeilen hinzu.
Jetzt nimmst du die Nichtbasisvariable aus der Pivotspalte  als neue Basisvariable auf und eliminierst damit die künstliche Variable
als neue Basisvariable auf und eliminierst damit die künstliche Variable  . In der Spalte des Pivotelements schaffst du einen Einheitsvektor. Dabei wird auch die F- und die M-Zeile miteinbezogen. Für die Big-M-Methode ergibt sich folgende Iteration:
. In der Spalte des Pivotelements schaffst du einen Einheitsvektor. Dabei wird auch die F- und die M-Zeile miteinbezogen. Für die Big-M-Methode ergibt sich folgende Iteration:
Die  Spalte wird dabei direkt eliminiert, da wir sie ja durch das
Spalte wird dabei direkt eliminiert, da wir sie ja durch das  ersetzt haben. Merke dir am besten, dass alle y, die nicht mehr in der linken Spalte stehen, gestrichen werden können. Du fährst jetzt solange fort, bis alle künstlichen Variablen entfernt sind. Bei uns ist das noch die Variable
ersetzt haben. Merke dir am besten, dass alle y, die nicht mehr in der linken Spalte stehen, gestrichen werden können. Du fährst jetzt solange fort, bis alle künstlichen Variablen entfernt sind. Bei uns ist das noch die Variable  . Du siehst, dass dafür eine weitere Iteration ausreicht. Wir haben dir hier das nächste Tableau bereits ausgefüllt – die Berechnung erfolgt analog zur ersten Iteration.
. Du siehst, dass dafür eine weitere Iteration ausreicht. Wir haben dir hier das nächste Tableau bereits ausgefüllt – die Berechnung erfolgt analog zur ersten Iteration.
Jetzt ist die Lösung optimal, da keine negativen Eintragungen mehr in der F-Zeile vorhanden sind, können wir mit der M-Methode abschließen. Ist das nicht der Fall, machst du einfach mit dem primalen Simplex weiter. Die optimale Lösung ergibt sich damit zu:
x* = (12, 22, 0), F* = 68