Impulsantwort
In diesem Artikel geben wir dir einen vollständigen Überblick zur Impulsantwort. Neben grundlegenden Informationen zur Impulsfunktion erfährst du auch, wie du die Impulsantwort im Zeit- und Bildbereich berechnest und wie du die Endwertsätze der Laplacetransformation richtig anwendest. Schau dir unser Video dazu an, in dem wir das Wichtigste in unter fünf Minuten verständlich erklären.
Inhaltsübersicht
Impulsantwort
Als Impulsantwort wird das Ausgangssignal eines Systems bezeichnet, welches mit einem Impuls angeregt wurde.
 . Das Ausgangssignal xa(t) entspricht der Impulsantwort.
. Das Ausgangssignal xa(t) entspricht der Impulsantwort.Die Impulsantwort wird häufig auch als Gewichtsfunktion bezeichnet und wird mit g(t) abgekürzt.
Impulsfunktion
Die Impulsfunktion  beschreibt einen unendlich hohen und unendlich kurzen Impuls an dem Zeitpunkt t ist gleich 0. Dieser Impuls wird auch als Dirac-Impuls bezeichnet.
beschreibt einen unendlich hohen und unendlich kurzen Impuls an dem Zeitpunkt t ist gleich 0. Dieser Impuls wird auch als Dirac-Impuls bezeichnet.
Im Koordinatensystem wird die unendliche Höhe durch einen Pfeil symbolisiert. Die Länge des Pfeils gibt dabei die Fläche an, die der Impuls mit der x-Achse einschließt. Eine wichtige Eigenschaft, ist, dass die Fläche unter dem Impuls gleich 1 ist.

Das beutet in diesem Fall, dass auch die Laplacetransformierte der Impulsfunktion gleich 1 ist.

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Impulsantwort berechnen im Zeitbereich
Im Zeitbereich lässt sich die Impulsantwort mithilfe des Faltungsintegrals berechnen, dieses sieht dann so aus:

 entspricht der Impulsfunktion
entspricht der Impulsfunktion
 entspricht der Übertragungsfunktion des PT1 Systems im Zeitbereich
entspricht der Übertragungsfunktion des PT1 Systems im Zeitbereich
Die Impulsantwort entspricht also der Übertragungsfunktion des Systems im Zeitbereich.
Impulsantwort berechnen im Bildbereich
Die Übertragungsfunktion eines PT1-Systems lautet allgemein:

Die Faltung im Zeitbereich entspricht einer Multiplikation im Bildbereich.
Für die Impulsantwort im Bildbereich ergibt somit aus dem Produkt der Impulsfunktion und der Übertragungsfunktion des Systems:
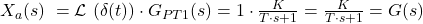
Anfangs- und Endwerte der Impulsantwort
Um Aussagen über die Parameter des Systems treffen zu können, bietet es sich an, die Anfangs- und Endwerte der Impulsantwort zu bestimmen. Dafür wird der Endwertsatz der Laplacetransformation verwendet. Für den Anfangswert  ergibt sich:
ergibt sich:

Für den Endwert  ergibt sich:
ergibt sich:

Rücktransformation der Impulsantwort in den Zeitbereich [[ jump_to_video 04:07]]
Für die Rücktransformation vom Bild- in den Zeitbereich kann häufig anstatt der Laplacerücktransformation eine Korrespondenztabelle verwendet werden. Mit ihrer Hilfe ergibt sich hier:

Grafische Darstellung der Impulsantwort [[ jump_to_video 04:35]]
Mit den Erkenntnissen aus dem Endwertsatz und Rücktransformation lässt sich die Impulsantwort eines PT1 Systems grafisch darstellen:
Zu erkennen sind die ermittelten Anfangs- und Endwerte aus dem Endwertsatz der Laplacetransformation für  und
und  . Dazwischen folgt die Impulsantwort eines PT1-Glieds einer abfallenden e-Funktion.
. Dazwischen folgt die Impulsantwort eines PT1-Glieds einer abfallenden e-Funktion.




