Stabilitätskriterium nach Hurwitz
Du möchtest wissen, welche Stabilitätskriterien die Regelungstechnik nutzt, wenn sie Systeme beurteilt? Dann ist das Hurwitz-Kriterium deine erste Etappe!
Inhaltsübersicht
Das Stabilitätskriterium nach Hurwitz mit Beispiel
Der deutsche Mathematiker Adolf Hurwitz beschäftigte sich nicht nur mit der Zahlentheorie, sondern auch mit dem Bereich der Funktionentheorie. Aus seinen Überlegungen ergibt sich ein Stabilitätskriterium für Systeme, das auf der Betrachtung eines besonderen Polynoms basiert.Ein Polynom ist ein mathematischer Ausdruck, der Vielfache von Potenzen einer Variable aufsummiert. Merke dir, dass du das folgende Verfahren nur für Regelkreise anwenden kannst, die keine Totzeitelemente besitzen!
Um zu prüfen, ob das System asymptotisch stabil ist, muss es eine Übertragungsfunktion G(s) besitzen, die folgende Form aufweist:
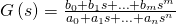
Setzt du den Nenner ( ) der Übertragungsfunktion gleich Null, erhältst du das charakteristische Polynom p(s):
) der Übertragungsfunktion gleich Null, erhältst du das charakteristische Polynom p(s):

Es wird vorausgesetzt, dass  größer Null ist. Ist dies nicht der Fall, musst du das Polynom mit minus Eins durchmultiplizieren.
größer Null ist. Ist dies nicht der Fall, musst du das Polynom mit minus Eins durchmultiplizieren.
Damit das System asymptotisch stabil ist, gibt es die notwendige Bedingung, dass alle Koeffizienten  des Polynoms existieren und positiv sein müssen.
des Polynoms existieren und positiv sein müssen.  für i=1,…,n
für i=1,…,n
Ist diese erste Bedingung nicht erfüllt, kann das System schon nicht mehr stabil sein!
Hinreichende Bedingungen
Jetzt folgen sogenannte hinreichende Bedingungen. Falls ein asymptotisch stabiles System vorliegt, werden auch diese erfüllt. Das kleine n gibt dabei die Ordnung eines Systems an, welche du an der höchsten Potenz von s im Polynom ablesen kannst. Liegt beispielsweise nichts Höheres als 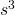 im Polynom vor, so ist es ein System dritter Ordnung.
im Polynom vor, so ist es ein System dritter Ordnung.
Um diese Bedingungen aufzustellen, bedient man sich einer (nxn)-Matrix, die wir  nennen. Auf der Hauptdiagonalen trägst du alle Koeffizienten
nennen. Auf der Hauptdiagonalen trägst du alle Koeffizienten  des Polynoms auf. In jeder Spalte werden die Koeffizienten mit fallendem Index i aufgetragen: Koeffizienten, deren Index größer oder kleiner als n ist, ersetzt du einfach durch eine Null. Der nächste Schritt ist dir sicher noch aus dem Matheunterricht bekannt: Wir bilden die linken oberen Unterdeterminanten. Dazu gehst du in die obere linke Ecke der Matrix und schreibst für die erste Determinante
des Polynoms auf. In jeder Spalte werden die Koeffizienten mit fallendem Index i aufgetragen: Koeffizienten, deren Index größer oder kleiner als n ist, ersetzt du einfach durch eine Null. Der nächste Schritt ist dir sicher noch aus dem Matheunterricht bekannt: Wir bilden die linken oberen Unterdeterminanten. Dazu gehst du in die obere linke Ecke der Matrix und schreibst für die erste Determinante  eine Eins Kreuz Eins Matrix, in der nur
eine Eins Kreuz Eins Matrix, in der nur  steht. Für die zweite Determinante, die wir
steht. Für die zweite Determinante, die wir  nennen, bilden wir eine Zwei Kreuz Zwei Matrix aus der oberen linken Ecke der Matrix: Dieses Prinzip kannst du weiterführen, je nachdem mit wie vielen Stellen deine ursprüngliche
nennen, bilden wir eine Zwei Kreuz Zwei Matrix aus der oberen linken Ecke der Matrix: Dieses Prinzip kannst du weiterführen, je nachdem mit wie vielen Stellen deine ursprüngliche  -Matrix besetzt ist und welche Ordnung das System besitzt.
-Matrix besetzt ist und welche Ordnung das System besitzt.
Die hinreichende Bedingung lautet, dass jede dieser Determinanten einen Wert größer Null haben muss!
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Berechnung einer Determinante
Dazu erinnern wir uns an die Berechnung einer Determinante, indem wir  als Beispiel verwenden:
als Beispiel verwenden:
Wir multiplizieren die obere linke Ecke mit der unteren rechten Ecke und ziehen davon das Produkt der unteren linken Ecke und der oberen rechten Ecke ab:

Der Wert, der sich daraus ergeben würde, muss größer Null sein. Hast du beispielsweise ein System dritter Ordnung vorliegen, musst du also die erste Determinante  und die zweite Determinante
und die zweite Determinante  bilden und ausrechnen, da dein höchster vorhandener Koeffizient im Polynom
bilden und ausrechnen, da dein höchster vorhandener Koeffizient im Polynom  lautet.
lautet.
Für ein System vierter Ordnung mit n gleich vier, erhältst du durch die Berechnung der Determinanten auch eine hinreichende Bedingung

die größer Null sein muss.
Auch für n=5 müssen die Determinanten positiv sein!
 und
und 
Wenn du diese Regeln in einem konkreten Beispiel anwenden und noch über den Tellerrand hinausschauen möchtest, dann sieh dir unser Übungsvideo zum Stabilitätskriterium nach Hurwitz
an.
Die erste Etappe hast du jetzt erfolgreich bestritten. Wenn du fleißig dranbleibst, dann wird die nächste auch ein Klacks!


