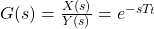Regelstrecke
Im folgenden Artikel erklären wir dir die Grundlagen zur Regelstrecke und gehen dabei auf die verschiedenen Arten von Regelstrecken ein. Für einen schnellen Überblick zum Thema, schau dir am besten unser Video an.
Inhaltsübersicht
Regelstrecke Definition
Der Eingang der Regelstrecke ist dabei die Stellgröße y(t) und ihr Ausgang die Regelgröße x(t). Der Einfluss der Stellgröße auf die Regelgröße ist dabei im Bildbereich über die Übertragungsfunktion G(s) der Regelstrecke gegeben.
Grundsätzlich wird zwischen zwei Arten von Regelstrecken unterschieden: den Regelstrecken mit und ohne Ausgleich.
Regelstrecken mit Ausgleich
Eine Regelstrecke wird als Regelstrecke mit Ausgleich bezeichnet, wenn ihr Ausgang bei gleichbleibendem Eingang einen konstanten Wert anstrebt. Konkret handelt es sich bei Regelstrecken, die keinen I-Anteil haben, um Regelstrecken mit Ausgleich. Das beinhaltet alle P-, PD-, PTn– und Totzeitstrecken.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Regelstrecken ohne Ausgleich
Regelstrecken ohne Ausgleich erreichen bei gleichbleibendem Eingang keinen konstanten Endwert am Ausgang. Beispielsweise ist ihr Ausgang bei Anregung durch einen Sprung stetig steigend. Es handelt sich dabei um Regelstrecken mit integrierendem Verhalten. Dazu zählen unter anderem reine I-Regelstrecken, ITn Regelstrecken, PID-Strecken.
Übertragungsfunktion einer Regelstrecke
Die Übertragungsfunktion einer Regelstrecke stellt das Verhältnis von ihrem Ausgang zu ihrem Eingang im Bildbereich dar und wird mit G(s) bezeichnet. Die Übertragungsfunktion beschreibt also das Verhältnis  der Regelgröße x zur Stellgröße y.
der Regelgröße x zur Stellgröße y.
In der Regel handelt es sich bei G(s) um eine gebrochen-rationale Funktion mit einem Polynom im Zähler und im Nenner. Die Pol- und Nullstellen dieser Polynome geben darüber Auskunft, um was für eine Art von Regelstrecke es sich handelt.

Übertragungsfunktion mathematisch bestimmen
Mathematisch kann die Übertragungsfunktion einer Regelstrecke aus deren Differenzialgleichung bestimmt werden. Das Vorgehen wird zum Beispiel in unserem Artikel zum PT1-Glied demonstriert. Grundsätzlich wird dafür zunächst die Differenzialgleichung der Regelstrecke laplacetransformiert und anschließend das Verhältnis von Ausgangs- und Eingangsgröße gebildet. Weiter unten in diesem Artikel findet sich eine Übersicht der gängigen Regelstrecken mit ihren jeweiligen Übertragungsfunktionen und Differenzialgleichungen.
Übertragungsfunktion in der Praxis bestimmen
In der Praxis kann die Übertragungsfunktion einer unbekannten Regelstrecke gewonnen werden, indem auf die Strecke ein bekanntes Testsignal (z.B. Einheitssprung) gegeben wird und gleichzeitig deren Ausgang gemessen wird. Das gemessene Ausgangssignal entspricht in diesem Fall der Sprungantwort im Zeitbereich und gibt Aufschluss über die Übertragungsfunktion der Regelstrecke.
Alternativ ist es möglich, die Übertragungsfunktion über den Frequenzgang zu bestimmen. Dafür werden auf das System am Eingang sinusförmige Signale unterschiedlicher Frequenz gegeben und gleichzeitig der Ausgang betrachtet. Aus dem Verhältnis des Ein- und Ausgangssignals ist es dann möglich, das Bodediagramm , also den Amplitudengang und Phasengang des Systems, zu erstellen und daraus die Übertragungsfunktion zu ermitteln.
Lineare Regelstrecken
Kommen wir nun zu den linearen Regelstrecken beziehungsweise zu P-Regelstrecke.
P-Regelstrecke
Eine P-Regelstrecke entspricht einem P-Glied und weist dementsprechend identische Eigenschaften auf. Die Ausgangsgröße der P-Regelstrecke ist also proportional zu ihrem Eingang.
Ihre Differenzialgleichung lautet:

Die Übertragungsfunktion ergibt sich entsprechend als:

PT1-Regelstrecke
Eine PT1-Regelstrecke, auch als System 1. Ordnung bezeichnet, wird durch ein PT1-Glied beschrieben. Das Ausgangssignal erreicht seinen Endwert also nicht sofort, sondern erst nach einer Verzögerung.
Differenzialgleichung:
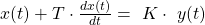
Übertragungsfunktion:

Für eine genauere Betrachtung inklusive der Sprungantwort und des Bodediagramms schau dir unseren Beitrag zum PT1 Glied an.
PT2-Regelstrecke
Bei einer PT2-Regelstrecke handelt es sich um zwei in Reihe geschaltete PT1-Glieder. Systeme mit PT2 Verhalten werden auch als Systeme 2. Ordnung bezeichnet.
Differenzialgleichung:

Übertragungsfunktion:

D wird hierbei als Dämpfung und als Eigenkreisfrequenz bezeichnet.
Totzeitglied
In der Praxis ist das Totzeitglied häufig ein Bestandteil einer Regelstrecke und tritt in der Regel in Verbindung mit anderen Übertragungsgliedern auf. Es beschreibt häufig die Verzögerungen, die durch Signallaufzeiten beziehungsweise Transportvorgänge auftreten.
Differenzialgleichung:

Übertragungsfunktion: