Sprungantwort
In diesem Artikel möchten wir dir einen Überblick über die Sprungantwort geben. Dazu gehen wir auf die Definition der Sprungantwort und Sprungfunktion im Zeit- und Bildbereich ein und zeigen dir die Berechnung am Beispiel eines PT1-Gliedes. Schau dir am besten direkt unser Video an, um eine Zusammenfassung der wichtigsten Punkte zu erhalten.
Inhaltsübersicht
Sprungantwort und Sprungfunktion
Die Systemantwort, also das Ausgangssignal xa(t) eines mit einem Sprung angeregten System, wird als Sprungantwort bezeichnet. Sie wird in der Regel mit h(t) abgekürzt
Das Sprungsignal kann dabei, durch die Sprungfunktion 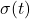 bzw. den Einheitssprung 1(t) beschrieben werden. Wird das System mit dem Einheitssprung angeregt, so wird die Sprungantwort auch als Übergangsfunktion bezeichnet.
bzw. den Einheitssprung 1(t) beschrieben werden. Wird das System mit dem Einheitssprung angeregt, so wird die Sprungantwort auch als Übergangsfunktion bezeichnet.
Das bedeutet in diesem Fall ist das Eingangssignal gleich der Sprungfunktion:

Sprungfunktion: Mathematische Definition im Zeitbereich
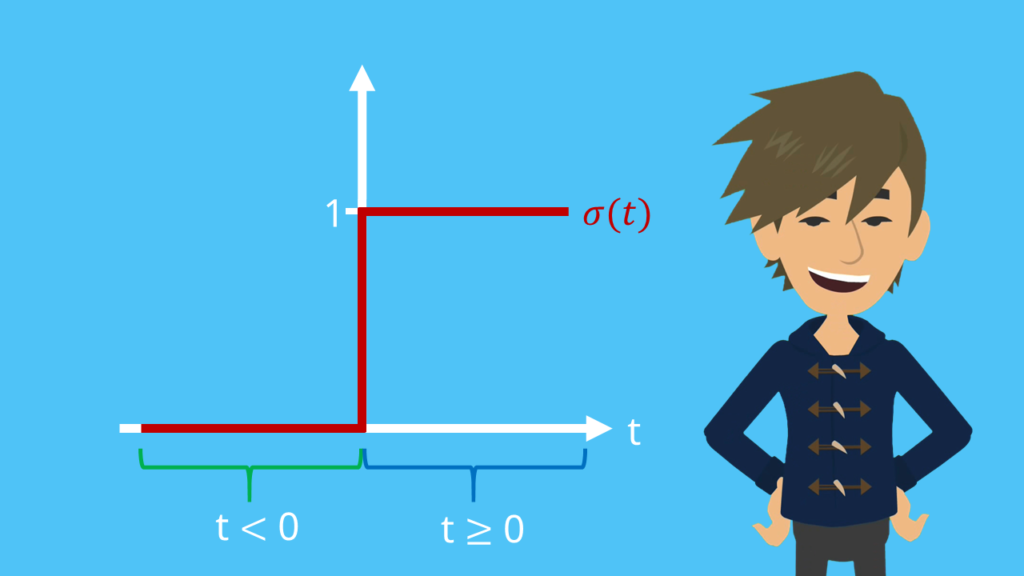
Die Sprungfunktion oder auch Einheitssprungfunktion ist im Zeitbereich abschnittsweise definiert.

Für Zeitpunkte t kleiner 0 ist sie 0.
Für Zeitpunkte t größer gleich 0 nimmt sie den Wert 1 an.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Zusammenhang zwischen Impulsfunktion und Sprungfunktion im Zeitbereich
Eine weitere Möglichkeit die Sprungfunktion zu definieren, ist durch zur Hilfenahme der Impulsfunktion
 .
.
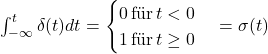
Die Sprungfunktion entspricht also dem Integral der Impulsfunktion.
Sprungfunktion im Bildbereich
Laplacetransformierte der Sprungfunktion

Zusammenhang zwischen Sprungfunktion und Impulsfunktion im Bildbereich
Eine Möglichkeit die Sprungfunktion im Bildbereich darzustellen, ist den Zusammenhang zur Impulsfunktion zu nutzen. Die Laplacetransformierte der Impulsfunktion  ergibt sich als:
ergibt sich als:

Die Sprungfunktion erhalten wir aus der Impulsfunktion durch Integration. Das Integrieren im Zeitbereich entspricht der Multiplikation mit  . Damit ergibt sich folgender Zusammenhang.
. Damit ergibt sich folgender Zusammenhang.

Sprungantwort berechnen
Das Ausgangssignal xa(t) eines mit einem Sprung angeregten Systems, wird als Sprungantwort bezeichnet. Handelt es sich bei dem Eingangsignal um einen Sprung der Höhe 1, so wird die Sprungantwort auch als Übergangsfunktion bezeichnet.
Abgekürzt wird die Sprungantwort in der Regel mit h(t). Der allgemeine Zusammenhang zwischen Anregung  (Eingangssignal) und Systemantwort
(Eingangssignal) und Systemantwort 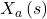 (Ausgangssignal) ergibt sich im Bildbereich als:
(Ausgangssignal) ergibt sich im Bildbereich als:

G(s) entspricht hier der Übertragungsfunktion des Systems.
Für die Sprungantwort ergibt sich damit:

Sprungantwort PT1-System im Bildbereich
Die Sprungantwort eines PT1 Systems im Bildbereich ergibt sich als:

mit der Übertragungsfunktion  eines PT1-Systems folgt:
eines PT1-Systems folgt:

Anfangs -und Endwerte der Sprungantwort
Für die Ermittlung der Anfangs -und Endwerte im Bildbereich, wird der Endwertsatz der Laplacetransformation genutzt.
Für den Anfangswert  ergibt sich:
ergibt sich:

Für den Endwert  folgt:
folgt:

Anfangs -und Endsteigung der Sprungantwort
Für die Ermittlung der Anfangs -und Endsteigung muss die betrachtete Funktion zunächst differenziert und anschließend der Endwertsatz der Laplacetransformation angewandt werden. Der Differenziation im Zeitbereich entspricht im Bildbereich einer Multiplikation mit s.
Für die Anfangssteigung  ergibt sich daher:
ergibt sich daher:

Für die Endsteigung  folgt:
folgt:

Sprungantwort PT1-System im Zeitbereich
PT1-System Sprungantwort berechnen
Um die Sprungantwort im Zeitbereich zu bestimmen, muss sie aus dem Bildbereich zurück transformiert werden.

Um nicht die aufwändige Laplacerücktransformation durchführen zu müssen, bietet es sich an, an dieser Stelle die Korrespondenztabellen für die Laplacerücktransformation zu nutzen. Da sich für  kein Eintrag finden lässt, wird an hier die Partialbruchzerlegung genutzt, um Ausdrücke zu erhalten die in der Korrespondenztabelle enthalten sind.
kein Eintrag finden lässt, wird an hier die Partialbruchzerlegung genutzt, um Ausdrücke zu erhalten die in der Korrespondenztabelle enthalten sind.
Durch Partialbruchzerlegung ergibt sich:

Für  und
und  ergibt sich aus der Korrespondenztabelle:
ergibt sich aus der Korrespondenztabelle:
 und
und 
Daraus folgt für die Sprungantwort h(t):


Graphische Darstellung der Sprungantwort eines PT1 Systems
In der Graphischen Darstellung von  ist zu erkennen, dass der Endwert der Sprungantwort dem Proportionalitätsfaktor K des PT1-Systems entspricht.
ist zu erkennen, dass der Endwert der Sprungantwort dem Proportionalitätsfaktor K des PT1-Systems entspricht.
An dieser Stelle können die gewonnen Erkenntnisse aus der Endwertbestimmung im Bildbereich mit dem Graphen abgeglichen und die Übereinstimmung festgestellt werden.
Die Zeitkonstante T lässt sich durch den Schnittpunkt der Tangente im Angangspunkt mit K bestimmen. Das bedeutet also je größer T ist, desto langsamer nährt sich die Sprungantwort ihrem Endwert.
Zusammenhang der Impulsfunktion, Sprungfunktion und Rampenfunktion
Die Übersicht zeigt den Zusammenhang zwischen der Impulsfunktion , der Sprungfunktion und der Rampenfunktion. Im Zeitbereich sind die einzelnen Funktionen durch Integrieren bzw. Differenzieren ineinander zu überfuhren.
 und
und 
Im Bildbereich entspricht die Integration einer Multiplikation mit  . Daher ergibt sich folgender Zusammenhang:
. Daher ergibt sich folgender Zusammenhang:
 und
und 
Diese Beziehungen lassen sich auch nutzen, um beispielsweise aus der Impulsantwort auf die Sprungantwort zu schließen. So ergibt sich die Sprungantwort H(s) eines Systems im Bildbereich aus der Multiplikation der Impulsantwort G(s) mit  .
.