PI Regler
In diesem Artikel geben wir dir eine Zusammenfassung zum PI Regler. Dazu behandeln wir die Gleichung des PI Reglers im Zeitbereich, die Übertragungsfunktion sowie die Sprungantwort und das zugehörige Bodediagramm. Schau dir am besten direkt unser Video an, in dem wir dir das Wichtigste in Kürze erklären.
Inhaltsübersicht
Definition des PI Reglers
Der PI Regler setzt sich aus den Anteilen des P- und I- Gliedes zusammen und entspricht damit einem PI Glied.
Aufgrund dieser Vorteile und seinem vergleichsweisen unkomplizierten Aufbau ist der PI Regler, der in der Praxis am häufigsten verwendete Regler.
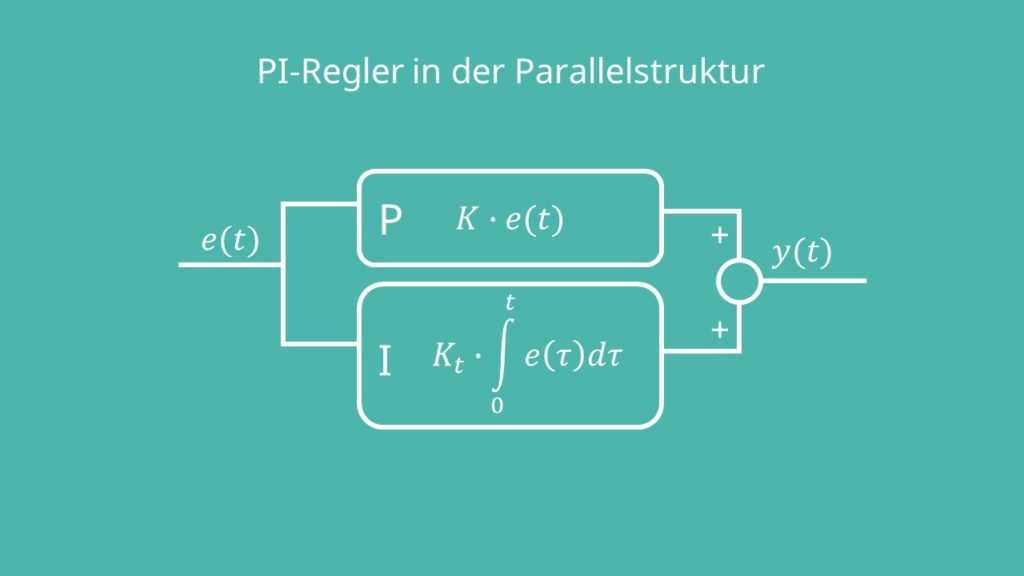
Im Blockschaltbild lässt sich der PI Regler in der Parallelstruktur folgendermaßen darstellen:
Gleichung des PI Reglers im Zeitbereich
Aus dem Blockschaltbild lässt sich die Gleichung für die Stellgröße y(t) abhängig von der Regeldifferenz e(t) ableiten:

Um die Gleichung in der Standartform zu erhalten wird  durch
durch  ersetzt und anschließend
ersetzt und anschließend  ausgeklammert. Für die Reglergleichung ergibt sich damit:
ausgeklammert. Für die Reglergleichung ergibt sich damit:

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Nachstellzeit des PI Reglers
 wird dabei als Nachstellzeit des Reglers bezeichnet. Die Nachstellzeit, bezeichnet die Zeit, die verstreichen muss, damit der I-Anteil gleich dem P-Anteil ist. Gleichzeitig gibt sie ein Maß dafür an wie stark der Einfluss des I-Anteils ist. Ist die Nachstellzeit groß, so ist der Einfluss des I-Anteils gering und umgekehrt.
wird dabei als Nachstellzeit des Reglers bezeichnet. Die Nachstellzeit, bezeichnet die Zeit, die verstreichen muss, damit der I-Anteil gleich dem P-Anteil ist. Gleichzeitig gibt sie ein Maß dafür an wie stark der Einfluss des I-Anteils ist. Ist die Nachstellzeit groß, so ist der Einfluss des I-Anteils gering und umgekehrt.
Herleitung der Übertragungsfunktion aus der Differenzialgleichung
Die Differenzialgleichung des PI Reglers lautet wie bereits oben erwähnt:

Nach der Transformation in den Bildbereich ergibt sich:

Durch Ausklammern von E(s) ergibt sich:


Da die Übertragungsfunktion das Verhältnis von Ein- zu Ausgang beschreibt, wird die Gleichung noch nach  umgeformt.
umgeformt.
Für die Übertragungsfunktion des PI Reglers ergibt sich also:

Sprungantwort des PI Reglers
In Bezug auf die Parallelstruktur des PI Reglers im Blockschaltbild lässt sich die Sprungantwort aus der Summe der Sprungantworten eines P-Reglers und eines I-Reglers bilden.
Aus der Sprungantwort können die Reglerparameter  und
und  ermittelt werden.
ermittelt werden.
Berechnung der Sprungantwort des PI Reglers
Die Sprungantwort H(s) des PI Reglers im Bildbereich ergibt sich aus dem Produkt des Einheitssprungs und der Übertragungsfunktion des Reglers:


Durch Umformung in den Zeitbereich durch zur Hilfenahme einer Korrespondenztabelle ergibt sich:
Dies entspricht einer Geraden mit der Steigung  welche die y-Achse in
welche die y-Achse in  schneidet und stimmt damit mit der oberen Abbildung überein (negative Zeiten t werden nicht betrachtet).
schneidet und stimmt damit mit der oberen Abbildung überein (negative Zeiten t werden nicht betrachtet).
Bodediagramm des PI Reglers
Aus dem Bodediagramm
des PI Reglers geht hervor, dass er sich für Signale niedriger Frequenz  ähnlich wie ein I-Regler verhält, für Signale höherer Frequenz
ähnlich wie ein I-Regler verhält, für Signale höherer Frequenz  verhält er sich wie ein P-Regler.
verhält er sich wie ein P-Regler.

Außerdem ist zu erkennen, dass ein PI-Regler dazu dienen kann die Phase einer Regelstrecke von 0° bis -90°abzusenken, um beispielsweise einen gewünschten Phasenrand zu erhalten. Für Signale der Frequenz beträgt die Phasendifferenz genau -45°. Ab diesem Punkt fällt bzw. steigt die Phase mit 45° pro Dekade bis -90° bzw. 0°.
Aus dem Bodediagramm ist es also möglich die Kennwerte  und
und  abzulesen und daraus auf die Übertragungsfunktion des PI Reglers zu schließen.
abzulesen und daraus auf die Übertragungsfunktion des PI Reglers zu schließen.
Überblick über die Eigenschaften des PI Reglers
Aufgrund seines I-Anteils weist der PI-Regler keine bleibende Regelabweichung auf, der Soll- und der Istwert der Regelgröße stimmen also nach einiger Zeit überein.
Der P-Anteil führt außerdem dazu, dass der PI- Regler im Vergleich zu einem I-Regler schneller auf Änderungen der Führungsgröße reagiert.
Allgemein eignet sich das PI Glied vor allem für das Regeln von Regelstrecken geringerer Ordnung (1. und 2. Ordnung) und kommt aufgrund seines relativ unkomplizierten Aufbaus (nur zwei Einstellparameter  und T) in der Praxis häufig zum Einsatz.
und T) in der Praxis häufig zum Einsatz.