Henderson Hasselbalch Gleichung
In diesem Artikel stellen wir dir die Henderson Hasselbalch Gleichung vor. Wir beschreiben ihr Anwendungsgebiet näher und zeigen mit konkreten Beispielen, wie du sie zur Berechnung des pH-Werts nutzen kannst.
Wenn du eher der audio-visuellen Lerntyp bist, eignet sich unser Lernvideo hervorragend dazu, dir dieses Thema näher zu bringen.
Inhaltsübersicht
Henderson Hasselbalch Gleichung einfach erklärt
Mit der Henderson Hasselbalch Gleichung wird der Zusammenhang zwischen dem pH-Wert und der Lage des Gleichgewichts einer Säure-Base-Reaktion beschrieben.
 ), sogenannten Pufferlösungen, angewendet wird.
), sogenannten Pufferlösungen, angewendet wird.Sie wird häufig auch als Henderson Hasselbach Gleichung bezeichnet. Dies ist allerdings falsch, da ihr Name auf die zwei Chemiker Lawrence J. Henderson und Karl Albert Hasselbalch zurückgeht. Die Schreibweise Henderson-Hasselbalch-Gleichung ist in der Fachliteratur am häufigsten vertreten.
Die Henderson Hasselbalch Gleichung lautet:
 oder auch
oder auch 
Der pH-Wert ist gleich dem  -Wert + dem Zehnerlogarithmus des Konzentrationsverhältnisses von Salz zu Säure. Die alternative Form der Gleichung erhälst du durch die Anwendung der Rechenregeln des Logarithmus eines Quotienten.
-Wert + dem Zehnerlogarithmus des Konzentrationsverhältnisses von Salz zu Säure. Die alternative Form der Gleichung erhälst du durch die Anwendung der Rechenregeln des Logarithmus eines Quotienten.
Henderson Hasselbalch Gleichung Herleitung
Das Aufstellen der Gleichung ist in zwei Schritte untergliedert: Zuerst stellen wir anhand einer allgemeinen Säure-Base-Gleichung unter Anwendung des Massenwirkungsgesetzes eine Funktion für unsere Gleichgewichtskonstante auf.
Im zweiten Schritt führen wir einige Rechenoperationen durch, um von der Gleichgewichtskonstante auf die Säurekonstante und zuletzt auf den pH-Wert zu schließen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Allgemeine Säure-Base-Reaktionsgleichung
Um die Henderson Hasselbalch Gleichung herzuleiten, benötigen wir zunächst einmal die allgemeine Säure-Base-Reaktionsgleichung:

Dabei ist  eine allgemeine schwache Säure und
eine allgemeine schwache Säure und  das dazugehörige Anion.
das dazugehörige Anion.
Diese Reaktionsgleichung kann als nachfolgende Form des Massenwirkungsgesetzes formuliert werden:
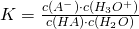
Umformung des Massenwirkungsgesetzes
Nun multiplizieren wir die Gleichung mit  und ersetzen die Gleichgewichtskonstante
und ersetzen die Gleichgewichtskonstante  durch die Säurekonstante
durch die Säurekonstante  . Wobei folgende Beziehung zwischen den beiden Größen gilt:
. Wobei folgende Beziehung zwischen den beiden Größen gilt:

Aus unserem Massenwirkungsgesetz ergibt sich dadurch:
 ; oder auch;
; oder auch; 
Anschließend logarithmieren wir die Gleichung zur Basis 10, wobei wir die Rechenregel für den Logarithmus von Produkten beachten werden müssen:

Daraus folgt für unsere Gleichung:

Nun führen wir noch die Rechenoperationen  und
und  durch, womit sich folgende Gleichung ergibt:
durch, womit sich folgende Gleichung ergibt:

Folgende Definitionen für den pH-Wert und den  -Wert kennen wir schon:
-Wert kennen wir schon:
pH  und p
und p
Setzen wir diese Definitionen in unsere Formel ein, so ergibt sich die Henderson Hasselbalch Gleichung:

Diese Gleichung kann noch umformuliert werden, indem wir uns die Rechenregel für den Logarithmus von Quotienten zunutze machen, welche allgemein lautet:

Damit erhalten wir die alternative Form der Henderson Hasselbalch Gleichung:

Aus den Gleichungen erkennen wir, dass der pH-Wert weitestgehend unabhängig von der Gesamtkonzentration einer Pufferlösung ist. Viel einflussreicher ist hier das Verhältnis der Konzentrationen von Salz zu Säure.
Henderson Hasselbalch Gleichung bei Puffern
Als Pufferlösungen bezeichnet man im allgemeinen wässrige Lösungen, deren pH-Wert durch Zugabe einer Säure oder einer Base nur geringfügig verändert wird. In derartigen Lösungen befindet sich ein konjugiertes Säure-Base-Paar, wodurch die Säure  -Ionen und die Base
-Ionen und die Base  -Ionen neutralisieren kann. Pufferlösungen können hergestellt werden, indem schwache Säuren oder Basen mit ihren jeweiligen Salzen vermischt werden.
-Ionen neutralisieren kann. Pufferlösungen können hergestellt werden, indem schwache Säuren oder Basen mit ihren jeweiligen Salzen vermischt werden.
Mithilfe dieser Pufferwirkung können starke pH-Wert Änderungen abgedämpft werden. Diese Funktion ist etwa für die Gesundheit des Menschen äußerst wichtig, da sich bereits geringe Abweichungen des pH-Werts im Körper lebensgefährlich auswirken können. Aus diesem Grund enthält das Blut mehrere Puffersysteme, um stoffwechselbedingte pH-Wert Änderungen abzupuffern.
Im Pufferbereich der Lösung entspricht das Konzentrationsverhältnis von Salz zu Säure, also  , dem Verhältnis
, dem Verhältnis  . Hierbei handelt es sich bei
. Hierbei handelt es sich bei  um den Titrationsgrad, also dem Verhältnis der Stoffmenge einer Maßlösung zur Stoffmenge einer Probelösung. Die Henderson Hasselbalch Gleichung lässt sich demnach auch schreiben als:
um den Titrationsgrad, also dem Verhältnis der Stoffmenge einer Maßlösung zur Stoffmenge einer Probelösung. Die Henderson Hasselbalch Gleichung lässt sich demnach auch schreiben als:

Zu beachten ist hier, dass die Henderson Hasselbalch Gleichung im Bereich von  und
und  oder bei noch stärkerer Verdünnung (
oder bei noch stärkerer Verdünnung ( ) nur noch eingeschränkt angewendet werden kann. In diesen Fällen müssten zusätzlich die Protolyse des Salzes bzw. der Säure mit dem Lösungsmittel oder die Autoprotolyse des Wassers um pH
) nur noch eingeschränkt angewendet werden kann. In diesen Fällen müssten zusätzlich die Protolyse des Salzes bzw. der Säure mit dem Lösungsmittel oder die Autoprotolyse des Wassers um pH  für die Konzentrationsberechnung berücksichtigt werden.
für die Konzentrationsberechnung berücksichtigt werden.
Um den pH-Wert derartiger Lösungen korrekt zu berechnen, müssten die benötigten Gleichungen aus dem Massenwirkungsgesetz hergeleitet, und, anstelle der Konzentrationen, die Aktivitäten genutzt werden.
Henderson Hasselbalch Gleichung Beispiel
Damit wir die Anwendung der Henderson Hasselbalch Gleichung besser verstehen können, schauen wir uns ein konkretes Beispiele an. Weshalb wir diese nun nur bei Pufferlösungen anwenden können, verdeutlichen wir mit nochmals mit diesem Beispiel.
Gegeben sind zwei unterschiedlich konzentrierte Ammonium-/ Ammoniakpuffer, die jeweils mit der gleichen Menge an Salzsäure versetzt werden.
Für unsere erste Pufferlösung sind folgende Angaben gegeben:
 ;
;  ;
;  ; pH
; pH 
Im Vergleich zur ersten Lösung ist unsere zweite zehnfach verdünnt und ebenfalls äquimolar, also die Konzentration der Säure und der konjugierten Base sind gleich hoch. Folgende Werte sind bekannt:
 ;
;  ;
;  ; pH
; pH 
Nachfolgende Angaben sind für unsere Salzsäure gegeben:
 ;
; 
Die zu unseren Lösungen hinzugefügte Stoffmenge an  –Ionen berechnet sich mit der nächsten Formel:
–Ionen berechnet sich mit der nächsten Formel:



Nun sollen wir die pH-Werte beider Lösungen nach Zugabe der Salzsäure berechnen.
Da unsere Pufferlösungen äquimolar sind gilt:
pH 
Für unsere erste Pufferlösung ergeben sich folgende Konzentrationen durch die Säurezugabe:
 ;
; 
Nun berechnen wir den pH-Wert mit diesen Angaben mit der Henderson Hasselbalch Gleichung:
pH 
Wir sehen, dass sich der pH-Wert nur geringfügig vom Anfangswert unterscheidet. Die Pufferlösung konnte den Säurestoß abfangen.
Unter den gleichen Rahmenbedingungen ergeben sich nachfolgende Werte für unsere stärker verdünnte Lösung:
 ;
; 
Wir erkennen, dass durch die Säurezugabe, das gesamte Ammoniak in der Lösung in die konjugierte Säure Ammonium überführt wurde. Aus diesem Grund können wir die Henderson Hasselbalch Gleichung nicht hernehmen, sondern müssen mit der Formel zur Berechnung des pH-Werts schwacher Säuren fortfahren. Daraus folgt:
pH 


Hier sehen wir, dass sich der pH-Wert stark verringert hat, die Säurezugabe konnte nicht abgepuffert werden.
