Mischungskreuz
Wie du mit dem Mischungskreuz in der Chemie ganz einfach Mischungen mit einem gewünschten Mengenverhältnis herstellen kannst und wie du dieses Schema kinderleicht selbst aufstellst, zeigen wir dir hier.
Du willst den Inhalt dieses Artikels noch schneller verstehen? Dann schau dir unser Video zum Mischungskreuz an.
Inhaltsübersicht
Das Mischungskreuz einfach erklärt
Das Mischungskreuz – auch Andreaskreuz genannt – ist eine einfache schematische Methode, die in der Chemie häufig beim Mischen von Lösungen eingesetzt wird. Mit dem Mischungskreuz kann man berechnen, welche Massen von zwei gegebenen Ausgangslösungen miteinander gemischt werden müssen, um eine Lösung mit einem bestimmten Massenanteil eines gelösten Stoffes herzustellen. Der vorgegebene Massenanteil in der Ziellösung liegt dabei zwischen den Massenanteilen in den beiden Ausgangslösungen. Diese Ausgangslösungen bezeichnet man in der Chemie auch als Stammlösungen.
Das Mischungskreuz funktioniert allerdings nicht nur für Lösungen. Auch für andere Mischungen zum Beispiel Legierungen kann es näherungsweise eingesetzt werden. Es hat auch Anwendungen außerhalb der Chemie – zum Beispiel in der Ökonomie.
Das Mischungskreuz eignet sich zur Berechnung eines Mischungsverhältnisses, das benötigt wird, um eine Lösung mit einem vorgegebenen Massenanteil zu erhalten. Es beruht auf dem Massenerhaltungssatz und eignet sich daher nur bedingt für Berechnungen mit Volumina.
Mischungskreuz schematische Berechnung
Links im Mischungskreuz werden die Massenanteile der Ausgangslösungen übereinander aufgeschrieben. Oben trägt man den Massenanteil der höher konzentrierten Lösung ein. In der Mitte des Mischungskreuzes wird der Massenanteil der Ziellösung eingetragen.
Nun werden von den Massenanteilen der Ausgangslösungen jeweils der Massenanteil der Ziellösung subtrahiert und die Ergebnisse diagonal auf der rechten Seite eingetragen.
Als Ergebnis erhält man, dass die rechts oben die benötigten Massenanteile der höher konzentrieren Lösung und rechts unten die benötigten Massenteile der weniger konzentrierten Lösung stehen. Die negativen Vorzeichen bei den Ergebnissen können ignoriert werden, denn man rechnet nur mit den Beträgen. Die Gesamtzahl der Massenanteile ergibt sich als Summe der rechten Seite.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Berechnung bei bekannten Massenanteilen
Angenommen, du hast zwei Ausgangslösungen 1 und 2 mit den Massen  und
und  . Nun vermischst du diese Ausgangslösungen in einem bestimmten Verhältnis und erhälst die Ziellösung mit der Masse
. Nun vermischst du diese Ausgangslösungen in einem bestimmten Verhältnis und erhälst die Ziellösung mit der Masse  . Das benötigte Verhältnis der Ausgangslösungen erhälst du aus dem Mischungskreuz.
. Das benötigte Verhältnis der Ausgangslösungen erhälst du aus dem Mischungskreuz.
Das Prinzip des Mischungskreuzes basiert auf den Massenerhaltungssatz: Beim Mischen der Lösungen ändern sich weder die Massen der Lösungen selbst noch die Massen des in ihnen gelösten Stoffes A.
Die Masse des gelösten Stoffes A in der Ziellösung  setzt sich zusammen aus den Massen des gelösten Stoffes in den beiden ungemischten Ausgangslösungen
setzt sich zusammen aus den Massen des gelösten Stoffes in den beiden ungemischten Ausgangslösungen  und
und  .
.

Außerdem setzt sich die Masse der Ziellösung  aus den Massen der Ausgangslösung 1
aus den Massen der Ausgangslösung 1  und der Ausgangslösung 2
und der Ausgangslösung 2  zusammen.
zusammen.

In der ersten Gleichung können die Massen des gelösten Stoffes A  mithilfe ihrer zugehörigen Massenanteile
mithilfe ihrer zugehörigen Massenanteile  in der Lösung dargestellt werden. Dazu wird
in der Lösung dargestellt werden. Dazu wird

eingesetzt und man erhält dabei man die Gleichung:

Setzt man hierin die zweite Gleichung ein und löst nach dem Verhältnis der beiden Massen der Ausgangslösungen  auf, erhält man
auf, erhält man

Weil die Gleichung auf dem Massenerhaltungssatz basiert, können mit ihr nur Berechnungen gemacht werden, bei denen Angaben in Massenanteilen gegeben sind. In der Chemie ist das zum Beispiel der Fall, wenn von einer x-prozentigen Säure oder Base gesprochen wird.
Die Berechnungen wie diese kann man ganz einfach mit dem Schema des Mischungskreuzes machen.
Berechnungen bei gegebenen Volumina
Berechnungen mit Volumina und Konzentrationen (zum Beispiel mit Angaben in mol/l oder g/l) sind nur möglich, wenn man die Dichten kennt und in Massenanteile umrechnen kann. Der Grund dafür ist, dass sich das Gesamtvolumen beim Mischen oftmals ändert. Mischt man zum Beispiel 500 ml Wasser und 500 ml Ethanol ergibt in der Realität nicht ein Volumen von 1000 ml. Man spricht von einer Volumenkontraktion.
Wenn man diese Volumenänderung außer Acht lässt, kann man eine ähnliche Gleichung wie die oben gezeigte aufstellen:

Verwendete Formelzeichen
-
 Volumen der entsprechenden Lösung x
Volumen der entsprechenden Lösung x -
 Konzentration des gelösten Stoffes A in der entsprechenden Lösung x
Konzentration des gelösten Stoffes A in der entsprechenden Lösung x
Mischungskreuz Beispiele
Hier möchten wir dir einige Beispiele zeigen, bei denen das Mischungskreuz eingesetzt werden kann.
Mischen von Flüssigkeiten
Betrachten wir im folgenden ein Beispiel aus dem Alltag, nämlich das Mischen einer Saftschorle und die Berechnung der Mengen und das Mischungsverhältnis von Saft und Wasser. Des Weiteren betrachten wir ein direktes Beispiel aus der Chemie, wenn wir eine Säureverdünnung berechnen.
Saftschorle
Apfelsaft enthält ungefähr genauso viel Zucker wie ein Glas Cola. Das sind ungefähr zwölf Gramm Zucker pro 100 ml. Wenn du annimmst, dass ein Liter Apfelsaft genau einen Kilo wiegt, dann entsprechen die darin enthaltenen zwölf Gramm einem Massenanteil von 12%. Damit der Apfelsaft nicht ganz so intensiv süß schmeckt, kann man ihn etwas mit Wasser verdünnen. Nehmen wir an, du möchtest 5% Zucker in deiner Apfelschorle haben. Das Mischungskreuz sieht dann so aus.
Auf der linken Seite des Mischungskreuzes trägst du oben für den Anteil an Zucker im Apfelsaft die Zahl 12 und unten die Zahl 0 für den Anteil an Zucker im Wasser ein. In der Mitte schreibst du mit der Zahl 5 den gewünschten Zuckeranteil in der Apfelschorle. Jetzt kannst du die rechte Seite berechnen: Du brauchst | 0 – 5 | = 5 Teile Apfelsaft und | 12 – 5 | = 7 Teile Wasser. Rechts oben steht also eine 5 und rechts unten eine 7.
Deine Zielmischung besteht folglich aus 5 + 7 = 12 Teilen. Für ein Glas mit einem Volumen von 200 ml brauchst du also 5/12 · 200 ml = 83 ml Apfelsaft und 7/12 · 200 ml = 117 ml Wasser zur Verdünnung.
Säureverdünnung
Im Chemielabor steht eine konzentrierte 37%ige und eine verdünnte 2%ige Salzsäure bereit. Daraus sollen 500 g einer 10%igen Lösung hergestellt werden.
Links stehen also oben die Zahl 37 und darunter die Zahl 2. In der Mitte des Schemas befindet sich die Zahl 10. Zur Herstellung der Mischung werden | 2 – 10 | = 8 Teile der 37%igen und |37 – 10 | = 27 Teile der 2%igen Lösung benötigt. Diese Zahlen stehen auf der rechten Seite des Schemas. Für 500 g der Ziellösung sind dafür also 8/35 · 500 g = 114 g der konzentrierten und 27/35 · 500 g = 386 g der verdünnten Salzsäure notwendig.
Mischungskreuz in der Ökonomie
Mit dem Mischungskreuz können auch wirtschaftliche Berechnungen getätigt werden. Hier ist ein Beispiel aus dem kaufmännischen Bereich:
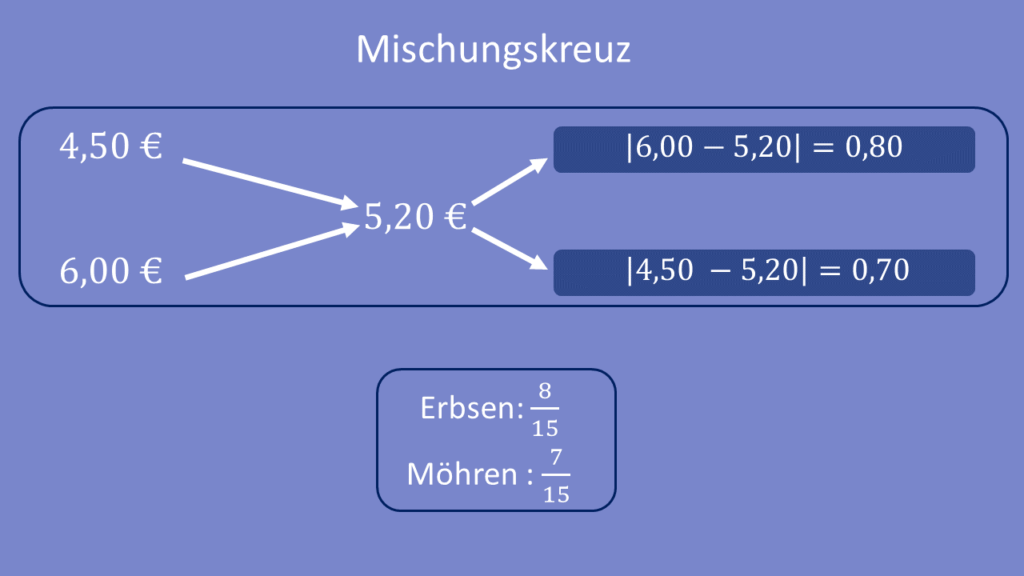
Ein Konservenhersteller bietet Erbsen zu einem Preis von 4,50 Euro pro Kilo und Möhren zu einem Preis von 6,00 Euro pro Kilo an. Er möchte sein Angebot erweitern und beide Gemüsesorten auch als Mischung zu einem Preis von 5,20 Euro pro Kilo verkaufen.
Stellt man das Mischungskreuz auf, ergeben sich Werte von 0,80 und 0,70 auf der rechten Seite. Erbsen und Möhren müssen also im Verhältnis von 0,80 zu 0,70 bzw. 8 zu 7 gemischt werden – d.h. in der Mischung sind mehr Erbsen als Möhren enthalten.
Mischungskreuz für Legierungen
Mithilfe des Mischungskreuzes kann auch die Zusammensetzung von Metalllegierungen abgeschätzt werden. Dazu müssen die Dichten der reinen Metalle und die Dichte der Legierung bekannt sein. Die berechneten Werte sind dabei nur Näherungen, weil Änderungen in der Kristallstruktur auftreten.
Eine Legierung aus Gold und Silber hat eine Dichte von 18,55 g/cm³. Reines Gold besitzt eine Dichte von 19,30 g/cm³ und reines Silber eine Dichte von 10,49 g/cm³.
Mit dem Mischungskreuz ergeben sich Werte von 7,76 und 0,75 auf der rechten Seite. Das bedeutet, dass näherungsweise 7,76/(7,76+0,75) = 0,91 also 91 Massen-% Gold und 0,75/(7,76+0,75) = 0,09 = 9 Massen-% Silber in der Legierung vorliegen. Der tatsächliche Wert liegt dagegen bei ca. 95 Massen-% Gold.

 Masse der entsprechenden Lösung x
Masse der entsprechenden Lösung x Masse des gelösten Stoffes A in der entsprechenden Lösung x
Masse des gelösten Stoffes A in der entsprechenden Lösung x Massenanteil des gelösten Stoffes A in entsprechenden Lösung x
Massenanteil des gelösten Stoffes A in entsprechenden Lösung x