Dichtefunktion Übung
Was ist eine Dichtefunktion? Hier klären wir diese Frage und zeigen dir wie man konkrete Aufgaben lösen kann anhand einfacher Beispiele.
Du lässt dir alles zur Dichtefunktionen lieber kurz und knackig erklären ohne Lesen? Unsere Videos Dichtefunktion und Dichtefunktion Übung können das besser als jeder Professor oder Lehrer!
Inhaltsübersicht
Dichtefunktion berechnen
Wir wollen die Frage beantworten, mit welcher Wahrscheinlichkeit ein 100m Läufer diese Strecke in unter 12 Sekunden bewältigt (Beispiel 1). Anschließend wollen wir es noch genauer wissen und stellen uns die Frage: Wie wahrscheinlich ist es, dass er die 100m in 11 – 12 Sekunden zurücklegt (Beispiel 2)?
Dichtefunktion Formel
Gehen wir von einer Normalverteilung aus, so ist die Formel der Dichtefunktion folgende:

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Erwartungswert Dichtefunktion
Betrachtet man die beispielsweise die zentralen Maßzahlen der Statistik wie den Erwartungswert , die Varianz oder die Standardabweichung , kann man bereits Aussagen über die Wahrscheinlichkeitsverteilung treffen.
In unserem Fall sind der Erwartungswert und die Varianz gegeben mit  und
und  .
.
Da man sich unter den bloßen Zahlenwerten nur schwer etwas vorstellen kann, hilft es diese graphisch darzustellen.
Dichtefunktion zeichnen
Die Dichtefunktion ist eine visuelle Darstellung der Verteilung deiner Variablen. Sie zeigt also an, in welchem Bereich die Zufallsvariable am stärksten ausgeprägt ist. Zeichnen wir die Dichtefunktion für den 100 Meter Läufer, könnte das zum Beispiel so aussehen:
Man kann ablesen, dass es am wahrscheinlichsten ist, dass ein Läufer die Strecke in rund 14 Sekunden bewältigt. Der Graph verrät uns außerdem, dass es ziemlich unwahrscheinlich ist, dass jemand die Strecke in unter 10 beziehungsweise über 17 Sekunden läuft.
Dichtefunktion Wahrscheinlichkeit berechnen
Wie vorhin bereits erklärt, muss man die Dichtefunktion integrieren, um die Verteilungsfunktion zu erhalten. Nur mit dieser kann man im stetigen Fall die Wahrscheinlichkeit berechnen.
Wir wissen, dass unsere Werte normalverteilt sind, somit rechnen wir mit der Verteilungsfunktion der Normalverteilung. Um die Wahrscheinlichkeit aus der Verteilungstabelle ablesen zu können, müssen wir die Verteilungsfunktion auf die der Standardnormalverteilung transformieren. Dazu setzten wir einfach unsere gegebenen Werte ein uns schlagen den errechneten Wert für in der Verteilungstabelle nach.
Beispiel 1
Kommen wir auf unsere Fragestellung von vorhin zurück: Mit welcher Wahrscheinlichkeit ist der Läufer schneller als 12 Sekunden?
Mathematisch ausgedrückt bedeutet das:

Die Wahrscheinlichkeit für  entspricht dem Funktionswert der Verteilungsfunktion an der Stelle x gleich zwölf.
entspricht dem Funktionswert der Verteilungsfunktion an der Stelle x gleich zwölf.


Unser gesuchter Wert ist 12 und der Erwartungswert ist gegeben mit 14. Da wir nur die Varianz mit 4 gegeben haben, müssen wir noch die Wurzel aus dieser ziehen, um die Standardabweichung zu erhalten.


Lesen wir diesen Wert aus der Verteilungstabelle der standardisierten Normalverteilung ab, so erhalten wir eine Wahrscheinlichkeit von 
| z/Φ(z) | 0 | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,09 |
| 0 | 0,5 | 0,50399 | 0,50798 | 0,51197 | 0,51595 | 0,51994 | 0,52392 | 0,5279 | 0,53188 | 0,53586 |
| 0,1 | 0,53983 | 0,5438 | 0,54776 | 0,55172 | 0,55567 | 0,55962 | 0,56356 | 0,56749 | 0,57142 | 0,57535 |
| 0,2 | 0,57926 | 0,58317 | 0,58706 | 0,59095 | 0,59483 | 0,59871 | 0,60257 | 0,60642 | 06,1026 | 0,61409 |
| 0,3 | 0,61791 | 0,62172 | 0,62552 | 0,6293 | 0,63307 | 0,63683 | 0,64058 | 0,64431 | 0,64803 | 0,65173 |
| 0,4 | 0,65542 | 0,6591 | 0,66276 | 0,6664 | 0,67003 | 0,67364 | 0,67724 | 0,68082 | 0,68439 | 0,68793 |
| 0,5 | 0,69146 | 0,69497 | 0,69847 | 0,70194 | 0,7054 | 0,70884 | 0,71226 | 0,71566 | 0,71904 | 0,7224 |
| 0,6 | 0,72575 | 0,72907 | 0,73237 | 0,73565 | 0,73891 | 0,74215 | 0,74537 | 0,74857 | 0,75175 | 0,7549 |
| 0,7 | 0,75804 | 0,76115 | 0,76424 | 0,7673 | 0,77035 | 0,77337 | 0,77637 | 0,77935 | 0,7823 | 0,78524 |
| 0,8 | 0,78814 | 0,79103 | 0,79389 | 0,79673 | 0,79955 | 0,80234 | 0,80511 | 0,80785 | 0,81057 | 0,81327 |
| 0,9 | 0,81594 | 0,81859 | 0,82121 | 0,82381 | 0,82639 | 0,82894 | 0,83147 | 0,83398 | 0,83646 | 0,83891 |
| 1 | 0,84134 | 0,84375 | 0,84614 | 0,84849 | 0,85083 | 0,85314 | 0,85543 | 0,85769 | 0,85993 | 0,86214 |
| 1,1 | 0,86433 | 0,8665 | 0,86864 | 0,87076 | 0,87286 | 0,87493 | 0,87698 | 0,879 | 0,881 | 0,88298 |
| 1,2 | 0,88493 | 0,88686 | 0,88877 | 0,89065 | 0,89251 | 0,89435 | 0,89617 | 0,89796 | 0,89973 | 0,90147 |
| 1,3 | 0,9032 | 0,9049 | 0,90658 | 0,90824 | 0,90988 | 0,91149 | 0,91309 | 0,91466 | 0,91621 | 0,91774 |
| 1,4 | 0,91924 | 0,92073 | 0,9222 | 0,92364 | 0,92507 | 0,92647 | 0,92785 | 0,92922 | 0,93056 | 0,93189 |
| 1,5 | 0,93319 | 0,93448 | 0,93574 | 0,93699 | 0,93822 | 0,93943 | 0,94062 | 0,94179 | 0,94295 | 0,94408 |
| 1,6 | 0,9452 | 0,9463 | 0,94738 | 0,94845 | 0,9495 | 0,95053 | 0,95154 | 0,95254 | 0,95352 | 0,95449 |
| 1,7 | 0,95543 | 0,95637 | 0,95728 | 0,95818 | 0,95907 | 0,95994 | 0,9608 | 0,96164 | 0,96246 | 0,96327 |
| 1,8 | 0,96407 | 0,96485 | 0,96562 | 0,96638 | 0,96712 | 0,96784 | 0,96856 | 0,96926 | 0,96995 | 0,97062 |
| 1,9 | 0,97128 | 0,97193 | 0,97257 | 0,9732 | 0,97381 | 0,97441 | 0,975 | 0,97558 | 0,97615 | 0,9767 |
| 2 | 0,97725 | 0,97778 | 0,97831 | 0,97882 | 0,97932 | 0,97982 | 0,9803 | 0,98077 | 0,98124 | 0,98169 |
| 2,1 | 0,98214 | 0,98257 | 0,983 | 0,98341 | 0,98382 | 0,98422 | 0,98461 | 0,985 | 0,98537 | 0,98574 |
| 2,2 | 0,9861 | 0,98645 | 0,98679 | 0,98713 | 0,98745 | 0,98778 | 0,98809 | 0,9884 | 0,9887 | 0,98899 |
| 2,3 | 0,98928 | 0,98956 | 0,98983 | 0,9901 | 0,99036 | 0,99061 | 0,99086 | 0,99111 | 0,99134 | 0,99158 |
| 2,4 | 0,9918 | 0,99202 | 0,99224 | 0,99245 | 0,99266 | 0,99286 | 0,99305 | 0,99324 | 0,99343 | 0,99361 |
| 2,5 | 0,99379 | 0,99396 | 0,99413 | 0,9943 | 0,99446 | 0,99461 | 0,99477 | 0,99492 | 0,99506 | 0,9952 |
| 2,6 | 0,99534 | 0,99547 | 0,9956 | 0,99573 | 0,99585 | 0,99598 | 0,99609 | 0,99621 | 0,99632 | 0,99643 |
| 2,7 | 0,99653 | 0,99664 | 0,99674 | 0,99683 | 0,99693 | 0,99702 | 0,99711 | 0,9972 | 0,99728 | 0,99736 |
| 2,8 | 0,99744 | 0,99752 | 0,9976 | 0,99767 | 0,99774 | 0,99781 | 0,99788 | 0,99795 | 0,99801 | 0,99807 |
| 2,9 | 0,99813 | 0,99819 | 0,99825 | 0,99831 | 0,99836 | 0,99841 | 0,99846 | 0,99851 | 0,99856 | 0,99861 |
| 3 | 0,99865 | 0,99869 | 0,99874 | 0,99878 | 0,99882 | 0,99886 | 0,99889 | 0,99893 | 0,99896 | 0,999 |
| 3,1 | 0,99903 | 0,99906 | 0,9991 | 0,99913 | 0,99916 | 0,99918 | 0,99921 | 0,99924 | 0,99926 | 0,99929 |
| 3,2 | 0,99931 | 0,99934 | 0,99936 | 0,99938 | 0,9994 | 0,99942 | 0,99944 | 0,99946 | 0,99948 | 0,9995 |
| 3,3 | 0,99952 | 0,99953 | 0,99955 | 0,99957 | 0,99958 | 0,9996 | 0,99961 | 0,99962 | 0,99964 | 0,99965 |
| 3,4 | 0,99966 | 0,99968 | 0,99969 | 0,9997 | 0,99971 | 0,99972 | 0,99973 | 0,99974 | 0,99975 | 0,99976 |
| 3,5 | 0,99977 | 0,99978 | 0,99978 | 0,99979 | 0,9998 | 0,99981 | 0,99981 | 0,99982 | 0,99983 | 0,99983 |
| 3,6 | 0,99984 | 0,99985 | 0,99985 | 0,99986 | 0,99986 | 0,99987 | 0,99987 | 0,99988 | 0,99988 | 0,99989 |
| 3,7 | 0,99989 | 0,9999 | 0,9999 | 0,9999 | 0,99991 | 0,99991 | 0,99992 | 0,99992 | 0,99992 | 0,99992 |
| 3,8 | 0,99993 | 0,99993 | 0,99993 | 0,99994 | 0,99994 | 0,99994 | 0,99994 | 0,99995 | 0,99995 | 0,99995 |
| 3,9 | 0,99995 | 0,99995 | 0,99996 | 0,99996 | 0,99996 | 0,99996 | 0,99996 | 0,99996 | 0,99997 | 0,99997 |
| 4 | 0,99997 | 0,99997 | 0,99997 | 0,99997 | 0,99997 | 0,99997 | 0,99998 | 0,99998 | 0,99998 | 0,99998 |
Somit ist der Läufer mit einer Wahrscheinlichkeit von rund 16% schneller als 12 Sekunden.
Beispiel 2
Soweit ist das ja alles sehr einfach, oder? Aber wie berechnet man nun die Wahrscheinlichkeit, dass der Läufer zum Beispiel zwischen 11 und 12 Sekunden braucht?

Auch das ist keine Hexerei. Du ziehst einfach den Funktionswert der Verteilungsfunktion an der Stelle x gleich elf von dem Funktionswert an der Stelle x gleich zwölf ab.
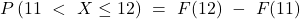
Das wird besonders deutlich, wenn du dir das Ganze graphisch unter der Dichtefunktion vorstellst.
Setzten wir unsere Werte ein, so erhalten wir:





Lesen wir nun die Werte aus der Tabelle der Standardnormalverteilung ab:
| z/Φ(z) | 0 | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,09 |
| 0 | 0,5 | 0,50399 | 0,50798 | 0,51197 | 0,51595 | 0,51994 | 0,52392 | 0,5279 | 0,53188 | 0,53586 |
| 0,1 | 0,53983 | 0,5438 | 0,54776 | 0,55172 | 0,55567 | 0,55962 | 0,56356 | 0,56749 | 0,57142 | 0,57535 |
| 0,2 | 0,57926 | 0,58317 | 0,58706 | 0,59095 | 0,59483 | 0,59871 | 0,60257 | 0,60642 | 06,1026 | 0,61409 |
| 0,3 | 0,61791 | 0,62172 | 0,62552 | 0,6293 | 0,63307 | 0,63683 | 0,64058 | 0,64431 | 0,64803 | 0,65173 |
| 0,4 | 0,65542 | 0,6591 | 0,66276 | 0,6664 | 0,67003 | 0,67364 | 0,67724 | 0,68082 | 0,68439 | 0,68793 |
| 0,5 | 0,69146 | 0,69497 | 0,69847 | 0,70194 | 0,7054 | 0,70884 | 0,71226 | 0,71566 | 0,71904 | 0,7224 |
| 0,6 | 0,72575 | 0,72907 | 0,73237 | 0,73565 | 0,73891 | 0,74215 | 0,74537 | 0,74857 | 0,75175 | 0,7549 |
| 0,7 | 0,75804 | 0,76115 | 0,76424 | 0,7673 | 0,77035 | 0,77337 | 0,77637 | 0,77935 | 0,7823 | 0,78524 |
| 0,8 | 0,78814 | 0,79103 | 0,79389 | 0,79673 | 0,79955 | 0,80234 | 0,80511 | 0,80785 | 0,81057 | 0,81327 |
| 0,9 | 0,81594 | 0,81859 | 0,82121 | 0,82381 | 0,82639 | 0,82894 | 0,83147 | 0,83398 | 0,83646 | 0,83891 |
| 1 | 0,84134 | 0,84375 | 0,84614 | 0,84849 | 0,85083 | 0,85314 | 0,85543 | 0,85769 | 0,85993 | 0,86214 |
| 1,1 | 0,86433 | 0,8665 | 0,86864 | 0,87076 | 0,87286 | 0,87493 | 0,87698 | 0,879 | 0,881 | 0,88298 |
| 1,2 | 0,88493 | 0,88686 | 0,88877 | 0,89065 | 0,89251 | 0,89435 | 0,89617 | 0,89796 | 0,89973 | 0,90147 |
| 1,3 | 0,9032 | 0,9049 | 0,90658 | 0,90824 | 0,90988 | 0,91149 | 0,91309 | 0,91466 | 0,91621 | 0,91774 |
| 1,4 | 0,91924 | 0,92073 | 0,9222 | 0,92364 | 0,92507 | 0,92647 | 0,92785 | 0,92922 | 0,93056 | 0,93189 |
| 1,5 | 0,93319 | 0,93448 | 0,93574 | 0,93699 | 0,93822 | 0,93943 | 0,94062 | 0,94179 | 0,94295 | 0,94408 |
| 1,6 | 0,9452 | 0,9463 | 0,94738 | 0,94845 | 0,9495 | 0,95053 | 0,95154 | 0,95254 | 0,95352 | 0,95449 |
| 1,7 | 0,95543 | 0,95637 | 0,95728 | 0,95818 | 0,95907 | 0,95994 | 0,9608 | 0,96164 | 0,96246 | 0,96327 |
| 1,8 | 0,96407 | 0,96485 | 0,96562 | 0,96638 | 0,96712 | 0,96784 | 0,96856 | 0,96926 | 0,96995 | 0,97062 |
| 1,9 | 0,97128 | 0,97193 | 0,97257 | 0,9732 | 0,97381 | 0,97441 | 0,975 | 0,97558 | 0,97615 | 0,9767 |
| 2 | 0,97725 | 0,97778 | 0,97831 | 0,97882 | 0,97932 | 0,97982 | 0,9803 | 0,98077 | 0,98124 | 0,98169 |
| 2,1 | 0,98214 | 0,98257 | 0,983 | 0,98341 | 0,98382 | 0,98422 | 0,98461 | 0,985 | 0,98537 | 0,98574 |
| 2,2 | 0,9861 | 0,98645 | 0,98679 | 0,98713 | 0,98745 | 0,98778 | 0,98809 | 0,9884 | 0,9887 | 0,98899 |
| 2,3 | 0,98928 | 0,98956 | 0,98983 | 0,9901 | 0,99036 | 0,99061 | 0,99086 | 0,99111 | 0,99134 | 0,99158 |
| 2,4 | 0,9918 | 0,99202 | 0,99224 | 0,99245 | 0,99266 | 0,99286 | 0,99305 | 0,99324 | 0,99343 | 0,99361 |
| 2,5 | 0,99379 | 0,99396 | 0,99413 | 0,9943 | 0,99446 | 0,99461 | 0,99477 | 0,99492 | 0,99506 | 0,9952 |
| 2,6 | 0,99534 | 0,99547 | 0,9956 | 0,99573 | 0,99585 | 0,99598 | 0,99609 | 0,99621 | 0,99632 | 0,99643 |
| 2,7 | 0,99653 | 0,99664 | 0,99674 | 0,99683 | 0,99693 | 0,99702 | 0,99711 | 0,9972 | 0,99728 | 0,99736 |
| 2,8 | 0,99744 | 0,99752 | 0,9976 | 0,99767 | 0,99774 | 0,99781 | 0,99788 | 0,99795 | 0,99801 | 0,99807 |
| 2,9 | 0,99813 | 0,99819 | 0,99825 | 0,99831 | 0,99836 | 0,99841 | 0,99846 | 0,99851 | 0,99856 | 0,99861 |
| 3 | 0,99865 | 0,99869 | 0,99874 | 0,99878 | 0,99882 | 0,99886 | 0,99889 | 0,99893 | 0,99896 | 0,999 |
| 3,1 | 0,99903 | 0,99906 | 0,9991 | 0,99913 | 0,99916 | 0,99918 | 0,99921 | 0,99924 | 0,99926 | 0,99929 |
| 3,2 | 0,99931 | 0,99934 | 0,99936 | 0,99938 | 0,9994 | 0,99942 | 0,99944 | 0,99946 | 0,99948 | 0,9995 |
| 3,3 | 0,99952 | 0,99953 | 0,99955 | 0,99957 | 0,99958 | 0,9996 | 0,99961 | 0,99962 | 0,99964 | 0,99965 |
| 3,4 | 0,99966 | 0,99968 | 0,99969 | 0,9997 | 0,99971 | 0,99972 | 0,99973 | 0,99974 | 0,99975 | 0,99976 |
| 3,5 | 0,99977 | 0,99978 | 0,99978 | 0,99979 | 0,9998 | 0,99981 | 0,99981 | 0,99982 | 0,99983 | 0,99983 |
| 3,6 | 0,99984 | 0,99985 | 0,99985 | 0,99986 | 0,99986 | 0,99987 | 0,99987 | 0,99988 | 0,99988 | 0,99989 |
| 3,7 | 0,99989 | 0,9999 | 0,9999 | 0,9999 | 0,99991 | 0,99991 | 0,99992 | 0,99992 | 0,99992 | 0,99992 |
| 3,8 | 0,99993 | 0,99993 | 0,99993 | 0,99994 | 0,99994 | 0,99994 | 0,99994 | 0,99995 | 0,99995 | 0,99995 |
| 3,9 | 0,99995 | 0,99995 | 0,99996 | 0,99996 | 0,99996 | 0,99996 | 0,99996 | 0,99996 | 0,99997 | 0,99997 |
| 4 | 0,99997 | 0,99997 | 0,99997 | 0,99997 | 0,99997 | 0,99997 | 0,99998 | 0,99998 | 0,99998 | 0,99998 |

Somit wissen wir, dass der Läufer die Strecke von 100m mit einer Wahrscheinlichkeit von rund 9,2% in 11 bis 12 Sekunden bewältigt.


