Bedingte Wahrscheinlichkeit
Dieser Artikel beantwortet die Frage: „Was ist eine bedingte Wahrscheinlichkeit?“ und behandelt außerdem die Punkte bedingte Wahrscheinlichkeit Aufgaben und Beispiel.
Lange Texte lesen ist keine Bedingung dafür effektiv zu lernen. In diesem Video zeigen wir dir wie du die bedingte Wahrscheinlichkeiten berechnen kannst anhand eines einfachen Beispiels. Los geht’s!
Inhaltsübersicht
Bedingte Wahrscheinlichkeit Definition
Mit der bedingten Wahrscheinlichkeiten lässt sich die Wahrscheinlichkeit eines Ereignisses unter Bedingung des Eintritts eines anderen Ereignisses ausdrücken. Da die Berechnung erfordert, dass ein bestimmtes Ereignis schon eingetreten ist, wird diese auch konditionale Wahrscheinlichkeit genannt.
Bedingte Wahrscheinlichkeit Formel
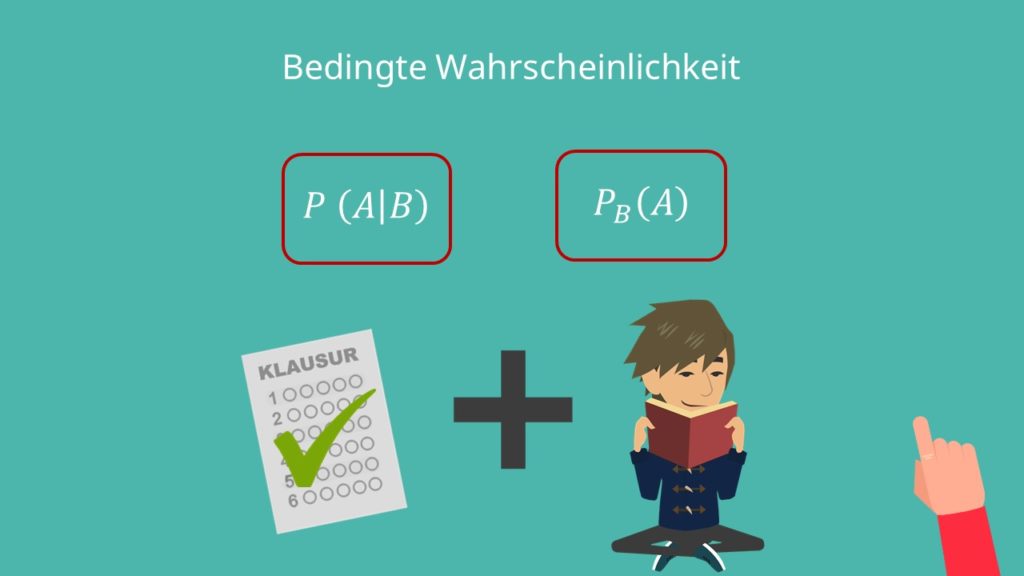
Beispielsweise lässt sich so die Wahrscheinlichkeit bestimmen, mit der du deine Klausuren bestehst, unter der Voraussetzung, dass du dafür gelernt hast. Es gibt verschiedene Schreibweisen für die bedingte Wahrscheinlichkeit. Die beiden häufigsten sind wohl diese:
Die Schreibweise drückt die Wahrscheinlichkeit für das Ereignis A aus unter der Voraussetzung, dass Ereignis B bereits eingetreten ist.
Die bedingte Wahrscheinlichkeit ist als Formel wie folgt definiert:
Bedingte Wahrscheinlichkeit Aufgaben
Zum besseren Verständnis erklären wir die bedingte Wahrscheinlichkeit anhand von konkreten Anwendungsfällen und dazugehörigen Aufgaben. Generell ist es das Ziel zu untersuchen, wie stark der statistische Einfluss einer Größe auf eine andere ist. Dazu kann man sich verschiedener Hilfsmittel bedienen, um den Sachverhalt strukturiert darstellen zu können.
Bedingte Wahrscheinlichkeit einfach erklärt
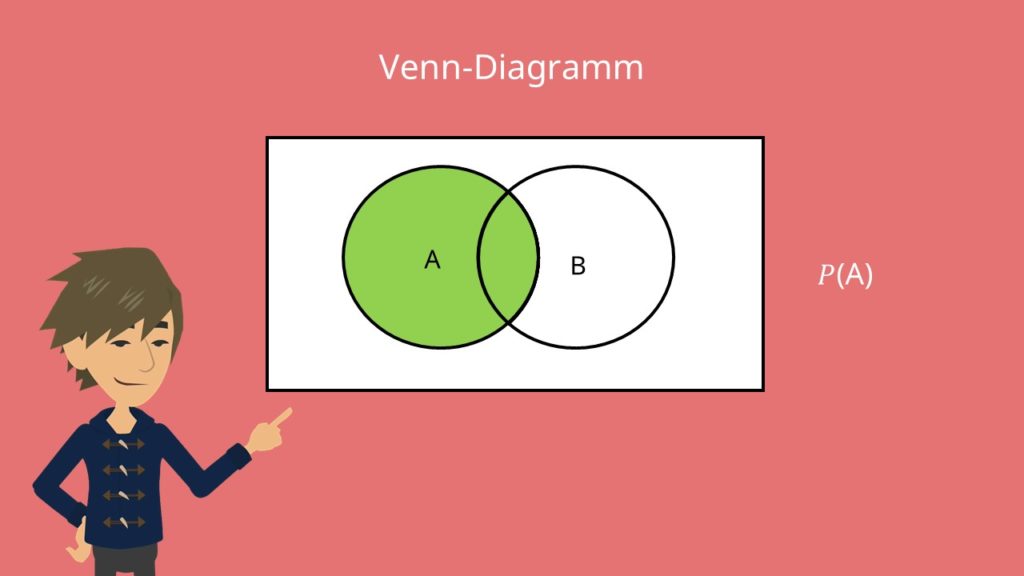
Am einfachsten lässt sich die bedingte Wahrscheinlichkeit anhand eines Venn Diagramms veranschaulichen. Zuerst einmal überlegen wir uns, wie wir die Wahrscheinlichkeit für das Ergebnis A ausdrücken können. Im Venn Diagramm sieht das so aus:
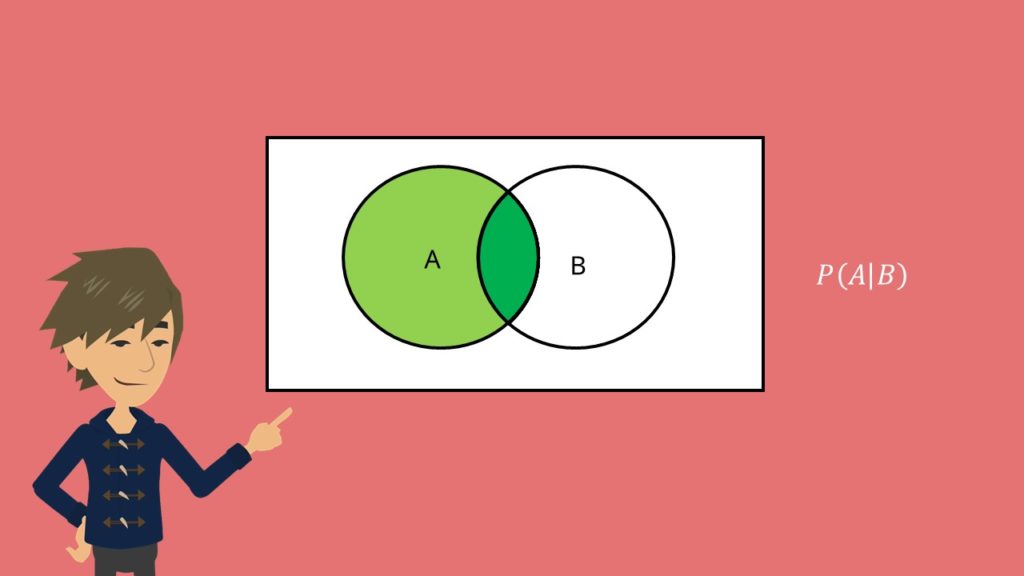
Wenn wir bereits wissen, dass Ereignis B eingetreten ist, verringert sich die mögliche Ergebnismenge auf die Schnittmenge aus A und B:
Bedingte Wahrscheinlichkeit Baumdiagramm
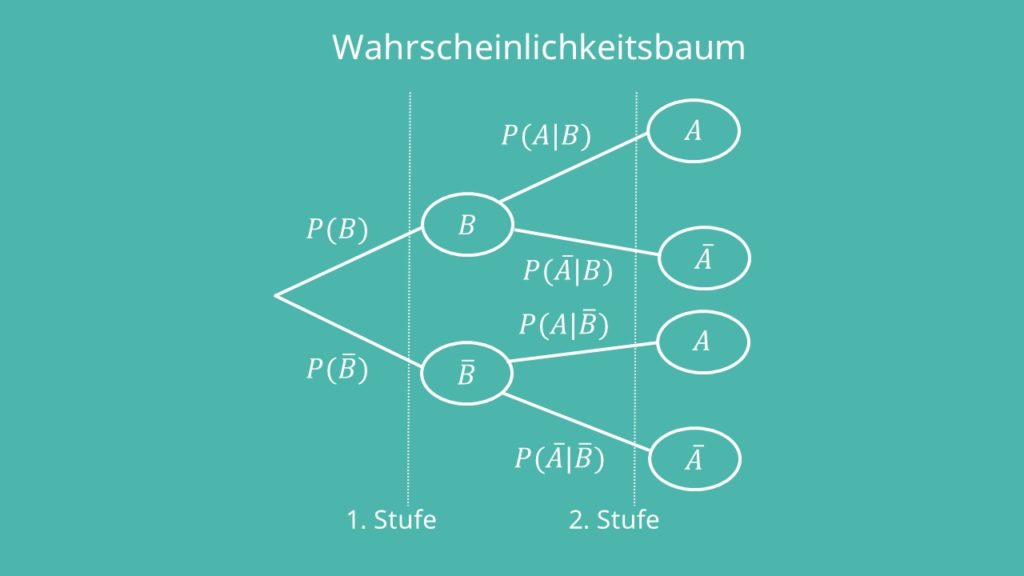
Eine weitere Möglichkeit, die bedingte Wahrscheinlichkeit darzustellen, ist in einem Baumdiagramm. Dazu haben wir wieder mindestens zwei Ereignisse A und B gegeben, die wir zusammen mit ihren Gegenwahrscheinlichkeiten als Wahrscheinlichkeitsbaum darstellen:
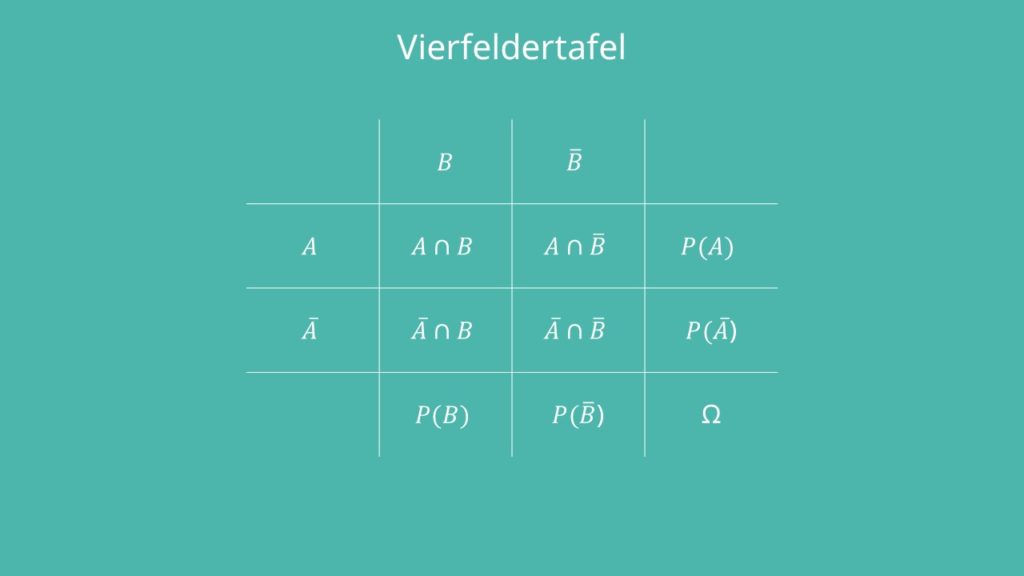
Bedingte Wahrscheinlichkeit Vierfeldertafel
Du kannst die bedingte Wahrscheinlichkeit sogar einer Vierfeldertafel entnehmen. Die fertig ausgefüllte Tafel würde dann so aussehen:
Um nun beispielsweise die bedingte Wahrscheinlichkeit von B unter der Bedingung des Eintritts von A zu ermitteln, musst du einfach folgendes berechnen:

Bedingte Wahrscheinlichkeit berechnen
Schauen wir uns abschließend noch ein passendes Beispiel dazu an. Stell dir vor, du wirfst einen Würfel. Die Ergebnismenge A beinhaltet alle geraden Zahlen und die Ergebnismenge B beinhaltet alle Zahlen von 4 bis 6.


Jetzt sollst du die Wahrscheinlichkeit für A berechnen, unter der Bedingung, dass B bereits eingetreten ist. Um unsere Formel von vorhin verwenden zu können, müssen wir erst die Wahrscheinlichkeit für Ergebnis B berechnen. Da drei Elemente in der Menge B enthalten sind und der Würfel sechs Seiten hat, ist die Wahrscheinlichkeit für B gleich 0,5.

Als nächstes müssen wir noch die Wahrscheinlichkeit für A geschnitten B berechnen, also für die Ergebnisse, die in A und in B enthalten sind. Da die Menge A geschnitten B genau 2 Elemente enthält, nämlich 4 und 6, beträgt die Wahrscheinlichkeit hierfür 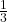 .
.


Jetzt können wir alles in die Formel einsetzen und erhalten so eine Wahrscheinlichkeit in Höhe von 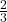 .
.
Stochastik Bedingte Wahrscheinlichkeit
In der Stochastik wird versucht die Wahrscheinlichkeiten für alle möglichen Szenarien zu berechnen. Um dies zu ermöglichen gibt Vielzahl an Sätzen und Formeln, welche die geforderten Bedingungen umsetzten. Die wichtigsten, welche dir in Verbindung mit der bedingten Wahrscheinlichkeit begegnen können, stellen dir im Folgenden kurz vor.
Bedingte Wahrscheinlichkeit Unabhängigkeit
Weiß man, dass zwei Ereignisse stochastisch unabhängig voneinander sind, dann kann auch logischerweise die Formel für die bedingte Wahrscheinlichkeit nicht mehr Anwendung finden.
 vereinfacht sich zu
vereinfacht sich zu  . Dann gilt für die bedingte Wahrscheinlichkeit für den Eintritt des Ereignisses A:
. Dann gilt für die bedingte Wahrscheinlichkeit für den Eintritt des Ereignisses A:

Wenn du das Thema genauer verstehen willst, kannst du dir unser Video zur stochastischen Unabhängigkeit von Ereignissen ansehen.
Multiplikationssatz und Gegenwahrscheinlichkeit
Du kennst nun die Formel zur bedingten Wahrscheinlichkeit und kannst dich wahrscheinlich noch an die Pfadregeln zum Baumdiagramm erinnern. Mithilfe dieser Regeln lassen sich andere Sätze herleiten, die du dir auf jeden Fall einprägen solltest:
Multiplikationssatz: 
Mit dem Multiplikationssatz wird die Wahrscheinlichkeit berechnet, dass zwei Ereignisse eintreten werden. Wie man erkennen kann, ist die Formel sehr ähnlich zu der der bedingten Wahrscheinlichkeit.
Gegenwahrscheinlichkeit: 
Die Gegenwahrscheinlichkeit ist die Wahrscheinlichkeit, dass das Gegenteil des betrachteten Ereignisses eintritt. Deshalb ergibt sich aus der Summe der Wahrscheinlichkeiten des Ereignisses 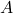 und dessen Gegenereignis
und dessen Gegenereignis 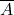 immer 1 oder eben 100%.
immer 1 oder eben 100%.
Zwei weitere sehr wichtige Sätze, welche dir in Verbindung mit der bedingten Wahrscheinlichkeit begegnen können sind außerdem der Satz der totalen Wahrscheinlichkeit und der Satz von Bayes . Zu diesen Sätzen haben wir seperate Videos, welche dir die Themen anschaulich erklären.
Das wars auch schon zur bedingten Wahrscheinlichkeit! Zur Wiederholung findest du hier nochmal die zentrale Formel: